이 페이지에서는 단항식의 부분(계수, 문자 부분, 차수 등)이 무엇인지, 그리고 이를 쉽게 식별하는 방법을 설명합니다. 또한 단항식 부분에 대해 단계별로 예제를 보고 연습을 통해 연습할 수도 있습니다.
단항식의 부분은 무엇입니까?
단항식의 부분은 다음과 같습니다:
- 계수 : 단항식의 변수(또는 문자)를 곱하는 숫자입니다.
- 변수 : 단항식에 나타나는 각 문자입니다.
- 리터럴 부분 : 모든 지수로 단항식을 형성하는 모든 변수에 해당합니다.
- Degree : 단항변수의 모든 지수의 합입니다.
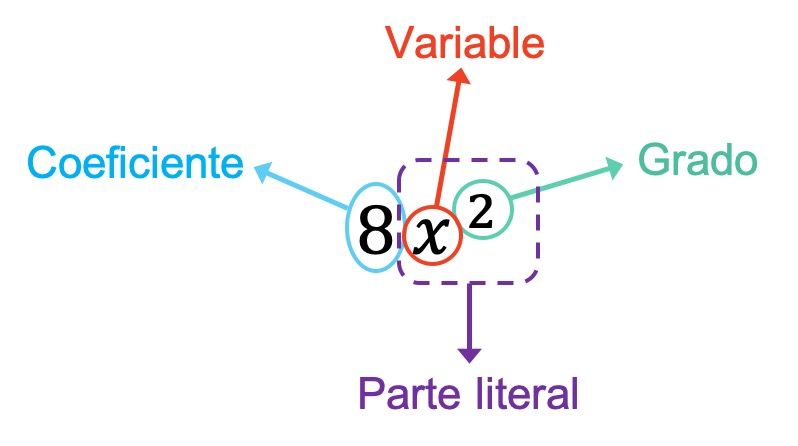
이전 예에서 볼 수 있듯이 단항식의 계수는 변수를 곱하는 숫자이므로 8입니다. 또한 이 경우 단항식에는 x라는 변수가 하나만 있습니다. 따라서 단항식의 문자 부분은 이 변수에 지수(예: x 2 ) 를 더한 값으로 구성됩니다. 그리고 마지막으로 단항식은 유일한 지수가 2이기 때문에 2차입니다.
반면, 단항식 부분의 속성 중 하나는 두 단항식의 문자 부분이 동일한 경우 이를 유사한 단항식 이라고 합니다. 링크된 페이지에서 이러한 유형의 단항식에 대해 자세히 알아볼 수 있으며, 무엇보다도 단항식이 수학에 중요한 이유가 설명되어 있습니다.
단항식의 일부 예
단항식 부분의 개념을 완전히 이해할 수 있도록 몇 가지 예를 제시합니다.
실시예 1
![]()
- 단항식의 계수:
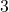
- 단항변수:
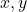
(이 경우에는 두 가지 변수가 있습니다)
- 단항식의 문자적 부분:
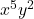
- 단항식의 차수:
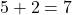
실시예 2
![]()
- 단항식의 계수:
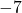
- 단항변수:
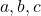
(이 경우에는 세 가지 변수가 있습니다)
- 단항식의 문자적 부분:
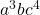
- 단항식의 차수:
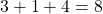
변수의 지수가 설정되지 않은 경우 이는 변수가 1로 증가한다는 의미이므로 실제로 해당 변수의 지수는 0이 아닌 1입니다. 이러한 이유로 우리는 계산에 단위를 추가했습니다. 이 단항식의 차수(3+ 1 +4=8), 왜냐하면
![]()
더 관심이 있으시면 다음 링크에서 단항식의 더 많은 예를 볼 수 있습니다. 또한 존재하는 다양한 유형의 단항식, 단항식의 수치 계산 방법, 단항식과 다항식의 차이점을 확인할 수 있습니다.
단항식 부분의 문제 해결
마지막으로, 단항식 부분의 다양한 정의를 이해했는지 확인할 수 있도록 몇 가지 연습을 제공합니다.
연습 1
다음 단항식의 부분은 모두 무엇입니까?
![]()
단항식의 계수:
![]()
단항변수:
![]()
단항식의 문자적 부분:
![]()
단항식의 차수:
![]()
연습 2
다음 단항식의 모든 요소를 식별하십시오.
![]()
단항식의 계수:
![]()
단항변수:
![]()
단항식의 문자적 부분:
![]()
단항식의 차수:
![]()
연습 3
분수를 사용하여 다음 단항식의 부분을 결정합니다.
![]()
단항식의 계수:
![]()
단항변수:
![]()
단항식의 문자적 부분:
![]()
단항식의 차수:
![]()
완벽한! 지금까지 해냈다면 아마도 이미 단항식의 부분에 대한 모든 것을 이해했을 것입니다. 이것이 바로 여러분이 다음 단계로 나아가서 단항식을 사용하여 연산을 수행하는 방법을 배울 준비가 된 이유입니다. 여기에서는 존재하는 모든 유형의 단항식 연산이 어떻게 계산되는지 볼 수 있을 뿐만 아니라 단항식과 결합된 연산을 해결하는 방법도 볼 수 있으며 해결 연습을 단계별로 연습할 수 있습니다.