이 페이지에서는 동일 평면 벡터가 무엇인지, 그리고 2, 3, 4개 이상의 벡터가 동일 평면에 있는지 확인하는 방법을 배웁니다. 또한 동일 평면 벡터에 대해 단계별로 해결되는 예제와 연습을 볼 수 있습니다.
동일 평면 벡터란 무엇입니까?
해석 기하학에서 동일 평면(또는 동일 평면) 벡터의 의미는 다음과 같습니다.
동일 평면 벡터는 동일한 평면에 속하는 벡터입니다.
따라서 평면은 최소 2개의 벡터로 구성될 수 있으므로 두 벡터는 항상 동일 평면에 있습니다. 반면에 3, 4개 이상의 벡터가 있는 경우 벡터 중 하나가 동일한 평면에 포함되지 않아 동일 평면에 있지 않을 수 있습니다.
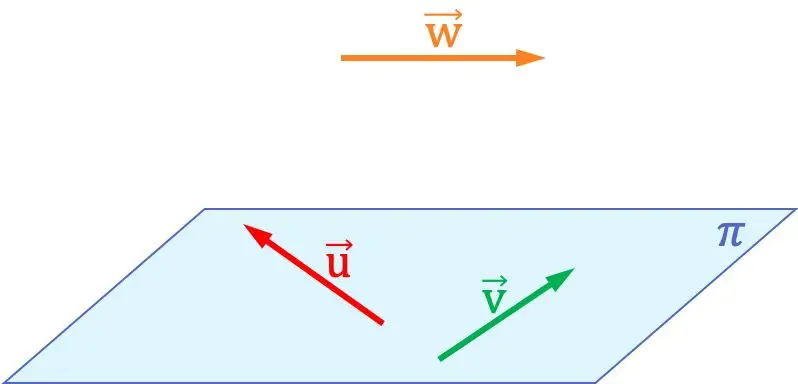
예를 들어, 위 그래프에서 벡터는 다음과 같습니다.
![]()
그리고
![]()
그들은 같은 평면에 포함되어 있기 때문에 서로 동일 평면에 있습니다. 반면에, 이 두 벡터는 벡터와 동일 평면에 있지 않습니다.
![]()
, 세 개의 벡터를 포함하는 공간에서는 평면을 형성할 수 없기 때문입니다.
이 속성으로부터 우리는 3개 이상의 벡터가 동일 평면에 있는 경우 해당 벡터를 정의하는 점(벡터의 시작과 끝)도 동일 평면에 있는 점이라고 추론할 수 있습니다.
벡터는 언제 동일 평면상에 있나요?
동일 평면(또는 동일 평면) 벡터의 정의에서 보았듯이 두 벡터는 항상 동일 평면에 있지만 두 개 이상의 벡터가 동일 평면 관계를 준수할 필요는 없습니다.
따라서 3개 이상의 벡터가 동일 평면에 있는지 확인하는 방법에는 여러 가지가 있습니다.
- 세 벡터의 혼합 곱(또는 삼중 내적)이 0이면 세 벡터가 동일 평면에 있다는 의미입니다. 이 연산이 어떻게 계산되는지 명확하지 않은 경우 세 벡터의 혼합 곱이 무엇인지 살펴보는 것이 좋습니다. 여기에서 설명과 예제 및 해결된 연습 문제를 찾을 수 있습니다.
![]()
- 벡터 집합이 두 벡터의 선형 결합 으로 표현될 수 있는 경우 이는 해당 벡터가 동일 평면에 있음을 의미합니다. 즉, 3개 이상의 벡터가 선형 종속인 경우에만 동일 평면에 있음을 의미합니다. 3개 이상의 벡터가 두 벡터의 선형결합임을 보여주기 위해서는 모든 벡터로 구성된 행렬의 랭크가 2이면 충분합니다.
![]()
선형 의존성과 독립성 의 개념, 즉 두 벡터가 선형 종속 또는 선형 독립인 경우와 그 의미를 잘 이해하는 것이 중요합니다. 완전히 명확하지 않은 경우 링크에서 매우 자세한 설명을 찾을 수 있으며, 또한 단계별로 해결되는 예제와 연습도 볼 수 있습니다.
- 문제의 벡터가 평행 벡터 인 경우 이는 해당 벡터도 동일 평면에 있음을 의미합니다. 즉, 모든 평행 벡터가 동일한 평면에 포함되어 있음을 의미합니다.
![]()
동일 평면 벡터의 문제 해결
연습 1
다음 세 벡터가 동일 평면에 있는지 확인합니다.
![]()
![]()
![]()
이것이 3개의 동일 평면 벡터인지 확인하려면 세 벡터 간의 혼합 곱을 계산해야 합니다.
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 3 & -1 \\[1.1ex] -1 & -5 & 4 \end{vmatrix} \\[2ex] &= 36+1-20+6-15-8 \\[2ex] & = \bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a1e4b0655c0a3f0165c880f5e64cce0_l3.png)
세 벡터의 혼합 곱은 0이므로 세 벡터는 동일 평면에 있습니다 .
연습 2
다음 세 벡터가 동일 평면에 있는지 확인합니다.
![]()
![]()
![]()
3개의 동일 평면 벡터를 다루고 있는지 확인하는 한 가지 방법은 세 벡터 간의 혼합 곱을 푸는 것입니다. 그러나 벡터의 구성요소를 자세히 살펴보면 비례한다는 것을 알 수 있습니다. 따라서 세 벡터는 서로 평행하다.
![]()
그리고 모든 벡터가 평행하므로 사실상 3개의 동일 평면 벡터입니다 .
연습 3
다음 네 벡터가 동일 평면에 있는지 확인합니다.
![]()
![]()
![]()
![]()
4개의 벡터가 동일 평면에 있는지 확인하려면 모든 벡터로 구성된 행렬의 순위를 계산해야 합니다.
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8384924c86edafd568505d5f80e1705d_l3.png)
이 경우 행렬식으로 해당 행렬의 범위를 계산합니다.
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex] -1&0&-1 \end{vmatrix}=0 \quad \begin{vmatrix} 2&1&1 \\[1.1ex] 1&-1&2 \\[1.1ex]3&1&2\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-2778435c7f53952adf072419af8b268c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&1 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0 \quad \begin{vmatrix} 1&-1&2 \\[1.1ex] -1&0&-1 \\[1.1ex] 3&1&2\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-82f278494a221879cc86da92ab4378c8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1 \\[1.1ex] 1&-1\end{vmatrix}= -3\neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-889142ac348173dd6c838633007f2d06_l3.png)
![]()
모든 벡터로 구성된 행렬의 순위는 2와 동일하므로 4개의 벡터는 동일 평면에 있습니다 .
연습 4
매개변수 값 계산
![]()
따라서 다음 4개의 점이 동일 평면상에 있습니다.
![]()
![]()
![]()
![]()
4개의 점이 동일 평면에 있으려면 해당 점에 의해 결정된 벡터가 동일 평면에 있어야 합니다. 따라서 우리는 다음 벡터를 계산합니다.
![]()
![]()
![]()
벡터 행렬은 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c3d801efcf5b56dd858890720797d6a4_l3.png)
결과 벡터가 동일 평면이 되려면 행렬의 순위가 2여야 합니다. 따라서 전체 3×3 행렬의 행렬식은 0이어야 합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1&0&-2 \\[1.1ex] -3&-2&-1 \\[1.1ex] 0&1&k-4\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-bb7d3b31c10096d100843d781a85b621_l3.png)
![]()
마지막으로 미지의 문제를 해결합니다.
![]()
![]()
![]()