이 페이지에서는 원뿔곡선의 정의, 이것이 왜 그렇게 중요한지, 그리고 존재하는 원뿔곡선의 다양한 유형(원, 타원, 쌍곡선 및 포물선)을 찾을 수 있습니다. 또한 방정식 간의 차이점을 확인할 수 있습니다.
원뿔 단면이란 무엇입니까?
분석 기하학에서 원뿔 단면(또는 간단히 원뿔)은 원뿔과 평면 사이의 다양한 교차점에서 발생하는 모든 곡선입니다. 이 평면은 원뿔의 꼭지점을 통과하지 않습니다. 원뿔 단면에는 원, 타원, 포물선, 쌍곡선의 네 가지 유형이 있습니다.
다음은 모든 원뿔에서 얻을 수 있는 4가지 섹션입니다.
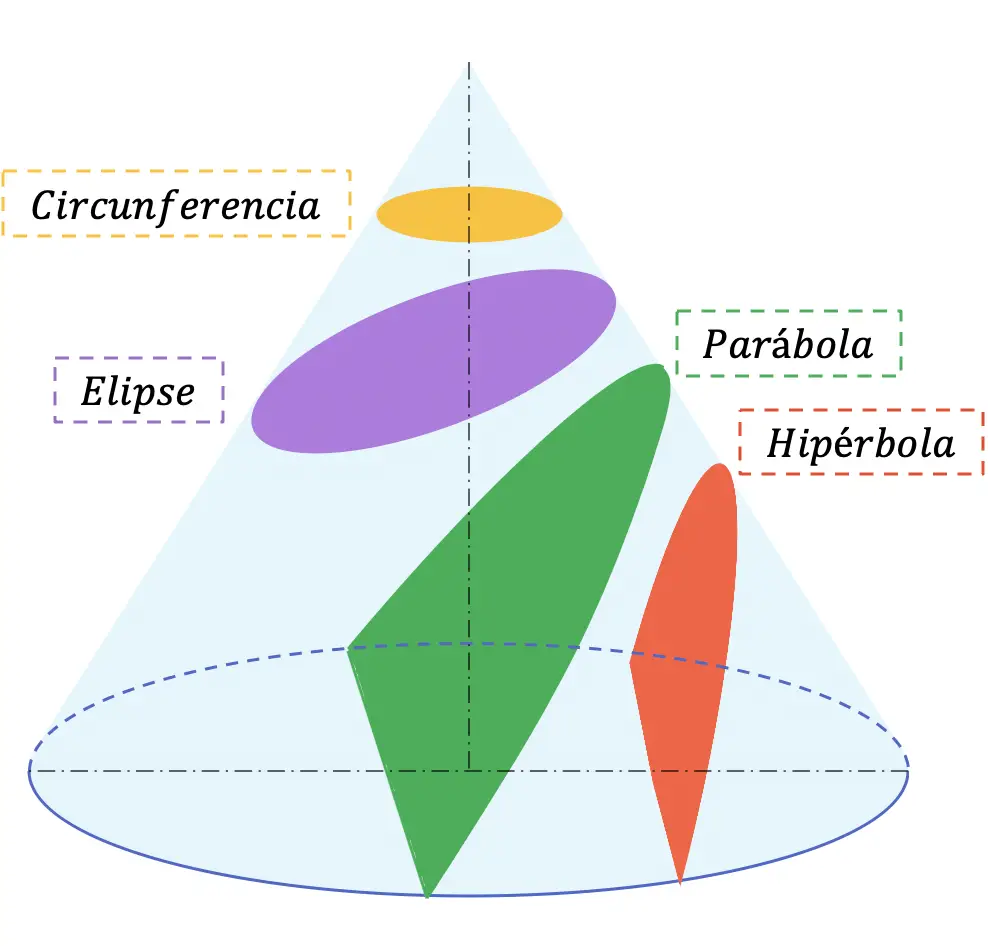
원뿔 단면은 일반적으로 중등학교(Bachillerato)에서 수학과 기술 도면 과목을 공부합니다.
원추형 단면의 유형
원뿔곡선의 개념을 살펴보았다면, 원뿔곡선, 타원곡선, 포물선, 쌍곡선의 네 가지 유형의 원뿔곡선이 무엇인지 살펴보겠습니다.
둘레
원주는 회전축에 수직인 평면(베이스에 평행한)으로 원뿔을 절단하여 찾을 수 있는 원추형 단면입니다.

또한, 원주는 중심이라고 불리는 고정된 점으로부터 등거리에 있는 평면 위의 점들의 궤적입니다.
타원
타원은 원주와 매우 유사한 평평하고 닫힌 곡선이지만 모양은 더 타원형입니다. 특히 회전축에 대한 각도가 발전기의 각도보다 큰 경사면으로 원뿔 표면을 절단한 결과입니다.
또한, 타원의 모든 점은 조건을 충족합니다. 타원은 두 개의 다른 고정된 점(초점 F 및 F’라고 함)까지의 거리의 합이 일정한 평면의 모든 점의 궤적입니다.

우화
수학에서 포물선은 고정점(초점이라고 함)과 고정선(준선이라고 함)으로부터 등거리에 있는 평면 위의 점들의 궤적입니다.

기하학적으로 포물선은 원뿔 모선의 각도와 동일한 회전축에 대한 경사각을 갖는 평면에 의한 원뿔 단면의 결과입니다. 따라서 포물선을 포함하는 평면은 원뿔 생성기와 평행합니다.
이 원뿔 단면의 매우 중요한 특징은 포물선 방정식 입니다. 왜냐하면 상태에 따라 포물선의 유형을 식별할 수 있기 때문입니다. 이 링크에서는 포물선의 모든 방정식, 포물선의 요소, 속성, 예, 풀이 연습 등 포물선의 다른 특성을 찾을 수 있습니다.
쌍곡선
원뿔 단면으로서 쌍곡선은 원뿔의 회전축을 기준으로 원뿔 생성기에 의해 형성된 각도보다 작은 각도로 평면으로 원뿔을 자르면 얻어집니다.
수학적으로 쌍곡선은 다음 속성을 충족하는 평면 위 점의 궤적으로 정의할 수 있습니다. 쌍곡선 위의 한 점과 두 고정점(초점이라고 함) 사이의 거리 차이의 절대값은 일정해야 합니다.
더욱이, 이 두 거리를 뺀 값은 항상 쌍곡선의 두 꼭지점 사이의 거리와 동일합니다.
![]()

당신이 이미 추론했다고 확신하는 것처럼, 매개변수 값은
![]()
쌍곡선의 기본은 쌍곡선의 기본입니다. 다음 링크에서 쌍곡선에 대한 설명을 볼 수 있습니다. 여기서 쌍곡선을 특징짓는 모든 요소는 물론 이것이 그렇게 중요한 계수인 이유를 확인할 수 있습니다. 또한 쌍곡선의 방정식이 어떻게 생겼는지, 존재하는 다양한 유형의 쌍곡선, 심지어 쌍곡선에 대한 단계별 문제와 연습 문제까지 알아볼 수 있습니다.
원뿔 단면의 일반 방정식
각 원뿔 단면은 방정식으로 해석적으로 표현될 수 있습니다. 실제로 모든 원뿔 방정식은 2차 방정식이어야 합니다.
![]()
결과적으로, 계수 중 적어도 하나는
![]()
어느 하나
![]()
수식의 값은 0이 아니어야 합니다.
따라서 매개변수 값에 따라 방정식은 원뿔형 또는 다른 유형에 해당합니다.
- 원주 : 원주를 설명하는 일반 방정식의 경우 다음 용어가 사용됩니다.

그리고

일치해야 하며

0이어야 합니다.
![]()
- Ellipse : 방정식은 다음 조건이 확인될 때 타원의 수학적 표현에 해당합니다.
![]()
- 포물선 : 방정식이 포물선이 되려면 다음 등식을 충족해야 합니다.
![]()
- 쌍곡선 : 마지막으로, 쌍곡선의 일반 방정식은 다음 부등식을 만족해야 합니다:
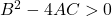 글 탐색
글 탐색