타원의 이심률 계산

이 페이지에서는 타원의 이심률의 의미와 계산 방법(공식)을 확인할 수 있습니다. 또한 타원 편심 계산의 예도 볼 수 있습니다.

타원의 이심률은 얼마입니까?

타원 이심률은 타원이 얼마나 둥글거나 평평한지를 측정하는 매개변수입니다. 즉, 타원의 이심률은 타원이 원과 얼마나 유사한지를 나타냅니다.

다른 한편으로, 타원이 무엇으로 구성되어 있는지 생각해 봅시다. 타원은 두 개의 다른 고정된 점(초점 F 및 F’라고 함)까지의 거리의 합이 일정한 평면의 모든 점의 궤적 입니다.

타원 이심률 공식

타원의 이심률에 대한 정의를 확인한 후 공식을 통해 이심률이 어떻게 계산되는지 살펴보겠습니다.

타원의 이심률 공식은 다음과 같습니다.

$e=\cfrac{c}{a}$

금:

$e$

타원의 이심률이다
$c$

타원의 초점(점 F 및 F’)에서 중심까지의 거리입니다.
$a$

타원의 장반(또는 장축) 축의 길이입니다.

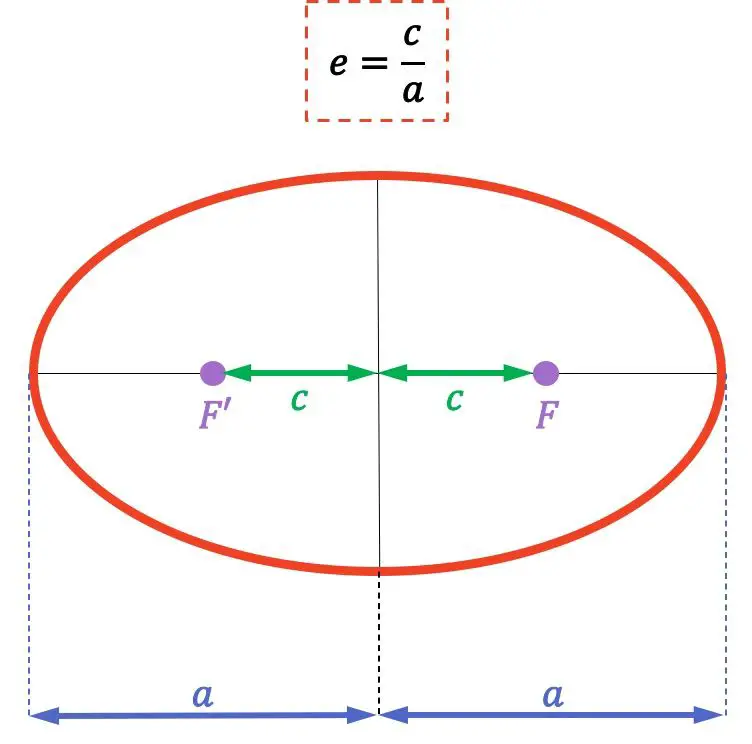
타원의 초점은 타원 위의 한 점까지의 거리의 합이 일정한 고정된 점이라는 점을 기억하십시오. 또한 두 초점 사이의 거리를 초점 거리라고 합니다.

이심률 값의 범위는 0(완벽한 원)부터 1(수평선)까지입니다. 분명히 결과 기하학적 개체가 더 이상 타원이 아니기 때문에 0과 1은 포함되지 않습니다.

$0 Par conséquent, comme vous pouvez le voir dans la représentation graphique ci-dessous, plus la valeur de l'excentricité de l'ellipse est petite, plus elle ressemble à un cercle, au contraire, plus le coefficient est grand, plus l'ellipse est aplatie. <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="https://mathority.org/wp-content/uploads/2023/07/excentricite-dellipse.webp" alt="valeur de l'excentricité de l'ellipse" class="wp-image-2095" width="669" height="154" srcset="" sizes=""></figure> </div> <p> En bref, l’excentricité d’une ellipse est un coefficient dont la valeur détermine la forme qu’elle a. </p> <div class="adsb30" style=" margin:12px; text-align:center"> <div id="ezoic-pub-ad-placeholder-109"></div> </div> <p> Si vous êtes plus intéressé par les caractéristiques d’une ellipse, vous pouvez vous référer à l’ <a href="https://mathority.org/equation-de-la-formule-de-l'ellipse/">équation de l’ellipse</a> . Sur cette page, vous trouverez une explication détaillée de ce qu’est une ellipse, de tous ses éléments et de la façon dont son équation est calculée. Et, en plus, vous pourrez voir plusieurs exemples, exercices et problèmes résolus sur des ellipses. </p> <h2 class="wp-block-heading"><span class="ez-toc-section" id="relacion-importante-para-hallar-la-excentricidad-de-la-elipse"></span> Relation importante pour trouver l’excentricité de l’ellipse<span class="ez-toc-section-end"></span></h2> <p> Les différents éléments d’une ellipse sont liés les uns aux autres. De plus, les relations entre eux sont très importantes pour les exercices sur les ellipses, car elles sont généralement nécessaires pour résoudre des problèmes sur les ellipses et déterminer leurs équations. Comme nous l’avons vu plus haut dans l’explication de la notion d’excentricité de l’ellipse, la distance de tout point de l’ellipse au foyer F plus la distance du même point au foyer F’ est constante. Eh bien, cette valeur constante est égale à deux fois ce que mesure le demi-grand axe. Autrement dit, l’égalité suivante vaut pour tout point d’une ellipse :” title=”Rendered by QuickLaTeX.com” height=”478″ width=”3899″ style=”vertical-align: -4px;”></p> <p> d(P,F) + d(P,F’)= 2a</p> <p class=$ $Où$

d(P,F)

$et$

d(P,F’)

$est la distance du point P au foyer F et F' respectivement et$

가지다

$est la longueur de l'axe semi-focal. Par conséquent, puisque le sommet de l'axe secondaire est juste au milieu de l'axe principal, la distance de celui-ci à l'un des foyers est équivalente à la longueur du demi-axe principal ($

가지다

$): <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="https://mathority.org/wp-content/uploads/2023/07/relation-delements-dellipse.webp" alt="équation de preuve d'ellipse" class="wp-image-2087" width="332" height="197" srcset="" sizes=""></figure> </div> <p> Par conséquent, à partir du théorème de Pythagore, il est possible de trouver <strong>la relation qui existe entre le demi-axe principal, le demi-axe secondaire et la distance semi-focale d’une ellipse :</strong>” title=”Rendered by QuickLaTeX.com” height=”195″ width=”582″ style=”vertical-align: -5px;”></p> <p> a^2=b^2+c^2</p> <p class=$ $Retenez également cette autre formule car elle vous sera très utile pour calculer le résultat des exercices avec des ellipses. <h2 class="wp-block-heading"><span class="ez-toc-section" id="ejemplo-de-como-calcular-la-excentricidad-de-la-elipse"></span> Exemple de calcul de l’excentricité de l’ellipse<span class="ez-toc-section-end"></span></h2> <p> Vous trouverez ci-dessous un exercice résolu pour voir comment l’excentricité d’une ellipse est calculée :</p> <ul> <li> Trouver l’excentricité de l’ellipse dont le demi-grand axe et le demi-grand axe mesurent respectivement 5 et 3 unités.</li> </ul> <p> Pour trouver la valeur de l’excentricité de l’ellipse, il faut connaître la longueur du demi-axe principal et la longueur du segment entre un foyer et le centre de l’ellipse. Nous connaissons déjà le premier, nous n’avons donc qu’à déterminer la distance semi-focale. A partir de la formule de la relation entre les éléments d’une ellipse, on peut calculer combien vaut la demi-distance focale : ” title=”Rendered by QuickLaTeX.com” height=”193″ width=”2952″ style=”vertical-align: -5px;”></p> <p> a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{5^2-3^2}=\sqrt {16} = 4</p> <p class=$ $Et quand on connaît déjà la valeur des termes$