이 페이지에서는 원주 방정식에 관한 모든 것을 찾을 수 있습니다: 일반 방정식, 일반 방정식, 기타 유형의 원주 방정식, 원주 방정식이 올바른 경우… 또한 원주 방정식을 찾는 방법의 예도 볼 수 있습니다. 원주방정식을 풀어 연습문제를 풀어볼 수 있습니다.
원의 일반 방정식
원주 방정식이 무엇인지 알아보기 전에 원주의 개념을 떠올려 보겠습니다.
원주는 중심이라고 불리는 고정된 점으로부터 등거리에 있는 평면 위의 점들의 궤적입니다.

따라서 원 위의 모든 점은 중심으로부터의 거리가 같습니다.
또한 원은 타원, 포물선, 쌍곡선과 함께 4개의 원뿔 단면 중 하나입니다. 즉, 밑면과 평행한 평면으로 원뿔을 자르면 원을 얻을 수 있습니다.
데카르트 평면의 원을 설명하는 가장 간단한 방법은 일반 방정식을 이용하는 것입니다. 따라서 일반 원주 방정식의 공식은 다음과 같습니다.
원의 일반 방정식은 다음과 같습니다.
![]()
금:
-

원의 반지름입니다.
-

그리고

는 원 중심의 좌표입니다.
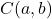
조금 지루해서 보여주지는 않겠지만, 이 방정식은 피타고라스의 정리로부터 얻을 수 있습니다.
예를 들어 원의 일반 방정식이 어떻게 계산되는지 살펴보겠습니다.
- 중심이 점인 반지름이 5인 원의 일반 방정식을 구합니다.
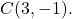
원의 일반 방정식의 공식은 다음과 같습니다.
![]()
그러므로 우리는 미지의 것을 대체해야만 한다.
![]()
반경의 값과 미지의 값으로
![]()
그리고
![]()
원 중심의 각각 X와 Y 좌표로:
![]()
따라서 원의 일반 방정식은 다음과 같습니다.
![]()
원의 일반 방정식
원주 방정식의 또 다른 유형은 일반 방정식으로, 실제로 가장 많이 사용됩니다. 그런 다음 일반 방정식에서 원주의 일반 방정식을 얻는 방법을 살펴보겠습니다.
원의 일반 방정식을 생각해 보세요.
![]()
우리가 놀라운 동등성(또는 놀라운 제품)을 개발한다면:
![]()
![]()
이제 변수를 3가지 변경합니다.
![]()
그리고 마지막으로 원주의 일반 방정식을 얻습니다.
![]()
따라서 원주 일반 방정식 의 공식은 다음과 같습니다.
![]()
원의 중심은 다음과 같습니다.
![]()
그리고 원의 반지름은 다음과 같습니다.
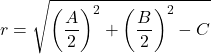
따라서 이 원주 방정식은 항상 일반 방정식으로 구해집니다. 다음은 수행 방법을 보여주는 예입니다.
- 중심이 점인 반지름이 6인 원의 일반 방정식을 결정합니다.
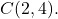
먼저 우리는 원의 일반 방정식을 찾아야 합니다. 이를 위해 우리는 그의 공식을 사용합니다:
![]()
![]()
이제 우리는 원주의 일반 방정식을 찾을 때까지, 즉 더 이상 단순화할 수 없을 때까지 작업합니다.
![]()
![]()
![]()
![]()
따라서 원의 일반 방정식은 다음과 같습니다.
![]()
문제에서는 이를 필요로 하지 않았지만 이제 찾은 방정식의 중심과 반경을 계산하여 그것이 올바른지 확인할 수 있습니다.
원의 중심을 결정하기 위해 다음 공식을 사용합니다.
![]()
![]()
![]()
![]()
실제로 원의 중심은 진술의 중심과 일치합니다.
또한 공식을 사용하여 원주 반경을 확인합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04dc99d462a8ceb5e6dca936999a4ce8_l3.png)
그리고 반경도 진술의 반경과 같습니다. 따라서 계산된 원주 방정식이 정확합니다.
둘레의 존재
모든 방정식은 다음과 같습니다.
![]()
원에 해당합니다. 따라서 이러한 유형의 표현이 진정한 원의 방정식이 되려면 다음 3가지 조건을 충족해야 합니다.
- 계수
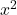
그리고
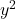
그들은 1과 같아야 합니다. 두 변수 앞에 1이 아닌 다른 숫자가 있지만 둘 다 같은 숫자인 경우 전체 방정식을 해당 숫자로 나누어 계수가 1이 될 수 있다는 점을 명심하십시오.
- 방정식에는 항이 있을 수 없습니다.
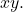
- 다음 표현식은 양수여야 합니다.
 다른 유형의 원 방정식
다른 유형의 원 방정식
지금까지 살펴본 두 개의 원 방정식, 즉 일반 방정식과 일반 방정식은 평면(R2)에서 원을 수학적으로 표현하는 데 가장 많이 사용됩니다. 그러나 이 기하학적 객체를 설명하는 방정식에는 여러 유형이 있으며, 아래에서는 각각에 대한 설명을 제공합니다.
원의 정식 방정식
원의 표준 방정식 또는 축소 방정식 은 중심이 좌표의 원점, 즉 점(0,0)에 있는 원을 설명하는 데 사용됩니다. 해당 방정식은 다음과 같습니다.
![]()
또한 반지름이 단위 (1)과 동일하다면 원주 방정식은 다음과 같습니다.
![]()
이 마지막 방정식은 단위 원주 또는 단위 원이라고도 하는 각도 측정 원주에 해당합니다. 좌표의 원점을 중심으로 하는 반지름 1의 원입니다.
두 동심원의 방정식
두 개의 동심방정식은 중심이 같은 점에 있는 방정식입니다. 그리고 두 개의 동심원이 갖는 유일한 차이점은 반지름입니다.
따라서 이 조건이 충족되려면 두 동심원의 방정식은 서로 달라야 하는 독립 항을 제외하고는 완전히 동일합니다.
![]()
![]()
예를 들어, 다음 두 원은 독립 항을 제외하고 모든 계수가 동일하므로 동심원입니다.
![]()
![]()
원의 매개변수 방정식
선과 마찬가지로 원의 방정식도 사인과 코사인의 삼각 함수를 사용하여 매개변수화할 수 있습니다. 따라서 원의 매개변수 방정식은 다음과 같습니다.
![Rendered by QuickLaTeX.com \diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)](https://mathority.org/wp-content/ql-cache/quicklatex.com-72dae5b3c5f775661ecb102945bb3fbd_l3.png)
요점은 어디인가
![]()
원의 중심이고
![]()
이것은 당신의 부서입니다.
원 방정식의 문제를 해결했습니다.
연습 1
중심이 점에 있는 반지름이 5인 원의 일반 방정식을 계산합니다.
![]()
원의 일반 방정식을 찾으려면 먼저 일반 방정식을 찾아야 합니다. 이를 위해 원의 일반 방정식에 대한 공식을 사용합니다.
![]()
![]()
![]()
일반 방정식을 알고 나면 원의 일반 방정식을 찾을 때까지 작업합니다.
![]()
![]()
![]()
![]()
따라서 원의 일반 방정식은 다음과 같습니다.
![]()
연습 2
다음 각 원에 대해 중심 좌표와 반지름의 길이를 구하세요.
![]()
![]()
![]()
둘레 A)
![]()
원주는 일반 방정식의 형태로 표현되며 그 공식은 다음과 같습니다.
![]()
따라서 원의 중심 좌표는 다음과 같습니다.
![]()
![]()
반경은 다음과 같습니다.
![]()
![]()
둘레 B)
![]()
이 원주는 일반 방정식의 형태로 표현되므로 중심 좌표를 계산하려면 다음 공식을 사용해야 합니다.
![]()
![]()
![]()
![]()
반면에 원의 반지름을 구하는 공식은 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b0cdc38937e6c36bb9e6d2ca0814a650_l3.png)
둘레 C)
![]()
원주는 일반 방정식의 형태로 표현되며 그 공식은 다음과 같습니다.
![]()
따라서 원의 중심 좌표는 다음과 같습니다.
![]()
이 경우 방정식에는 항이 없습니다.
![]()
어느 것도 아니다
![]()
따라서 좌표의 원점을 중심으로 합니다.
![]()
반경은 다음과 같습니다.
![]()
![]()
연습 3
다음 방정식 중 원의 방정식은 무엇입니까?
![]()
![]()
![]()
![]()
식이 원의 방정식이 되려면 다음 조건이 충족되어야 합니다.
1. 계수
![]()
그리고
![]()
1과 같아야 합니다.
2. 방정식에는 항이 있을 수 없습니다.
![]()
삼.
 따라서 우리는 각 방정식에 대해 세 가지 조건이 충족되는지 확인해야 합니다.
따라서 우리는 각 방정식에 대해 세 가지 조건이 충족되는지 확인해야 합니다.
방정식 A)
![]()
계수
![]()
그리고
![]()
은 1이고 방정식에는 항이 없습니다.
![]()
따라서 세 번째 조건을 확인하는 것으로 충분합니다.

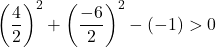
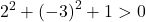
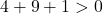
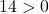 방정식은 3가지 조건을 만족하므로 원의 방정식이 됩니다.
방정식은 3가지 조건을 만족하므로 원의 방정식이 됩니다.
방정식 B)
![]()
방정식에는 다음과 같은 항이 있습니다.
![]()
방정식이 원에 해당하지 않는 경우.
방정식 C)
![]()
계수
![]()
그리고
![]()
는 1이 아니지만 모든 항을 나누어 방정식을 변환할 수 있습니다.
![]()
이런 식으로 이제 계수는
![]()
그리고
![]()
예, 그들은 1이고 게다가 방정식에는 항이 없습니다
![]()
따라서 우리는 세 번째 조건만 확증하면 됩니다.

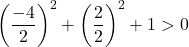
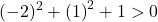
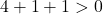
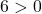 방정식은 3가지 조건을 만족하므로 원의 방정식이 됩니다.
방정식은 3가지 조건을 만족하므로 원의 방정식이 됩니다.
방정식 D)
![]()
계수
![]()
그리고
![]()
은 1이고 방정식에는 항이 없습니다.
![]()
따라서 세 번째 조건을 확인하는 것으로 충분합니다.

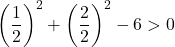
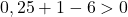
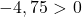 방정식은 마지막 조건을 만족하지 않으므로 원의 방정식이 아닙니다 .
방정식은 마지막 조건을 만족하지 않으므로 원의 방정식이 아닙니다 .
연습 4
다음 세 점을 통과하는 원의 방정식을 결정합니다.
![]()
모든 원의 일반 방정식은 다음과 같습니다.
![]()
따라서 매개변수를 찾기 위해서는 점의 좌표를 원 방정식에 대입해야 합니다.
![]()
![]()
그리고
![]()
첫 번째 점으로 우리는 계수를 찾습니다.
![]()
![]()
두 번째 점을 사용하여 계수를 찾습니다.
![]()
![Rendered by QuickLaTeX.com \begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-12719654d98ba81f0a7d45e587478e6d_l3.png)
그리고 세 번째 점에서 우리는 계수를 찾습니다.
![]()
![Rendered by QuickLaTeX.com \begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f1e69c28996a8fbfa14189c48a295095_l3.png)
결론적으로 원주에 대한 일반 방정식은 다음과 같습니다.
![]()
연습 5
원의 반대쪽 끝이 다음 두 점인 경우:
![]()
원의 일반 방정식은 무엇입니까?
두 점이 원의 극단인 경우 중심은 다음 두 점 사이의 중간점이 됩니다.
![]()
![]()
![]()
반면, 원의 지름은 두 점 사이의 거리이며, 이는 두 점이 형성하는 벡터의 크기를 사용하여 계산할 수 있습니다.
![]()
![]()
그리고 원의 반지름은 지름의 절반입니다.
![]()
따라서 원의 일반 방정식은 다음과 같습니다.
![]()
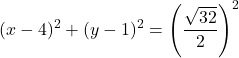
![]()
마지막으로, 이 기사가 도움이 되었다면 쌍곡선(수학) 및 포물선(수학) 페이지에도 관심이 있으실 것입니다. 쌍곡선과 포물선이 무엇인지, 방정식, 특성, 예, 풀이 연습 문제에 대한 자세한 설명을 찾을 수 있습니다.