벡터와 숫자의 곱셈

이 페이지에서는 숫자와 그래픽을 통해 벡터에 실수(또는 스칼라)를 곱하는 방법을 설명합니다. 또한 스칼라에 의한 벡터 곱의 예제와 해결 연습도 찾을 수 있습니다. 마지막으로 벡터를 사용한 이러한 유형의 연산 속성도 설명합니다.

벡터에 실수를 어떻게 곱하나요?

벡터와 숫자(또는 스칼라)의 곱을 수치적으로 계산하려면 벡터의 각 구성요소에 숫자를 곱해야 합니다.

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

$k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y)$

따라서 벡터에 숫자를 곱한 결과는 다음과 같은 특성을 가진 새로운 벡터를 생성합니다.

벡터와 스칼라를 곱하면 원래 벡터와 방향이 같은 새 벡터가 생성됩니다.
또한 숫자가 양수이면 새 벡터는 동일한 방향을 갖습니다.
또는 숫자가 음수이면 반대 의미를 갖습니다.
결과 벡터의 크기는 원래 벡터의 크기에 스칼라를 곱한 것과 동일합니다.

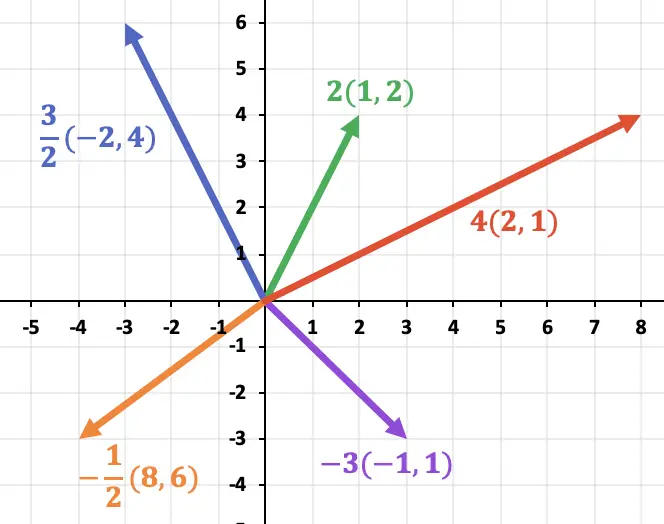
다음 그래프에서는 스칼라의 부호에 관계없이 벡터의 방향이 어떻게 유지되는지 확인할 수 있습니다. 반면 벡터의 방향은 곱하는 숫자의 부호에 따라 달라집니다.

또한 다음 그래프에서는 결과 곱 벡터의 크기가 원래 벡터의 크기에 스칼라를 곱한 것과 동일하다는 것을 분명히 알 수 있습니다.

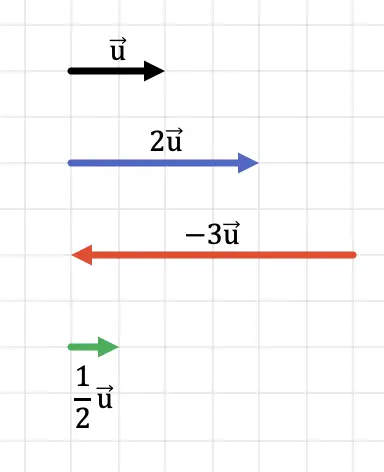
분명히, 벡터에 1보다 큰 숫자를 곱하면 결과는 더 긴 길이(더 큰 모듈러스)의 벡터가 됩니다. 반면, 벡터에 1보다 작은 숫자를 곱하면 결과는 더 짧은 길이(더 작은 모듈러스)의 벡터가 됩니다.

참고: 벡터와 스칼라의 곱을 벡터의 내적 과 혼동하지 마십시오. 이름은 비슷하지만 전혀 다른 개념입니다.

스칼라에 의한 벡터 곱의 예

다음으로 벡터와 숫자의 곱이 계산되는 방법에 대한 수치적 예를 살펴보겠습니다.

다음 벡터에 4를 곱합니다.

$\vv{\text{u}} =(2,-3)$

$4\cdot \vv{\text{u}} =(4 \cdot 2 \ , \ 4 \cdot (-3)) = \bm{(8,-12)}$

보시다시피, 이러한 유형의 벡터 연산은 많은 계산을 수행할 필요가 없기 때문에 그리 복잡하지 않습니다.

그러나 벡터 추가 및 벡터 빼기와 같은 더 복잡한 벡터 연산이 있습니다. 벡터와 스칼라의 곱을 계산하는 방법을 이미 이해했다면 다음 단계로 넘어가 벡터 덧셈 과 벡터 뺄셈을 해결하는 방법을 살펴보는 것이 좋습니다. 이는 다소 어려운 작업이며 실제로는 훨씬 더 많이 사용됩니다(더 중요합니다).

벡터에 숫자를 곱하는 속성

벡터와 숫자의 곱은 다음과 같은 속성을 갖습니다.

연관 속성 : 벡터에 둘 이상의 숫자를 곱할 때 곱셈의 순서는 중요하지 않습니다.

$k \cdot (k' \cdot \vv{\text{u}}) =(k\cdot k') \cdot \vv{\text{u}}$

벡터의 덧셈과 뺄셈에 관한 분배법칙 :

$k \cdot (\vv{\text{u}}+ \vv{\text{v}})=k\cdot \vv{\text{u}} + k\cdot \vv{\text{v}}$

$k \cdot (\vv{\text{u}}- \vv{\text{v}})=k\cdot \vv{\text{u}} - k\cdot \vv{\text{v}}$

스칼라 덧셈에 관한 분배법칙 :

$(k+k') \cdot \vv{\text{u}} =k\cdot \vv{\text{u}} + k'\cdot \vv{\text{u}}$

중립 요소 : 분명히 모든 벡터에 1을 곱하면 벡터 자체가 됩니다.

$1\cdot \vv{\text{u}} = \vv{\text{u}}$

스칼라에 의한 벡터의 곱셈 문제 해결

연습 1

다음 벡터의 곱 결과를 3으로 분석적으로 계산합니다.

$\vv{a}=(-2,5)$

해결책 보기

제품을 찾으려면 벡터의 각 좌표에 3을 곱해야 합니다.

$3\cdot \vv{a}=(3\cdot (-2), 3 \cdot 5) = \bm{(-6,15)}$

연습 2

다음 벡터에 6을 곱하고 해당 모듈을 찾습니다.

$\vv{a}=(3,-4)$

해결책 보기

먼저 벡터에 스칼라를 곱합니다.

$6\cdot \vv{a}=(6\cdot 3, 6 \cdot (-4)) = (18,-24)$

이제 얻은 벡터의 크기를 계산하는 두 가지 방법이 있습니다. 첫 번째는 원래 벡터의 크기를 구한 다음 여기에 6을 곱하는 것입니다.

$\lvert \vv{a} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{25} =5$

$6\cdot \lvert \vv{a} \rvert =6\cdot 5 =\bm{30}$

두 번째 방법은 곱셈에서 얻은 벡터의 크기를 직접 계산하는 것입니다.

$\lvert 6\cdot \vv{a} \rvert =\sqrt{18^2+(-24)^2} = \sqrt{900} =\bm{30}$

따라서 두 절차 모두 결과가 모듈러스를 계산하는 방법에 의존하지 않는 것으로 나타났습니다.

연습 3

다음 벡터에서:

$\vv{a}=(4,-1)$

다음 연산을 대수적으로 계산합니다.

$2\cdot \vv{a}$

$-3\cdot \vv{a}$

$\displaystyle \frac{1}{2} \cdot \vv{a}$

$4\cdot \vv{a}$

다음으로, 결과 벡터가 원래 벡터와 동일한 방향 및 방향을 가지고 있는지 확인하고 가장 짧은 것부터 가장 긴 것 순으로 정렬합니다.

해결책 보기

먼저 곱셈을 계산합니다.

$2\cdot \vv{a}=(2\cdot 4, 2 \cdot (-1)) = (8,-2)$

$-3\cdot \vv{a}=(-3\cdot 4, -3 \cdot (-1)) = (-12,3)$

$\displaystyle \frac{1}{2}\cdot \vv{a}=\left(\frac{1}{2}\cdot 4, \frac{1}{2} \cdot (-1)\right) = \left(2,-\frac{1}{2}\right)$

$4\cdot \vv{a}=(4\cdot 4, 4 \cdot (-1)) = (16,-4)$

따라서 양수를 곱한 벡터는 원래 벡터와 방향 및 방향이 동일합니다. 그리고 음수를 곱한 벡터는 원래 벡터와 방향은 같지만 방향이 반대입니다.

같은 방향과 같은 방향의 벡터:

$\displaystyle 2\vv{a}, \ 4\vv{a}$

그리고

$\displaystyle \frac{1}{2}\vv{a}$

방향은 같지만 의미가 다른 벡터:

$-3\vv{a}$

마지막으로 벡터의 길이 또는 동등한 모듈에 따라 벡터의 순서를 지정해야 합니다. 가장 긴 길이의 벡터(또는 가장 큰 모듈)는 더 큰 숫자(절대값)를 곱한 벡터가 되고, 가장 짧은 길이의 벡터(또는 가장 작은 모듈)는 더 작은 숫자를 곱한 벡터가 됩니다. 숫자(절대값). 따라서 길이 순서는 다음과 같습니다.

$\displaystyle \begin{vmatrix} \displaystyle\frac{1}{2}\vv{a}\end{vmatrix} <\lvert 2\vv{a}\rvert < \lvert -3\vv{a}\rvert < \lvert 4\vv{a}\rvert$