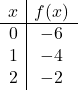이 페이지에서는 절대값 함수가 무엇인지 설명합니다. 또한 조각별 절대값 함수를 정의하는 방법과 이러한 유형의 함수를 그래프에 나타내는 방법도 배웁니다. 또한, 절대값 함수의 예시를 함께 볼 수 있으며, 단계별로 연습문제와 해결문제를 통해 연습할 수 있습니다.
절대값 함수란 무엇입니까?
절대값 함수의 정의는 다음과 같습니다.
함수의 절대값은 모든 이미지를 긍정적인 이미지로 변환합니다. 따라서 절대 함수의 경로는 음수 값을 가질 수 없습니다.
다음 함수는 절대값 함수의 예입니다.
![]()
특정 지점에서 함수를 평가할 때 긍정적인 결과를 얻으면 긍정적인 상태로 유지됩니다.
![]()
반면에 결과가 부정적이면 긍정적이 됩니다.
![]()
절대값 함수는 일반적으로 고등학교에서 제공됩니다. 그 이유는 그 특성으로 인해 이해하기가 약간 어렵기 때문입니다.
절대값을 갖는 함수를 조각별로 정의하는 방법
절대값 함수는 조각별 함수로 표현될 수 있습니다. 이렇게 하려면 음수 구간에서 함수의 부호를 변경해야 합니다.
절대값 함수에서 조각별 함수로 이동하는 방법의 예를 살펴보겠습니다.
- 다음 함수를 절댓값으로 조각별 함수로 표현합니다.
![]()
우리가 가장 먼저 해야 할 일은 함수가 음수일 때를 결정하는 것입니다. 이를 위해 절대값을 0으로 설정하고 방정식을 푼다.
![]()
![]()
![]()
![]()
![]()
이제 라인에서 얻은 값을 나타냅니다.
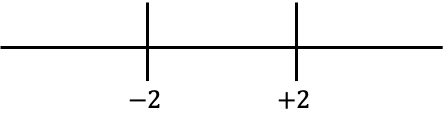
그리고 선의 각 간격에서 절대값이 없는 함수를 갖는 부호가 무엇인지 살펴봅니다.
![]()
예를 들어 -2보다 작은 점을 취합니다.
![]()
![]()
![]()
부정적인
![]()
예를 들어 -2와 +2 사이의 임의의 점을 취합니다.
![]()
![]()
![]()
긍정적인
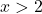
![]()
![]()
![]()
부정적인

우리가 본 것처럼 절대값이 없는 함수는 구간에서 음수가 됩니다.
![]()
그리고

![\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -(4-x^2) & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -(4-x^2) & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”372″ style=”vertical-align: 0px;”></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5f441ea5792fb5cc7ba8300f71defef_l3.png)
![\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x<-2 \\[2ex] 4-x^2 & \text{si} & -2 \le x \le 2 \\[2ex] -4+x^2 & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”358″ style=”vertical-align: 0px;”></p>
</p>
<p> 일부 간격에서는 동등성을 포함해야 합니다. 예를 들어 여기서는 두 번째 간격에 넣습니다.</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-89ab8a514afe36c94d7072efe47ef507_l3.png)
![]()
. 그러나 모든 중요한 지점이 동점인 한 원하는 간격으로 배치할 수 있습니다. 즉, 다음과 같이 함수를 정의해도 마찬가지입니다.
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-5cce3bcc22edb3a7f511cea0a1c32372_l3.png)
절대값으로 함수를 표현하는 방법
그래프에 절대값을 갖는 함수를 나타내려면 아래 설명된 단계를 따라야 합니다.
- 절대값이 없는 것처럼 함수를 표현합니다.
- 함수가 음수인 구간, 즉 X축 아래에 있는 구간에 대칭함수를 그려주세요.
- X축 아래에 있는 함수 부분을 삭제합니다.
절대값을 사용하여 함수를 그래프로 표시하는 방법의 예를 살펴보겠습니다.
- 다음 함수를 절대값으로 그래프로 나타내세요.
![]()
절대값이 있는 함수를 표현하려면 먼저 절대값이 없는 함수를 표현해야 합니다. 따라서 절대값 없이 함수 값 테이블을 만듭니다.
![]()
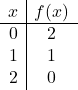
점을 그래프로 표시하고 마치 일반 함수인 것처럼 선을 그립니다.
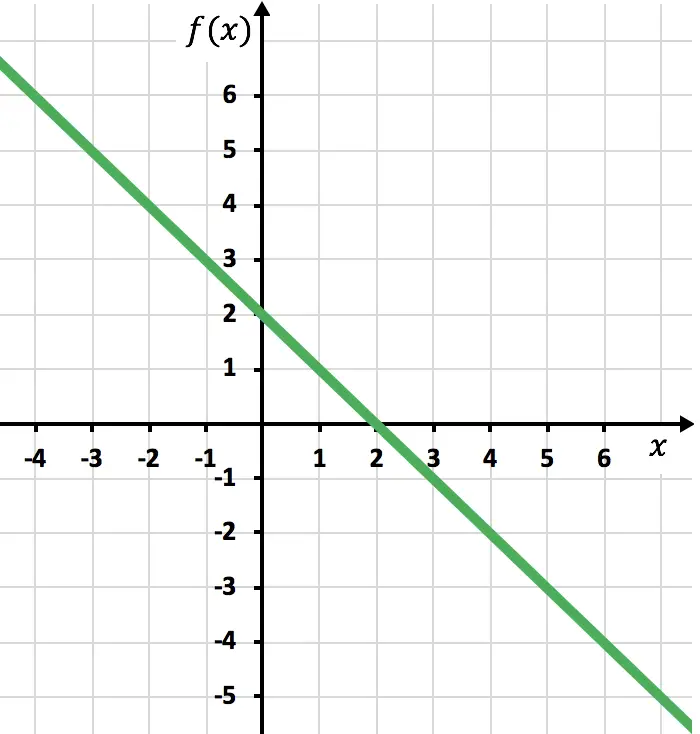
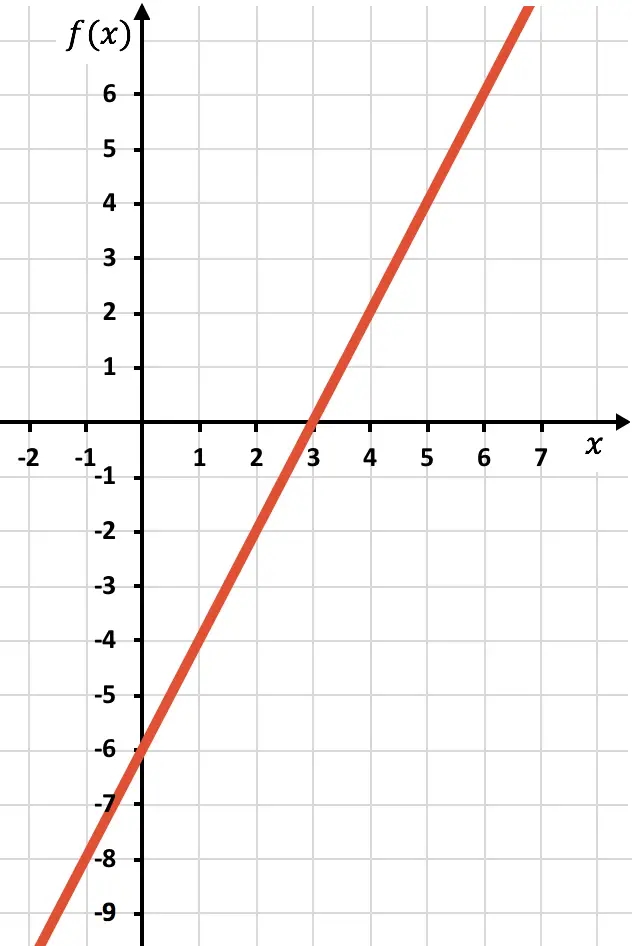
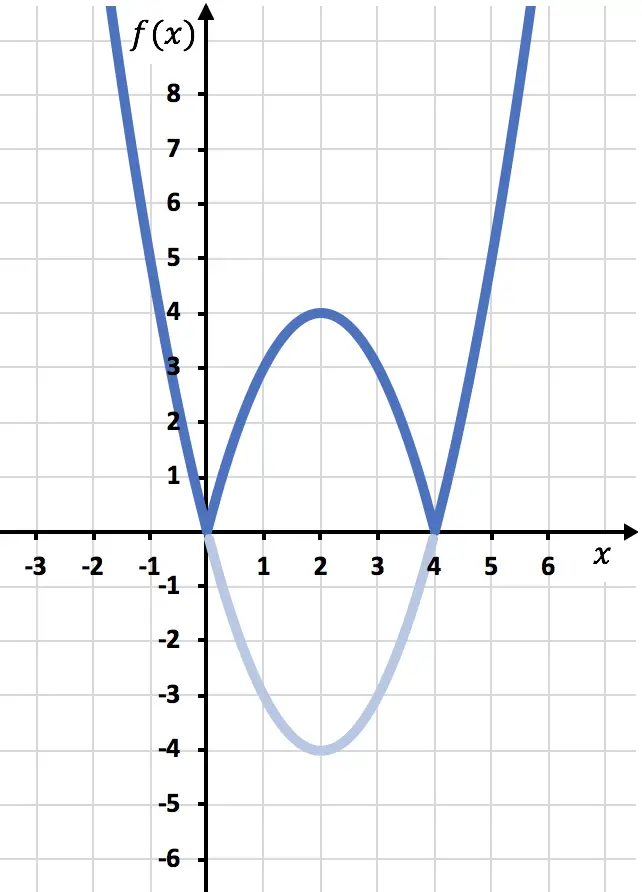
이제 함수가 음수인 대칭 함수, 즉 x축 아래에 있는 대칭 함수를 그려야 합니다. 따라서 x=2부터 시작하여 함수를 반대로 바꿉니다.
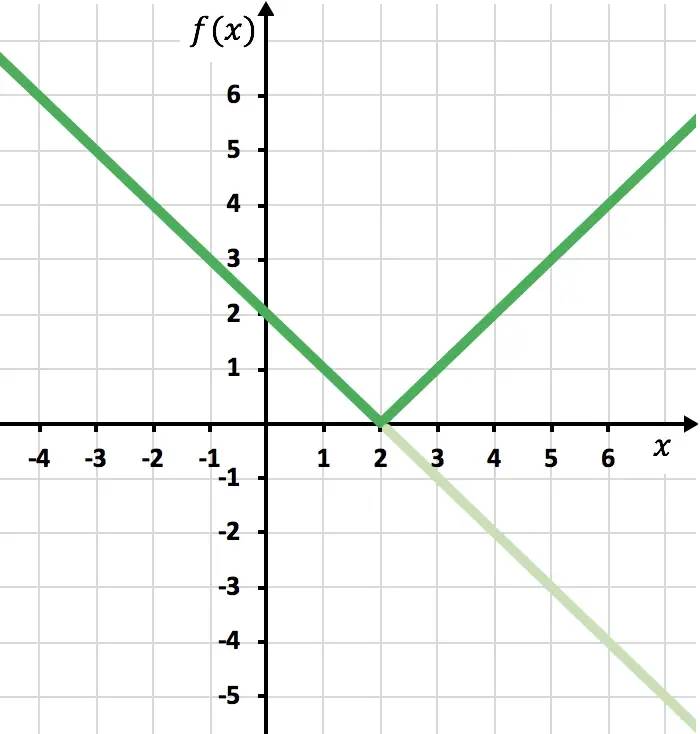
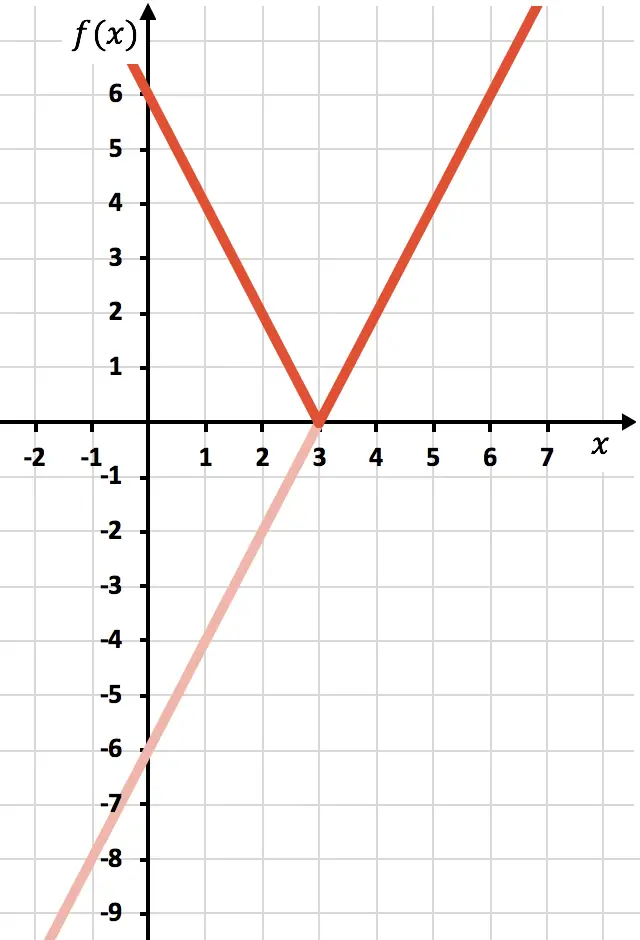
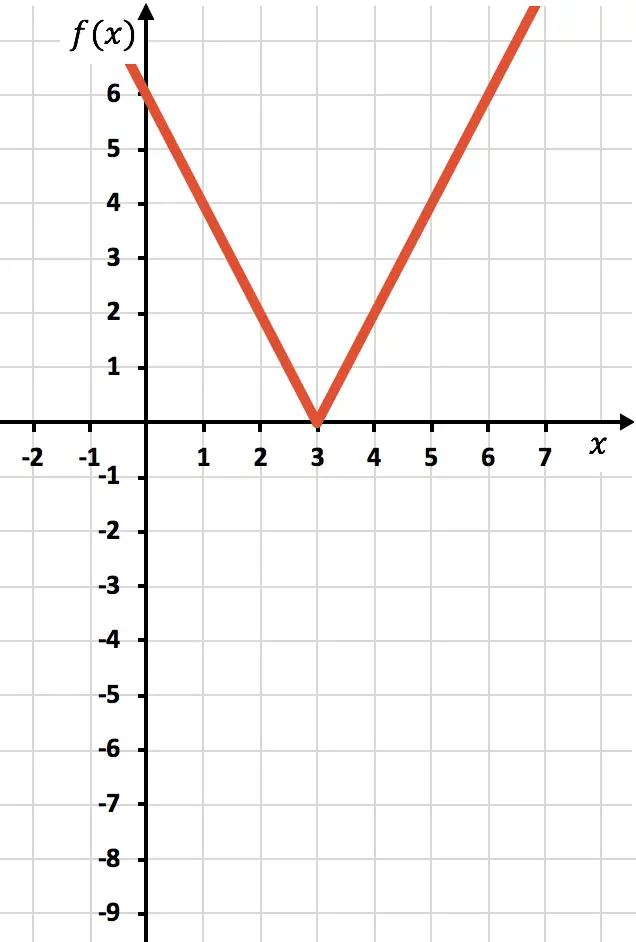
마지막으로 X축 아래에 있는 함수의 흔적을 제거합니다.

그리고 이런 방식으로 우리는 이미 함수를 절대값으로 표현했습니다. 보시다시피, 유일하게 변경되는 점은 OX 축 아래에 있는 함수 부분을 반전시켜야 한다는 것입니다. 따라서 절대값을 갖는 모든 함수의 그래프는 항상 양의 반 Y축 쪽에 놓이게 됩니다.
한편, 개념을 검토해 보면, 그래프를 통해 이전 절대값 함수의 영역이 전적으로 실수로 구성되어 있음을 추론할 수 있습니다. 반면, 절대값을 갖는 상기 함수의 범위 또는 범위는 양수와 0만으로 구성된다.
절대값 함수에 대한 연습문제 해결
연습 1
다음 함수를 절댓값으로 조각별 함수로 표현합니다.
![]()
먼저 함수가 음수일 때를 살펴봐야 합니다. 이를 위해 절대값을 0으로 설정하고 방정식을 풉니다.
![]()
![]()
우리는 라인에서 찾은 값을 나타냅니다.
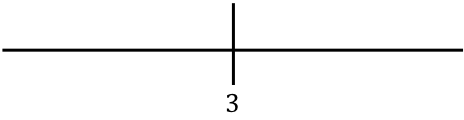
이제 절대값 없이 함수의 각 간격에서 점을 평가하여 함수가 선의 각 섹션에 실제로 어떤 부호를 가지고 있는지 알아냅니다.
![]()
예를 들어, 3보다 작은 점을 취합니다.
![]()
![]()
![]()
긍정적인
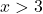 예를 들어, 3보다 큰 점을 취합니다.
예를 들어, 3보다 큰 점을 취합니다.
![]()
![]()
![]()
부정적인
절대값이 없는 함수는 x>3 구간에서 음수가 됩니다. 따라서 우리는 이 간격에서 부호를 변경하여 함수를 대시로 표현해야 합니다.
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-f7cfaaff9890b356f1db6805ed94dbb8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d249715b500ad03c44ab6ab5838e32e8_l3.png)
연습 2
절대값을 사용하여 다음 함수의 조각별 표현을 찾습니다.
![]()
우리가 가장 먼저 해야 할 일은 함수가 음수일 때를 결정하는 것입니다. 이렇게 하려면 절대값 인수를 0으로 설정하고 방정식을 풀어야 합니다.
![]()
![]()
![]()
![]()
![]()
이제 오른쪽에서 얻은 함수의 근을 나타냅니다.
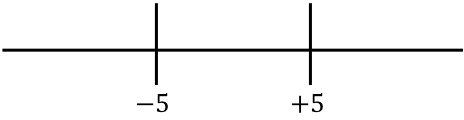
그리고 선의 각 간격에서 절대값이 없는 함수를 갖는 부호가 무엇인지 살펴봅니다.
![]()
예를 들어 -5보다 작은 점을 취합니다.
![]()
![]()
![]()
![]()
긍정적인
![]()
예를 들어 -5에서 +5 사이의 임의의 지점을 취합니다.
![]()
![]()
![]()
![]()
부정적인
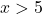 예를 들어 5보다 큰 점을 취합니다.
예를 들어 5보다 큰 점을 취합니다.
![]()
![]()
![]()
![]()
긍정적인

따라서 절대값이 없는 함수는 -5<x<5 구간에서만 음수가 됩니다. 따라서 이 구간의 부호만 변경하여 함수를 부분적으로 표현해야 합니다.
![\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”408″ style=”vertical-align: 0px;”></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e0fad2e3a9e1a6d1edcde507e60230b_l3.png)
![\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -3x^2+75 & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”394″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-5f9638fe87ad09d7dbcdb8e30a16688f_l3.png)