단항식은 변수에 지수를 곱한 계수(수치)로 구성된 대수식 입니다. 예를 들어 4x²라는 표현식은 단항식입니다. 그래서 이 수학적 개념으로부터 우리는 여러 단항식의 덧셈과 뺄셈의 집합인 다항식에 도달합니다. 위 이미지에서 여러 단항식으로 구성된 다항식 구조의 예를 볼 수 있습니다.
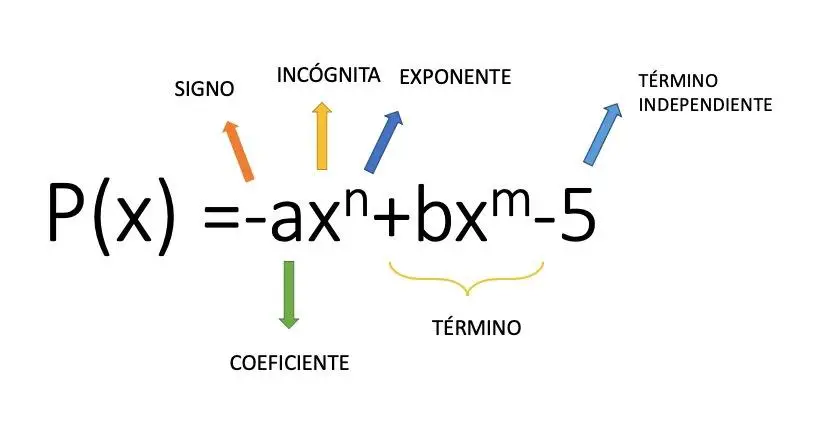
다항식의 종류
특정 단항식의 지수를 통해 다항식을 여러 유형으로 분류할 수 있습니다. 이러한 표현식을 1차 다항식, 2차 다항식, 3차 다항식 등과 같은 범주로 분류할 수 있습니다. 기본적으로 가장 큰 지수를 갖고 다항식의 차수가 되는 단항식을 식별해야 합니다. 그리고 일단 알고 나면 방금 이야기한 유형 중 하나로 분류할 수 있습니다.
여러 변수의 다항식
또한 다항식을 구성하는 단항식의 수에 따라 다항식을 구성하는 또 다른 방법도 있습니다. 예를 들어, 이항식이 있는 경우 이는 두 개의 항을 갖는 다항식을 갖는 것과 동일하며, 삼항식을 갖는 경우 이는 세 개의 항을 갖는 다항식을 갖는 것과 동일합니다. 다항식을 분류하는 이러한 모든 방법에는 무한히 많은 하위 범주가 있습니다. 이러한 표현식은 우리가 원하는 어떤 단항식으로도 구성될 수 있고 어떤 차수도 가질 수 있습니다.
다항식의 특성과 속성
- 다항식의 절대 차수: 이전 섹션에서 상대 차수의 정의에 대해 논의했습니다. 그러나 하나 이상의 변수로 구성된 다항식의 경우, 이 단항식의 모든 변수 지수의 최대 합과 동일한 절대 차수를 갖습니다. 예를 들어, 단항식 5x²y³에서 절대 차수는 2 + 3 = 5와 같습니다.
- 순서 다항식: 변수의 지수가 오름차순 또는 내림차순으로 배열된 변수에 대해 순서 다항식을 정의합니다. 예를 들어, 이 다항식 P(x) = 3x + 4x³ – x²를 찾으면 이 경우에는 순서가 지정되지 않습니다. 따라서 이를 수정해야 하며 다음 결과를 얻습니다. P(x) = 4x³ – x² + 3x.
- 완전 다항식: 가능한 모든 지수(최고 차수부터 독립항까지)를 갖는 단항식을 갖는 다항식을 찾을 때, 우리는 그것이 완전 다항식 이라고 말합니다. 예를 들어, 다음 표현식: P(x) = 3 x² + 2x – 4는 2와 0 사이에 누락된 지수가 없기 때문에 이 유형입니다.
- 동차 다항식: 각 단항식의 절대차수가 동일한 다항식입니다. 변수는 지수에서 서로 다른 값을 가질 수 있지만, 모든 단항식에서 변수의 지수의 합은 반드시 동일해야 합니다. 예: P(x) = x²y³z + 3 x 4 yz, 두 합은 6개의 2 + 3 + 1 = 4 + 1 + 1 = 6을 제공합니다.
- 동일한 다항식: 동일한 항의 계수를 공유하는 두 개 이상의 다항식을 찾으면 해당 다항식을 동일한 다항식이라고 말합니다. 아래에서 두 다항식 사이의 예를 볼 수 있습니다: P(x) = 2x + 27 및 Q(x) = 5 (x + 3) – 3 (x – 4), 그들은 각 지수의 계수를 공유하기 때문에 동일합니다. : 2x = 5x – 3x 및 27 = 15 + 12.
- 영 다항식: 이 다항식에는 계수가 0(0과 같음)만 있으므로 다항식의 전체 값도 0이 됩니다. 다항식 P(x) = 0x³ + 0x² – 0x – 0은 이러한 유형의 다항식의 명확한 예이지만 Q(x) = 0과 혼동해서는 안 됩니다. 왜냐하면 이 경우 방정식을 형성하지만 방정식이 성립하지 않기 때문입니다. 이는 Q(x)의 모든 계수가 0이라는 의미는 아닙니다.
다항식의 수치
다항식의 수치는 이 표현식의 변수를 숫자로 대체하여 얻을 수 있는 결과입니다. 우리는 마치 결합된 연산 인 것처럼 이 다항식을 풀기만 하면 됩니다. 다음으로, 이와 같은 표현식의 수치를 얻는 데 사용할 수 있는 세 가지 방법을 설명하겠습니다.
- 직접 대체: 다항식의 각 변수에 해당하는 값이 직접 주어지면 이러한 변수를 해당 숫자로 대체하면 됩니다. 이런 식으로 다항식 P(x) = 2x² – x + 4가 있고 x = 3이라고 말하면 다항식의 수치 값은 2 · 3² – 3 + 4 = 19와 같습니다.
- 변수 해결: 변수의 값을 직접 제공하지 않지만 동등성을 제공하는 경우 이 사례를 적용합니다. 예를 들어 P(x – 1) = x³ – 2x + 1이 참인 경우 P(2)는 먼저 방정식 2 = x – 1을 풀고 x = 3을 얻습니다. 마지막으로 3을 다음으로 대체해야 합니다. x, 3³ – 2 · 3 + 1 = 22가 됩니다.
- 변수 변경: 다항식 P(x) = 4x – 2가 있고 P(x + 2)에 대한 이 값을 알고 싶을 때. 다음으로 표현식의 모든 x를 a(x+2)로 변경해야 합니다. 즉, 마지막으로 해결된 예가 P(x + 2) = 4(x + 2) – 2처럼 보이는지 살펴보겠습니다.
다항식을 사용한 연산
아래에서는 항상 연산 계층을 따라 다항식을 사용하여 네 가지 기본 산술 연산을 해결하는 방법을 설명합니다. 각 섹션에서는 각 사례에서 진행하는 방법을 알 수 있는 작은 이론과 몇 가지 실제 사례를 찾을 수 있습니다.
다항식의 추가
다항식을 추가하려면 유사한 용어 로만 그룹화할 수 있다는 사실을 고려해야 합니다. 따라서 다항식 P(x) = 3x³ – x² + 2x – 4 및 Q(x) = 2x² + 3x – 2가 있는 경우. 따라서 P(x) + Q(x)를 만들기 위해 동일한 지수를 수반하는 두 다항식의 계수를 추가합니다. P(x) + Q(x) = 3x³ + (-x) ² + 2x²) + ( 2x + 3x) + (-4 -2) = 3x³ + x² + 5x – 6. 요약하면 유사한 각 항의 계수를 그룹화하고 추가했으며 결국 모든 항을 단일 다항식으로 표현했다고 말할 수 있습니다. .
다항식의 뺄셈
다항식의 뺄셈은 덧셈과 같은 방식으로 해결됩니다. 유일한 차이점은 분명히 기호입니다. 그런 다음 비슷한 용어를 그룹화하고 빼서 하나의 표현으로 변환합니다. 아래에서는 예를 사용하여 보여줍니다. P(x) = 5x³ – 2x² + x – 3 및 Q(x) = 3x² + 5x + 4, 그런 다음 P(x) – Q(x ) = 5x³ + (-2x² + 3x²) + (x + 5x) + (-3 + 4) = 5x³ + x² + 6x + 1.
다항식 곱셈
이러한 유형의 곱셈을 풀 때 상황이 약간 복잡해질 수 있지만, 우리가 알려드리는 모든 단계를 따르면 괜찮을 것입니다. 이 수학적 연산에서 모든 단항식은 다른 단항식과 함께 작동합니다. 이는 유사한 항만 곱하는 것이 아니라는 것을 의미합니다. 또한 계수만 변경되는 것이 아니라 지수도 변경됩니다 . 이 예를 사용하면 모든 것을 훨씬 더 잘 이해할 수 있습니다: P(x) = 2x² + 3x – 1 및 Q(x) = 2x + 3:
피(엑스) Q(엑스) = ( 2x² + 3배 –1 ) · ( 2배 + 삼 ) = 2x² · 2배 + 2x² · 삼 + 3배 · 2배 + 3배 · 삼 + (-1 ) · 2배 + (-1 ) · 삼 = 4x³ + 6x² + 6x² + 9x – 2x – 3 = 4x³ + 12x² + 7x – 3
기본적으로 다항식의 각 항의 계수에 두 번째 항의 계수를 모두 곱한 다음 n · a m = a n+m 의 거듭제곱 속성을 적용합니다.
다항식의 나눗셈
마지막으로, 다항식의 나눗셈을 푸는 방법만 설명하면 됩니다. 기본적으로 나눗셈의 분배 법칙을 적용해야 합니다: (a + b + c) ¼ d = (a ¼ d) + (b ¼ d) + (c ¼ d). 그리고 n ¼ a m = a nm 에도 다음과 같은 지수법칙을 적용하겠습니다. 이제 간단한 예를 통해 이를 살펴보겠습니다: P(x) = 3x³ – 6x² + 9x 및 Q(x) = 3x.
P(x) ¼ Q(x) = ( 3x³ – 6x² +9배 ) ¼ 3배 = ( 3x³ ¶ 3배 ) + ( 6x² ¶ 3배 ) + (9배 ¶ 3배 ) = x² – 2x + 3
이제 다항식을 사용하여 이러한 모든 연산을 해결하는 방법을 살펴보았으므로 이를 실제로 적용하는 방법을 알기를 바랍니다. 그러나 이것이 사실이 아니라고 생각하고 계속해서 조금 연습하고 싶다면 이 페이지에서 해결된 몇 가지 연습 문제를 살펴보는 것이 좋습니다. 이는 이러한 모든 수학적 개념을 내면화하는 데 도움이 될 것입니다.
다항식 인수분해
다항식을 인수분해 하려면 이 마지막 링크의 기사에 설명된 대로 수동으로 수행하거나 Ruffini 계산기를 사용하여 수행할 수 있습니다. 빨리 하고 싶다면 이 두 번째 옵션을 사용하는 것이 좋습니다. 하지만 단지 인수분해 방법을 배우는 중이라면 수동으로 연습하는 것이 더 좋습니다. 이를 수행하는 방법은 상황에 따라 선택해야 합니다.
공학용 계산기로 다항식 풀기
오늘날 시장에는 다양한 공학용 계산기가 있습니다. 하지만 다항식을 풀 수 있는 저렴한 계산기를 찾고 있다면 Casio FX-991SPX II를 추천합니다. 사용하기 쉽고 매우 강력하며 기능적이어서 중학교 및 고등학교 수학 학생에게 적합합니다. 아래에서는 이 모델이나 유사한 Casio 모델을 사용하여 이 스타일의 수학적 표현을 어떻게 해결하는지 간략하게 설명합니다.
먼저 변수의 숫자 값을 입력하고 이를 쓴 다음 “STO” + 변수 문자 (예: x)를 눌러야 합니다. 따라서 모든 변수가 정의되면 모든 변수와 모든 숫자를 그대로 다항식으로 작성하면 됩니다. 마지막으로 등호 키를 눌러야 합니다. 이렇게 하면 다항식의 수치와 동일한 결과를 얻을 수 있습니다.