이 페이지에서는 이차 함수가 무엇인지와 그 모든 특성(곡률, 꼭지점, 축과의 교차점 등)에 대해 설명합니다. 또한 그래프에서 이차 함수를 표현하는 방법도 배웁니다. 마지막으로 이차 함수에 대한 예제, 단계별 연습 및 문제를 통해 연습할 수 있습니다.
이차 함수란 무엇입니까?
이차 함수의 정의는 다음과 같습니다.
수학에서 2차(또는 포물선) 함수는 2차 다항식 함수, 즉 최고 차수가 2차인 함수입니다. 따라서 이차 함수의 공식은 다음과 같습니다.
![]()
금:
-
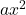
는 이차항입니다.
-
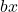
선형 용어입니다.
-

독립된 용어이다.
이차 함수의 정의역은 항상 실수로 구성됩니다.
![]()
이차 함수의 오목함과 볼록함
2차 함수 또는 포물선 함수의 곡률을 분석하는 것은 2차 계수에만 의존하기 때문에 매우 간단합니다.
- 계수

양수이면 이차 함수는 볼록합니다 (형식:

). 따라서 정상 회담은 최소한입니다.
- 계수

음수이면 이차 함수는 오목합니다 (모양은 다음과 같습니다).

). 따라서 피크는 최대입니다.


참고: 수학계에서는 여전히 완전히 동의하지 않기 때문에 일부 교수들은 그 반대라고 말합니다. 그들은 함수를 오목 함수라고 부릅니다.
![]()
, 그리고 다음과 같은 형태의 볼록 함수
![]()
. 어쨌든 중요한 것은 이름이 무엇이든 어떤 형태로 기능을 갖고 있는가이다.
이차 함수의 꼭지점
이차함수를 그래프로 나타내기 위해서는 포물선의 꼭짓점의 좌표를 알아야 합니다.
이차 함수의 꼭지점을 찾으려면 다음 공식을 사용하여 점의 X 좌표를 계산해야 합니다.
![]()
그런 다음 해당 지점에서 함수의 이미지를 계산하여 다른 정점 좌표를 찾을 수 있습니다.
![]()
따라서 이차 함수(또는 포물선)의 정점 좌표는 다음과 같습니다.
![]()
이차 함수의 축을 사용한 절단점
포물선은 항상 y축(Y축)과 교차하며, 이는 다음과 같은 경우에 발생합니다.
![]()
따라서 Y축을 사용하여 이차 함수의 컷오프 지점을 계산하려면 다음을 풀어야 합니다.
![]()
예를 들어, 다음 이차 함수의 OY 축과의 교차점은 다음과 같습니다.
![]()
![]()
![]()
한편, x축(X축)을 갖는 이차함수의 컷오프 포인트는 다음과 같은 경우에 발생한다.
![]()
따라서 X축과의 교차점을 계산하려면 다음 방정식을 풀어야 합니다.
![]()
예를 들어, 아래는 동일한 이차 함수의 OX 축을 사용하여 컷오프 지점을 계산한 것입니다.
![]()
![]()
우리는 일반 공식을 사용하여 이차 방정식을 푼다.
![]()
![]()
따라서 X축과 2차 함수의 교차점은 다음과 같습니다.
![]()
이 경우, 우리는 이차 방정식에 대해 단 하나의 해를 얻었지만 두 개의 해를 얻을 수도 있었습니다. 이 경우 이는 2차 함수가 서로 다른 두 지점에서 X축과 교차함을 의미합니다.
2차 또는 포물선 함수 표현의 예
예제를 사용하여 그래프에서 2차 함수를 표현하는 방법을 살펴보겠습니다.
- 다음 함수를 그래프로 나타내십시오.
![]()
가장 먼저 할 일은 포물선의 꼭지점을 계산하는 것입니다. 이를 위해 위에서 본 공식을 사용합니다.
![]()
정점이 어디에 있는지 알고 나면 값 테이블을 구성해야 합니다. 꼭지점과 그 주변 점에서 함수의 값을 계산합니다.
![]()
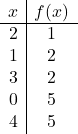
포물선을 더 잘 그리기 위해 데카르트 축을 사용하여 2차 함수의 절단점을 계산할 수도 있지만 이것이 반드시 필요한 것은 아닙니다.
이제 그래프에서 얻은 점을 나타냅니다 .
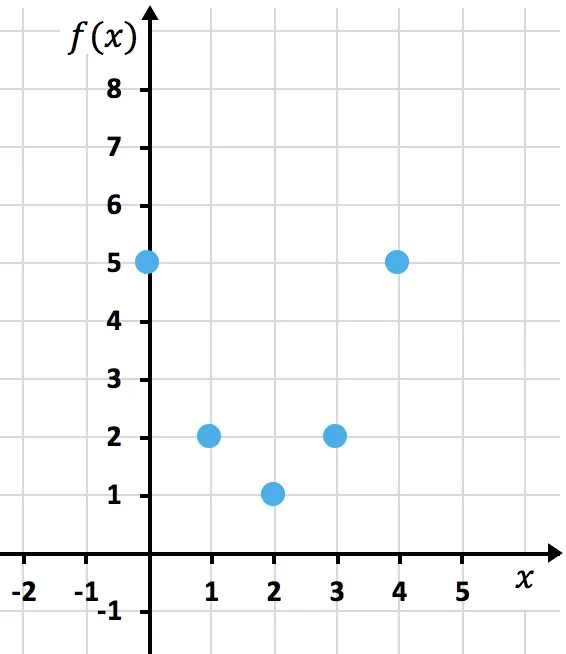
그리고 마지막으로 포물선을 이루는 점들을 연결합니다. 그런 다음 포물선의 가지를 늘려 위쪽으로 계속된다는 것을 나타냅니다.

이차 함수에 대한 해결 연습
연습 1
다음 이차 함수의 꼭지점을 찾으세요.
![]()
먼저 다음 공식을 사용하여 정점의 X 좌표를 계산합니다.
![]()
이제 해당 지점에서 함수를 평가하여 다른 좌표를 계산합니다.
![Rendered by QuickLaTeX.com \begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6067325564a5af06f7384d76157f3aa_l3.png)
따라서 이차 함수의 꼭지점은 다음과 같습니다.
![]()
연습 2
축을 사용하여 다음 함수의 컷오프 지점을 찾습니다.
![]()
Y축으로 절단점을 계산하려면 다음을 계산해야 합니다.
![]()
![]()
따라서 함수는 다음 지점에서 Y축을 통과합니다.
![]()
그리고 X축으로 절단점을 찾으려면 풀어야 할 문제가 있습니다.
![]()
![]()
![]()
우리는 다음 공식을 사용하여 이차 방정식의 근을 계산합니다.
![]()
![Rendered by QuickLaTeX.com \displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d909ba6581faf5916f0b1c0df7e471f_l3.png)
따라서 이 함수는 X축을 두 지점에서 자릅니다.
![]()
연습 3
다음 이차 함수를 그래프로 나타내십시오.
![]()
이것은 이차 함수입니다. 결과적으로 이를 표현하려면 먼저 다음 공식을 사용하여 포물선 꼭지점의 가로좌표를 계산해야 합니다.
![]()
이제 값 테이블을 만듭니다. 이를 위해 우리는 다음의 값을 계산합니다.
![]()
상단 및 상단 주변:
![]()
![]()
![]()
![]()
![]()
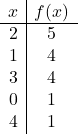
마지막으로 그래프에 점을 표시하고 포물선을 그립니다.

연습 4
다음 이차 함수를 그래프로 나타내십시오.
![]()
이는 2차 함수입니다. 결과적으로 이를 표현하려면 먼저 다음 공식을 사용하여 포물선 정점의 가로좌표를 찾아야 합니다.
![]()
이제 우리는 가치표를 작성합니다. 이를 위해 우리는 다음의 값을 계산합니다.
![]()
상단 및 상단 주변:
![]()
![]()
![]()
![]()
![]()

마지막으로 그래프에 점을 표시하고 포물선을 그립니다.

연습 5
그래프에 다음과 같은 불완전 이차 함수를 플롯합니다.
![]()
이는 2차 다항식 함수입니다. 결과적으로 이를 표현하려면 먼저 다음 공식을 사용하여 포물선 꼭지점의 가로좌표를 계산해야 합니다.
![]()
이 경우 함수는 1차 항이 없기 때문에 불완전합니다. 그에 대한
![]()
이제 우리는 가치표를 만듭니다. 이를 위해 우리는 다음의 값을 계산합니다.
![]()
상단 및 상단 주변:
![]()
![]()
![]()
![]()
![]()

마지막으로 그래프에 점을 표시하고 포물선을 그립니다.

연습 6
2차 함수와 관련된 다음 문제를 해결하세요.
제품 생산 비용은 다음 함수로 정의됩니다.
![]()
금
![]()
생산된 단위(천 단위)이고
![]()
단위의 생산 비용(수천 유로)입니다.
- 생산비용함수를 그래프로 표현합니다.
- 비용을 최소화하기 위해 몇 천 개를 생산해야 하는지 결정합니다.
이것은 이차 함수입니다. 결과적으로 이를 표현하려면 먼저 다음 공식을 사용하여 포물선 정점의 가로좌표를 찾아야 합니다.
![]()
이제 우리는 가치표를 만듭니다. 이를 위해 우리는 다음의 값을 계산합니다.
![]()
상단 및 상단 주변:
![]()
![]()
![]()
![]()
![]()
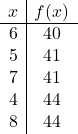
이제 그래프에 점을 표시하고 포물선을 그립니다.
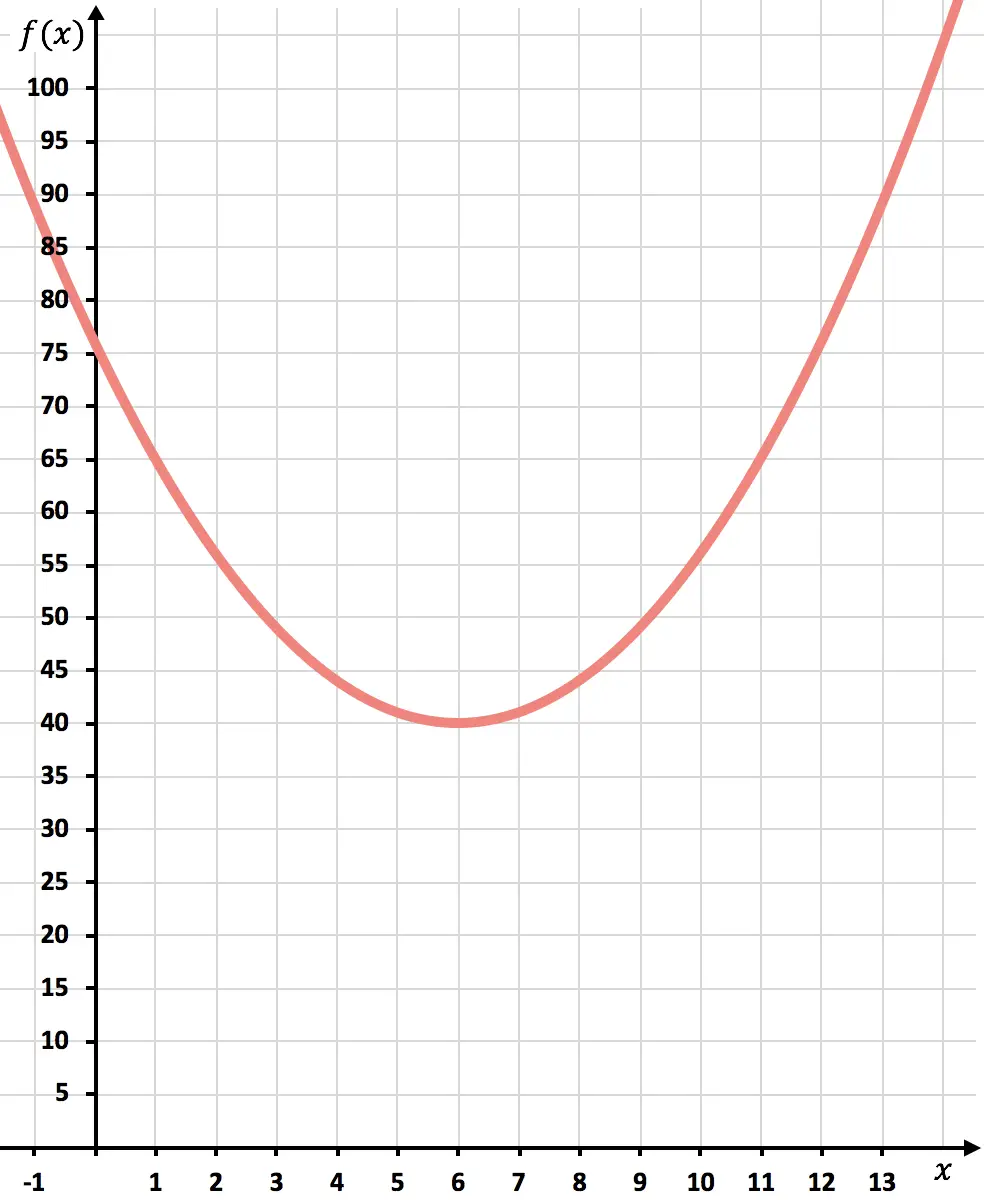
함수가 표현되면 비용이 얼마나 최소화되는지 살펴보겠습니다.
그래프에서 볼 수 있듯이 포물선 상단에서 최소 비용에 도달합니다. 왜냐하면 그것이 함수가 가장 작은 값을 취하는 곳이기 때문입니다.
결론적으로 6,000개를 생산하면 비용이 최소화된다.
연습 7
다음 이차 함수 문제를 해결하세요.
운동선수는 창던지기를 수행하며 그 궤적은 다음 함수로 표현될 수 있습니다.
![]()
금
![]()
미터는 창던지기로 덮여 있으며
![]()
높이(미터 단위)입니다.
투창이 도달할 수 있는 최대 높이는 얼마입니까?
이것은 2차 함수이므로 창던지기의 궤적은 포물선이 됩니다.
또한, 2차 항의 계수가 음수(-0.025)이므로 포물선은 역U자 모양을 가지며 가지가 아래쪽으로 향합니다. 따라서 투창은 포물선의 가장 높은 지점이 되기 때문에 상단에서 최대 높이에 도달합니다.
따라서 우리는 다음 공식을 사용하여 포물선 꼭지점의 가로좌표를 계산합니다.
![]()
그런 다음 함수를 평가하여 해당 지점에서 투창의 높이를 계산합니다.
![]()
![]()
따라서 투창이 도달할 수 있는 최대 높이는 42미터입니다.
연습 8
이차 함수에 관한 다음 문제를 해결하십시오.
회사의 생산 비용(유로)은 다음 함수로 정의됩니다.
![]()
금
![]()
생산된 단위입니다.
그리고 각 단위의 판매 가격은 €520입니다.
- 150대를 팔면 회사는 얼마나 많은 이익을 얻나요?
- 최대 이익을 얻으려면 몇 단위를 판매해야합니까?
회사는 판매된 각 단위에 대해 €520를 얻습니다. 따라서 소득을 정의하는 함수는 다음과 같습니다.
![]()
금
![]()
판매된 단위입니다.
그러나 그들은 우리에게 이익, 즉 수입에서 비용을 뺀 것에 대해 묻습니다. 따라서 회사의 이익을 설명하는 함수를 얻기 위해 수익에서 비용을 뺀 값을 뺍니다.
![]()
![]()
![]()
![]()
회사의 이익을 설명하는 함수를 알고 나면 함수 표현식에 150을 대입하여 회사가 150개를 판매하여 얻을 수 있는 이익을 계산합니다.
![Rendered by QuickLaTeX.com \begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9f5e6f3101145bcf1a2ece4db3e07c4e_l3.png)
따라서 150개를 판매하면 회사는 €12,500의 이익을 얻게 됩니다.
이 성명서는 또한 최대 이익이 달성된 단위 수를 계산하도록 요청합니다.
이익을 설명하는 함수는 2차 함수이므로 포물선 모양을 갖게 됩니다. 그리고 2차 항의 계수가 음수(-1)이므로 포물선은 역U자 모양을 갖게 되고 가지가 아래쪽으로 향하게 됩니다. 따라서 포물선의 가장 높은 지점인 상단에서 최대 이득이 만들어집니다.
따라서 우리는 다음 공식을 사용하여 포물선 꼭지점의 가로좌표를 계산합니다.
![]()
따라서 회사는 250대를 판매하여 최대의 이익을 얻을 것입니다.
반면, 보도 자료에서 요구하지 않더라도 다음 250대를 판매하여 얻을 수 있는 이익을 결정할 수 있습니다.
![]()
€