행렬에 의한 숫자의 곱셈

이 페이지에서는 숫자에 행렬을 곱하는 방법을 살펴보겠습니다. 완벽하게 이해하는 데 도움이 되는 예문도 있고, 연습할 수 있도록 문제도 풀었습니다. 또한 스칼라와 행렬의 곱의 모든 속성을 찾을 수 있습니다.

숫자에 행렬을 곱하는 방법은 무엇입니까?

숫자에 행렬을 곱 하려면 행렬의 각 요소에 숫자를 곱하세요.

예:

숫자에 행렬을 곱하는 문제 해결

연습 1:

해결책 보기

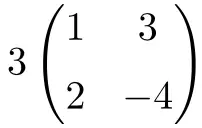
이는 스칼라와 2차 정사각 행렬의 곱입니다.

$\displaystyle 3 \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -4 \end{pmatrix} = \begin{pmatrix} 3\cdot 1 & 3\cdot 3 \\[1.1ex] 3\cdot 2 & 3\cdot (-4) \end{pmatrix} = \begin{pmatrix} \bm{3} & \bm{9} \\[1.1ex] \bm{6} & \bm{-12} \end{pmatrix}$

연습 2:

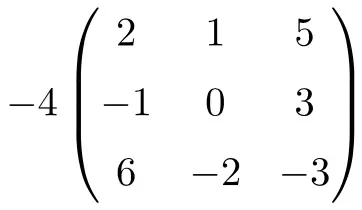
3x3 행렬에 숫자를 곱하여 단계별로 해결하는 연습, 행렬을 사용한 연산

해결책 보기

이는 3차 정사각 행렬에 의한 숫자의 곱입니다.

$\displaystyle -4 \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -1 & 0 & 3 \\[1.1ex] 6 & -2 & -3 \end{pmatrix} = \begin{pmatrix} -4 \cdot 2 & -4 \cdot 1 & -4 \cdot 5 \\[1.1ex] -4 \cdot (-1) & -4 \cdot 0 & -4 \cdot 3 \\[1.1ex] -4 \cdot 6 & -4 \cdot (-2) & -4 \cdot (-3) \end{pmatrix}= \begin{pmatrix} \bm{-8} & \bm{-4} & \bm{-20} \\[1.1ex] \bm{4} & \bm{0} & \bm {-12} \\[1.1ex] \bm{-24} & \bm{8} & \bm {12} \end{pmatrix}$

연습 3:

해결책 보기

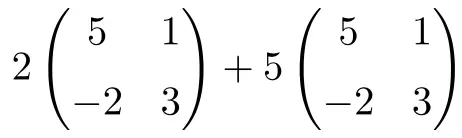
이는 숫자와 행렬의 곱과 2×2 차원 행렬의 합을 결합하는 연산입니다.

$\displaystyle 2 \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}+5\begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}$

따라서 먼저 제품을 해결해야 합니다.

$\displaystyle \begin{pmatrix} 10 & 2 \\[1.1ex] -4 & 6 \end{pmatrix}+\begin{pmatrix} 25 & 5 \\[1.1ex] -10 & 15 \end{pmatrix}$

그리고 마지막으로 결과 행렬을 추가합니다.

$\displaystyle \begin{pmatrix} \bm{35} & \bm{7} \\[1.1ex] \bm{-14} & \bm{21} \end{pmatrix}$

연습 4:

다음 행렬을 고려하십시오.

$\displaystyle A=\begin{pmatrix} 2 & -3 & 5 \\ 1 & 4 & 0 \\ -3 & 2 & -5 \end{pmatrix} \qquad B=\begin{pmatrix} 6 & 0 & 2 \\ -3 & 4 & 1 \\ 3 & 2 & 7 \end{pmatrix}$

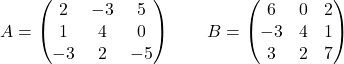
계산하다:

$\displaystyle -2A+5I-3B$

해결책 보기

이는 3×3 차원 행렬의 덧셈과 뺄셈을 스칼라 곱셈과 결합하는 연산입니다. 게다가 매트릭스는

$I$

는 주대각선이 1이고 나머지 요소가 0인 단위 행렬입니다.

$\displaystyle -2\begin{pmatrix} 2 & -3 & 5 \\[1.1ex] 1 & 4 & 0 \\[1.1ex] -3 & 2 & -5 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} -3 \begin{pmatrix} 6 & 0 & 2 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 3 & 2 & 7 \end{pmatrix}$

따라서 먼저 곱셈을 수행합니다.

$\displaystyle \begin{pmatrix} -4 & 6 & -10 \\[1.1ex] -2 & -8 & 0 \\[1.1ex] 6 & -4 & 10 \end{pmatrix}+\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

처음 두 개의 행렬을 추가합니다.

$\displaystyle \begin{pmatrix} 1 & 6 & -10 \\[1.1ex] -2 & -3 & 0 \\[1.1ex] 6 & -4 & 15 \end{pmatrix}-\begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

마지막으로 행렬의 뺄셈을 수행합니다.

$\displaystyle \begin{pmatrix} \bm{-17} & \bm{6} & \bm{-16} \\[1.1ex] \bm{7} & \bm{-15} & \bm{-3} \\[1.1ex] \bm{-3} & \bm{-10} & \bm{-6} \end{pmatrix}$

행렬 스칼라 곱에 대한 이러한 연습이 도움이 되었다면 더 이상 반복되는 두 가지 유형의 행렬 연산인 행렬의 덧셈 과 행렬의 곱 에 대한 단계별 연습을 통해 주저하지 말고 연습해 보세요.

행렬에 의한 숫자의 곱의 속성

잘 아시 다시피 행렬에는 정사각형 행렬, 삼각 행렬, 단위 행렬 등 다양한 유형이 있습니다. 그러나 다행스럽게도 행렬에 의한 숫자 곱의 모든 속성은 모든 종류의 행렬에 유효합니다.

스칼라와 행렬 사이의 곱셈의 속성은 다음과 같습니다.

연관 속성:

$a \cdot (b \cdot A) = (a \cdot b) \cdot A$

다음 두 연산을 살펴보세요. 2와 3을 어떻게 곱하든 동일한 결과를 제공하기 때문입니다.

$\displaystyle 2 \cdot \left(3 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} \right) =2 \cdot \begin{pmatrix} 3 & 0 \\[1.1ex] 6 & -3 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

$\displaystyle (2 \cdot 3) \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} =6 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

스칼라 덧셈에 관한 분배법칙 :

$(a+b) \cdot A = a \cdot A+ b \cdot A$

아래 예에서 볼 수 있듯이 먼저 1+2를 더한 다음 행렬로 곱하거나 행렬에 별도로 1과 2를 곱한 다음 결과를 더해도 동일합니다.

$\displaystyle (1 + 2) \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} =3 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

$\displaystyle 1 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4\end{pmatrix} = \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5\\[1.1ex] -2 & -4 \end{pmatrix} + \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & 10 \\[1.1ex] -4 & -8\end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

행렬 덧셈에 관한 분배법칙 :

$a \cdot \left(A + B \right) = a \cdot A + a \cdot B$

즉, 두 개의 수학적 행렬을 더한 다음 숫자로 곱하는 것은 두 개의 행렬에 동일한 숫자를 개별적으로 곱한 다음 결과를 더하는 것과 같습니다. 아래 예에서 다음을 확인할 수 있습니다.

$\displaystyle 4 \cdot \left( \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+\begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} \right) =4 \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 6 & 3 \end{pmatrix}= \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

$\displaystyle 4 \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+ 4 \cdot \begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} = \begin{pmatrix} 12 & -8 \\[1.1ex] 24 & -4 \end{pmatrix}+\begin{pmatrix} -4 & 12 \\[1.1ex] 0 & 16 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

중립 요소의 속성:

$1 \cdot A = A$

따라서 행렬에 1을 곱할 때 행렬을 수정하지 않습니다.

$\displaystyle 1 \cdot \begin{pmatrix} 5 & -4 & 0 \\[1.1ex] 1 & 3 & -3 \\[1.1ex] 2 & 9 & 4 \end{pmatrix}=\begin{pmatrix} \bm{5} & \bm{-4} & \bm{0} \\[1.1ex] \bm{1} & \bm{3} & \bm{-3} \\[1.1ex] \bm{2} & \bm{9} & \bm{4} \end{pmatrix}$

이것들은 모두 스칼라와 행렬의 곱의 속성이므로 이것이 이 글의 끝입니다. 이 내용이 마음에 들었기를 바라며, 무엇보다도 행렬을 사용하여 숫자의 곱셈을 푸는 방법을 배웠기를 바랍니다.

반면, 곱셈과 연결되어 있고 매우 유용한 다른 행렬 연산은 거듭제곱입니다. 여기서는 행렬이 무엇인지, 행렬의 힘을 해결하는 방법을 배울 수 있는 페이지를 남겨드립니다. 혹시 궁금하신가요?

숫자에 행렬 곱하기

숫자에 행렬을 곱하는 방법은 무엇입니까?

예:

숫자에 행렬을 곱하는 문제 해결

연습 1:

연습 2:

연습 3:

연습 4:

행렬에 의한 숫자의 곱의 속성

댓글 달기 댓글 취소