이 페이지에서는 2×2, 3×3, 4×4 등의 차원 행렬을 곱하는 방법을 살펴보겠습니다. 예제를 통해 행렬 곱셈 절차를 단계별로 설명하고, 연습할 수 있도록 해결된 연습 문제도 찾아볼 수 있습니다. 마지막으로 두 행렬을 곱할 수 없는 경우와 이 행렬 연산의 모든 속성을 학습합니다.
두 행렬을 곱하는 방법은 무엇입니까?
예를 들어 두 행렬의 곱셈을 수행하는 절차를 살펴보겠습니다.
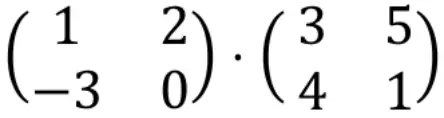
행렬 곱셈을 계산하려면 왼쪽 행렬의 행 에 오른쪽 행렬의 열을 곱해야 합니다.
따라서 먼저 첫 번째 행과 첫 번째 열을 곱해야 합니다. 이를 위해 첫 번째 행의 각 요소와 첫 번째 열의 각 요소를 하나씩 곱하고 결과를 더합니다. 따라서 이 모든 것이 결과 배열의 첫 번째 행의 첫 번째 요소가 됩니다. 절차를 살펴보십시오.
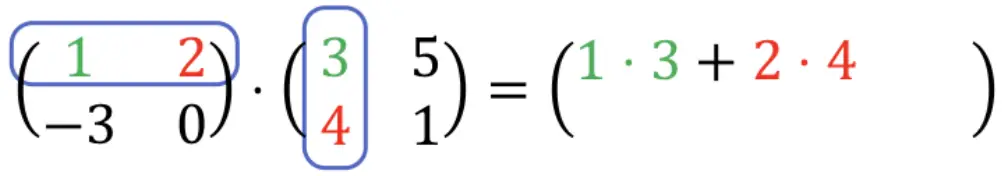
1 ⋅ 3 + 2 ⋅ 4 = 3 + 8 = 11. 따라서:
이제 첫 번째 행에 두 번째 열을 곱해야 합니다. 따라서 절차를 반복합니다. 첫 번째 행의 각 요소에 두 번째 열의 각 요소를 하나씩 곱하고 결과를 더합니다. 그리고 이 모든 것은 결과 배열의 첫 번째 행의 두 번째 요소가 됩니다.
1 ⋅ 5 + 2 ⋅ 1 = 5 + 2 = 7. 따라서:
결과 행렬의 첫 번째 행을 채우고 나면 두 번째 행으로 이동합니다. 따라서 절차를 반복하여 두 번째 행에 첫 번째 열을 곱합니다. 두 번째 행의 각 요소에 첫 번째 열의 각 요소를 1씩 곱하고 결과를 더합니다.
-3 ⋅ 3 + 0 ⋅ 4 = -9 + 0 = -9. 아직:
마지막으로 두 번째 행에 두 번째 열을 곱합니다. 항상 동일한 절차를 사용합니다. 두 번째 행의 각 요소에 두 번째 열의 각 요소를 하나씩 곱하고 결과를 추가합니다.
-3 ⋅ 5 + 0 ⋅ 1 = -15 + 0 = -15. 아직:
그리고 여기서 두 행렬의 곱셈이 끝납니다. 보시다시피 행과 열을 곱해야 하며 항상 동일한 절차를 반복해야 합니다. 행의 각 요소에 열의 각 요소를 하나씩 곱하고 결과를 더합니다.
해결 행렬 곱셈 연습
연습 1
다음 매트릭스 곱을 푼다:
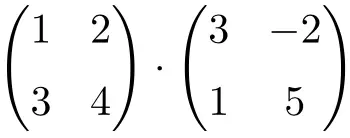
이는 2차 행렬의 곱입니다:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-747926b92c1d388c1150613b0f471d7e_l3.png)
행렬 곱을 풀려면 왼쪽 행렬의 행과 오른쪽 행렬의 열을 곱해야 합니다.
따라서 먼저 첫 번째 행에 첫 번째 열을 곱합니다. 이를 위해 첫 번째 행의 각 요소와 첫 번째 열의 각 요소를 하나씩 곱하고 결과를 더합니다. 그리고 이 모든 것은 결과 배열의 첫 번째 행의 첫 번째 요소가 됩니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eff23eaf91738d6ffb383949e4b70856_l3.png)
이제 첫 번째 행에 두 번째 열을 곱하여 결과 행렬의 첫 번째 행의 두 번째 요소를 얻습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-558838bcc38efc1aeeaf298d3e7151dc_l3.png)
두 번째 행으로 이동하여 두 번째 행에 첫 번째 열을 곱합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-daab54a49cc53c320bb2965f691fd7ed_l3.png)
마지막으로 두 번째 행에 두 번째 열을 곱하여 테이블의 마지막 요소를 계산합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a85e0d62a0db18c7712fd1b354f92bd5_l3.png)
따라서 행렬 곱셈의 결과는 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76f1283db0175bc1a95b0a10c8961761_l3.png)
연습 2
다음 2×2 정사각 행렬 곱셈의 결과를 구합니다.
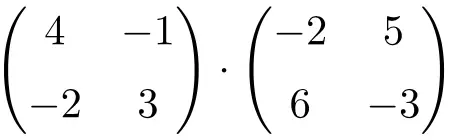
2×2 차원의 행렬의 곱입니다.
곱셈을 풀려면 왼쪽 행렬의 행과 오른쪽 행렬의 열을 곱해야 합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc7217dab49f67df2a9d2abc561baf9d_l3.png)
연습 3
다음 3×3 행렬 곱셈을 계산합니다.
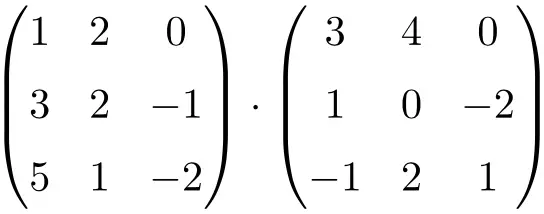
3×3 행렬 곱셈을 수행하려면 왼쪽 행렬의 행과 오른쪽 행렬의 열을 곱해야 합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef6ee7bb6e4ac095a9fd51a545b163b0_l3.png)
연습 4
주어진 매트릭스
![]()
:
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-27365f9993caf4fcdb747352e4ae539d_l3.png)
계산하다:
![]()
먼저 전치 행렬을 계산하겠습니다.
![]()
곱셈을 하려고요. 그리고 전치 행렬을 만들려면 행을 열로 변경해야 합니다. 즉, 행렬의 첫 번째 행은 행렬의 첫 번째 열이 되고, 행렬의 두 번째 행은 행렬의 두 번째 열이 됩니다. 아직:
![Rendered by QuickLaTeX.com \displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac4785c47f2e48e15b3d98ba426848b6_l3.png)
따라서 행렬 연산은 다음과 같이 유지됩니다.
![Rendered by QuickLaTeX.com \displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9513fa8cc6996e18e3cf287f0210817a_l3.png)
이제 계산을 할 수 있습니다. 우리는 먼저 계산합니다
![]()
(먼저 계산할 수도 있지만
![]()
):
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae5e95f09aedac8f0861bf13fb9c78a4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-24c003b8da1081d6ca494adc3356b06b_l3.png)
그리고 마지막으로 행렬의 곱을 해결합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-0eb8f1817f0163a82ae39cc6c81d478e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-33533be747b72497915048e486d16541_l3.png)
연습 5
다음 행렬을 고려하십시오.
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e26aec2eee6bcae0e344682d20038f2_l3.png)
계산하다:
![]()
이는 2차 행렬 곱셈과 뺄셈을 결합하는 연산입니다.
![Rendered by QuickLaTeX.com \displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-43f79f2d970bb02caaeddec34d5ad2a1_l3.png)
먼저 왼쪽의 곱셈을 계산합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-05ff586671fb0af274884169c54e5817_l3.png)
![Rendered by QuickLaTeX.com \displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-43c234a2d7aa4f9dcaf3140f617480f1_l3.png)
이제 오른쪽의 곱셈을 푼다:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-552309dd1be2f69bb72633539809283b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eeac84965cc522402e869234a841ba67_l3.png)
그리고 마지막으로 행렬을 뺍니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =](https://mathority.org/wp-content/ql-cache/quicklatex.com-faefbc14fc49439616b3d131243eba79_l3.png)
![Rendered by QuickLaTeX.com \displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50bac6ac99e1cf6e4b77a1a8718f9fe4_l3.png)
언제 두 행렬을 곱할 수 없나요?
모든 행렬을 곱할 수 있는 것은 아닙니다. 두 행렬을 곱하려면 첫 번째 행렬의 열 수가 두 번째 행렬의 행 수와 일치해야 합니다.
예를 들어, 첫 번째 행렬에는 3개의 열이 있고 두 번째 행렬에는 2개의 행이 있으므로 다음 곱셈을 수행할 수 없습니다.
![Rendered by QuickLaTeX.com \displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8314f9238afb3676bee5c9000c02752_l3.png)
하지만 순서를 반대로 하면 곱해질 수 있습니다. 첫 번째 행렬에는 두 개의 열이 있고 두 번째 행렬에는 두 개의 행이 있기 때문입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-37d01cc99b578d3756312c3e6ff12cae_l3.png)
행렬 곱셈 속성
이러한 유형의 행렬 연산에는 다음과 같은 특징이 있습니다.
- 행렬 곱셈은 연관적입니다.
![]()
- 행렬 곱셈에는 분배 속성도 있습니다.
![]()
- 행렬의 곱은 교환적이지 않습니다.
![]()
예를 들어, 다음 행렬 곱셈은 결과를 제공합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3e780b321b160ad4a612e608199a374b_l3.png)
그러나 행렬의 곱셈 순서를 바꾸면 결과가 달라집니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-177d78a209e5d9e18828617e4913176d_l3.png)
- 또한 단위 행렬을 곱한 모든 행렬은 동일한 행렬이 됩니다. 이를 곱셈 항등 속성이라고 합니다.
![]()
![]()
예를 들어:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c1e72173419eb76554256cf6ccd0d2f_l3.png)
- 마지막으로 이미 짐작할 수 있듯이 제로 행렬을 곱한 모든 행렬은 제로 행렬과 같습니다. 이것을 0의 곱셈법칙이라고 합니다:
![]()
![]()
예를 들어:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3152d82054a80d61d548e969290aea4c_l3.png)