헤세 행렬(또는 헤세) -

이 페이지는 확실히 존재하는 헤세 행렬에 대한 가장 완전한 설명입니다. 여기에서는 헤세 행렬의 개념과 이를 계산하는 방법을 예제를 통해 설명하고 연습할 수 있는 몇 가지 해결된 연습 문제도 있습니다. 또한 다변수 함수의 최대값과 최소값이 어떻게 계산되는지, 그리고 그것이 오목 함수인지 볼록 함수인지도 배울 수 있습니다. 마지막으로 헤세 행렬 유틸리티와 애플리케이션도 찾을 수 있습니다.

헤세 행렬이란 무엇입니까?

헤시안(또는 헤시안) 행렬의 정의는 다음과 같습니다.

헤세 행렬(Hessian Matrix)은 n 변수 함수의 부분 2차 도함수로 구성된 n × n 차원의 정사각 행렬입니다.

이 행렬은 헤세 행렬(Hessian)이라고도 알려져 있으며 일부 수학 책에서는 판별 행렬(Discriminant)이라고 불리기도 합니다. 그러나 이를 호출하는 가장 일반적인 방법은 헤세 행렬(Hessian Matrix)입니다.

따라서 헤세 행렬의 공식은 다음과 같습니다.

따라서 헤세 행렬은 항상 함수의 변수 수와 차원이 같은 정사각 행렬이 됩니다. 예를 들어, 함수에 3개의 변수가 있는 경우 헤세 행렬의 차원은 3×3입니다.

또한 Schwarz의 정리 (또는 Clairaut의 정리)는 미분의 순서가 중요하지 않다고 말합니다. 즉, 변수에 대해 부분적으로 먼저 파생됩니다.

$x_1$

그런 다음 변수와 관련하여

$x_2$

부분적으로 차별화되는 셈이다.

$x_2$

그럼 존경해

$x_1$

$\displaystyle \cfrac{\partial^2 f}{\partial x_i\partial x_j} = \cfrac{\partial^2 f}{\partial x_j\partial x_i}$

따라서 헤세 행렬은 대칭 행렬, 즉 주대각선을 축으로 하는 대칭 행렬입니다.

흥미롭게도 헤세 행렬은 선형 대수학 분야에 매우 중요한 공헌을 한 19세기 독일 수학자 루트비히 오토 헤세(Ludwig Otto Hesse)의 이름을 따서 명명되었습니다.

헤세 행렬 계산의 예

2 × 2 차원의 헤세 행렬을 찾는 방법의 예를 살펴보겠습니다.

다음 함수의 점 (1,0)에서 헤세 행렬을 계산합니다.

$\displaystyle f(x,y)=y^4+x^3+3x^2+ 4y^2 -4xy -5y +8$

먼저, 1차 편도함수를 계산해야 합니다.

$\displaystyle \cfrac{\partial f}{\partial x} = 3x^2 +6x -4y$

$\displaystyle \cfrac{\partial f}{\partial y} = 4y^3+8y -4x -5$

1차 도함수를 이미 알고 나면 모든 2차 편도함수를 계산합니다.

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 6x +6$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =12y^2 +8$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}= -4$

따라서 이제 2 × 2 행렬에 대한 공식에서 헤세 행렬을 찾을 수 있습니다.

$\displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}$

$\displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}$

따라서 점 (1,0)에서 평가된 헤세 행렬은 다음과 같습니다.

$\displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}$

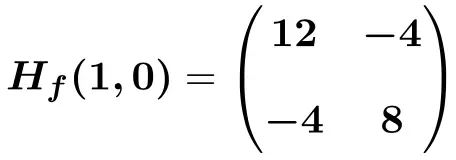
헤세 행렬의 문제 해결

연습 1

점 (1,1)에서 2개의 변수를 사용하여 다음 함수의 헤세 행렬을 계산합니다.

$\displaystyle f(x,y)=x^2y+y^2x$

해결책 보기

먼저, 함수의 1차 편도함수를 찾아야 합니다.

$\displaystyle \cfrac{\partial f}{\partial x} = 2xy+y^2$

$\displaystyle \cfrac{\partial f}{\partial y} = x^2+2yx$

이미 1차 도함수를 계산한 후에는 모든 2차 편도함수를 푸는 작업을 진행합니다.

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 2y$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =2x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}=2x+2y$

따라서 헤세 행렬은 다음과 같이 정의됩니다.

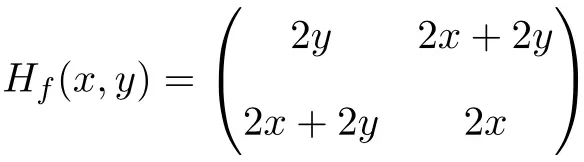
마지막으로 남은 것은 점 (1,1)에서 헤세 행렬을 평가하는 것입니다.

$\displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}$

연습 2

두 변수의 다음 함수의 점 (1,1)에서 헤세 행렬을 계산합니다.

$\displaystyle f(x,y)= e^{y\ln x}$

해결책 보기

먼저, 함수의 1차 편도함수를 계산해야 합니다.

$\displaystyle \cfrac{\partial f}{\partial x} = e^{y\ln x} \cdot \cfrac{y}{x}$

$\displaystyle \cfrac{\partial f}{\partial y} = e^{y\ln x} \cdot \ln x$

1차 도함수를 얻은 후에는 함수의 2차 편도함수를 계산합니다.

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = e^{y\ln x} \cdot \cfrac{y^2}{x^2} - e^{y\ln x} \cdot \cfrac{y}{x^2}$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =e^{y\ln x} \cdot \ln ^2 x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =e^{y\ln x} \cdot \cfrac{y}{x}\cdot \ln x + e^{y\ln x}\cdot \cfrac{1}{x}$

따라서 함수의 헤세 행렬은 2×2 차원의 정사각 행렬입니다.

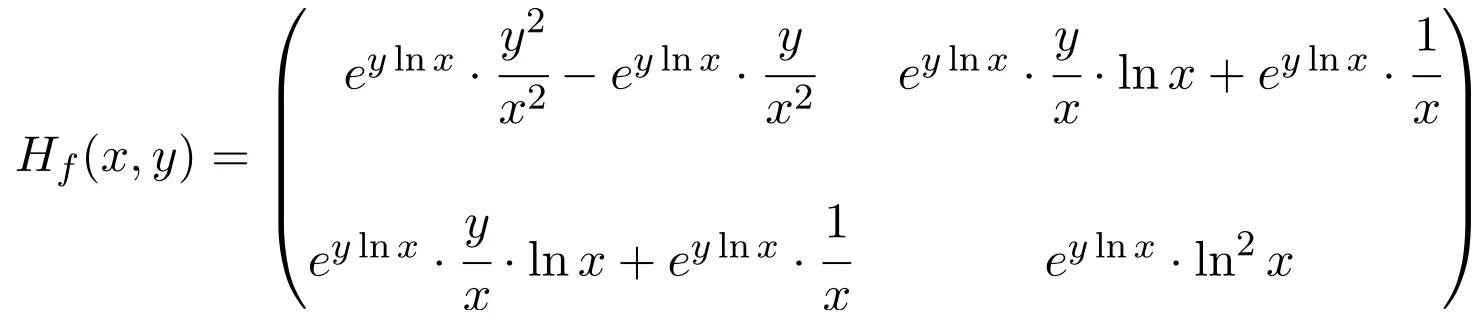
마지막으로 남은 것은 점 (1,1)에서 헤세 행렬을 평가하는 것입니다.

$\displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}$

연습 3

해당 지점에서 헤세 행렬을 구합니다.

$(0,1,\pi)$

3개의 변수가 있는 다음 함수:

$\displaystyle f(x,y,z)= e^{-x}\cdot \text{sen}(yz)$

해결책 보기

먼저, 함수의 1차 편도함수를 계산합니다.

$\displaystyle \cfrac{\partial f}{\partial x} = -e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial f}{\partial y} = ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial f}{\partial z} = ye^{-x}\cdot \text{cos}(yz)$

1차 도함수를 얻은 후에는 함수의 2차 편도함수를 계산합니다.

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =-ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x} =-ye^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =-z^2e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial z \partial y} =e^{-x}\cdot \text{cos}(yz)-yze^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} = -y^2e^{-x}\cdot \text{sen}(yz)$

따라서 함수의 헤세 행렬은 3×3 차원의 정사각 행렬입니다.

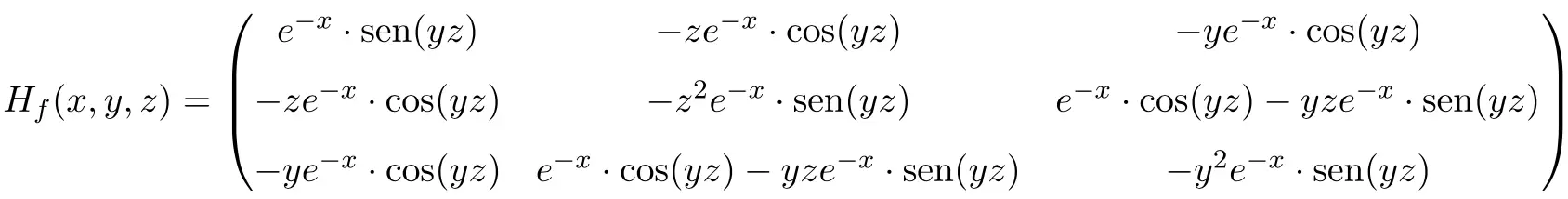
마지막으로 해당 시점에서 변수를 해당 값으로 대체합니다.

$(0,1,\pi):$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}$

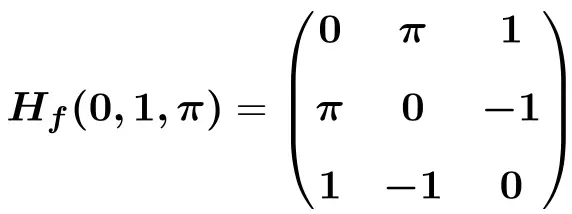
3x3 차원의 헤세 행렬(Hessian Matrix) 또는 헤세 행렬(Hessian Matrix)을 단계별로 풀어내는 연습

연습 4

4개의 변수를 사용하여 다음 함수의 점 (2,-1,1,-1)에서 헤세 행렬을 결정합니다.

$\displaystyle f(x,y,z,w)= 2x^3y^4zw^2 - 2y^3w^4+ 3x^2z^2$

해결책 보기

첫 번째 단계는 함수의 1차 편도함수를 찾는 것입니다.

$\displaystyle \cfrac{\partial f}{\partial x} =6x^2y^4zw^2 + 6xz^2$

$\displaystyle \cfrac{\partial f}{\partial y} =8x^3y^3zw^2 - 6y^2w^4$

$\displaystyle \cfrac{\partial f}{\partial z} = 2x^3y^4w^2 + 6x^2z$

$\displaystyle \cfrac{\partial f}{\partial w} =4x^3y^4zw - 8y^3w^3$

이제 우리는 함수의 2차 편도함수를 푼다:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =12xy^4zw^2 + 6z^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x}=24x^2y^3zw^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x}=6x^2y^4w^2 + 12xz$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial w} = \cfrac{\partial^2 f}{\partial w \partial x}=12x^2y^4zw$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =24x^3y^2zw^2 - 12yw^4$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial y \partial z}=8x^3y^3w^2$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial w} = \cfrac{\partial^2 f}{\partial w \partial y}=16x^3y^3zw - 24y^2w^3$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} =6x^2$

$\displaystyle \cfrac{\partial^2 f}{\partial z \partial w} = \cfrac{\partial^2 f}{\partial w \partial z}=4x^3y^4w$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 w} =4x^3y^4z - 24y^3w^2$

따라서 모든 편도함수를 풀어 얻은 4×4 헤세 행렬의 표현은 다음과 같습니다.

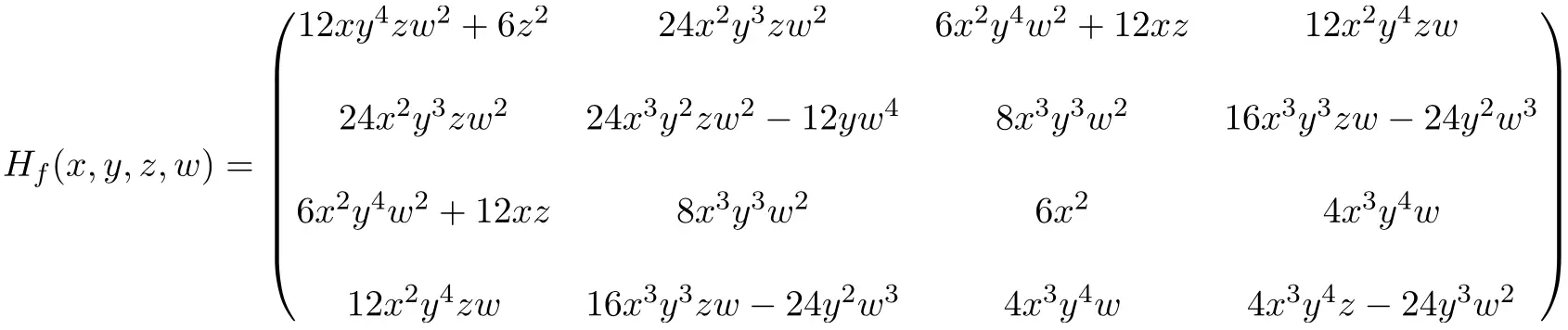
마지막으로, 각각의 포인트 값(2,-1,1,-1)을 미지수로 대체하고 계산을 수행합니다.

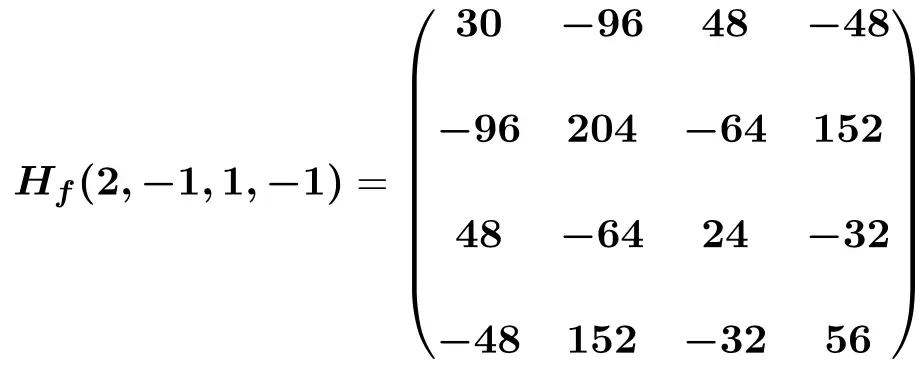
4x4 차원의 Hessian 또는 Hessian 행렬을 단계별로 해결하는 연습

헤세 행렬이 양수, 음수 또는 부정수인지 어떻게 알 수 있나요?

나중에 살펴보겠지만, 헤세 행렬이 양의 준정부호, 양의 준정부호, 음의 준정부호, 음의 정부호, 부정호 행렬인지 아는 것은 매우 유용합니다. 그럼 어떻게 알 수 있는지 살펴보겠습니다.

고유값(또는 고유값)의 기준

어떤 유형의 행렬인지 알 수 있는 한 가지 방법은 헤세 행렬의 고유값(또는 고유값)을 살펴보는 것입니다.

헤세 행렬은 0보다 크거나 같은 고유값(또는 고유값)을 갖는 경우 양의 준정부호 입니다. 즉, 양의 고유값이 있고 적어도 하나는 0과 같습니다.

$\lambda \geq 0$

헤세 행렬은 모든 고유값(또는 고유값)이 전적으로 0(양수)보다 큰 경우 양의 정부호 행렬 입니다.

$\lambda > 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”></p> </p> <ul> <li> 헤세 행렬은 고유값(또는 고유값)이 0 이하인 경우 음의 <span style=$ 준정부호입니다 . 즉, 음의 고유값이 있고 적어도 하나는 0과 같습니다.

$\lambda \leq 0$

헤세 행렬은 모든 고유값(또는 고유값)이 0(음수)보다 작은 경우 음의 정부호 행렬 입니다.

$\lambda < 0$

헤세 행렬은 양수 및 음수 고유값(또는 고유값)을 갖는 경우 정의되지 않습니다 .

$\lambda > 0 \qquad \lambda <0$

실베스터 기준

헤세 행렬이 어떤 유형인지 알 수 있는 또 다른 방법은 실베스터의 기준을 사용하는 것입니다. 하지만 이 정리는 양의 정부호, 음의 정부호 또는 부정호인지만 알 수 있습니다. 그러나 때로는 계산이 일반적으로 더 쉽기 때문에 사용하는 것이 훨씬 더 빠를 수도 있습니다.

따라서 실베스터 기준은 다음과 같습니다.

헤세 행렬의 모든 주요 마이너가 0보다 큰 경우 이는 양의 정부호 행렬입니다.

짝수 인덱스를 갖는 헤세 행렬의 주요 마이너가 0보다 크고 홀수 인덱스를 갖는 주요 마이너가 0보다 작은 경우 이는 음의 정부호 행렬 입니다.

헤세 행렬의 모든 주요 부차 요소가 0이 아니고 이전 두 조건 중 어느 것도 충족되지 않으면 이는 무한 행렬입니다.

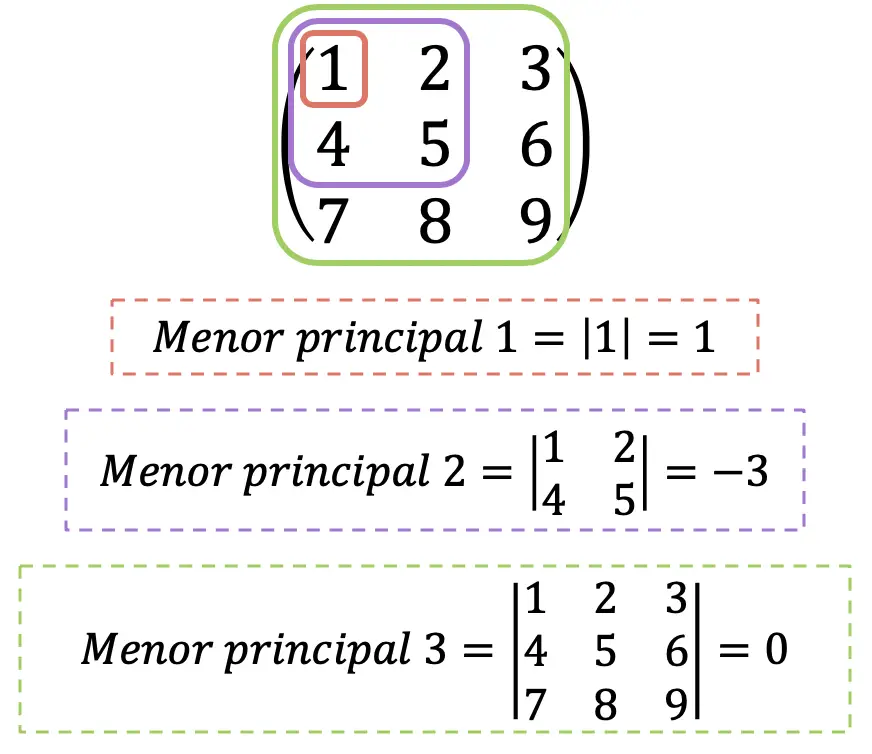
분명히, 헤세 행렬의 최대 주 마이너는 행렬식과 항상 일치합니다. 단지 정보 제공의 목적으로, 헤세 행렬의 행렬식을 “헤세 행렬”이라고도 부르지만, 여기서는 혼동을 피하기 위해 그렇게 하지 않겠습니다.

헤세 행렬을 사용하여 함수의 최대값 또는 최소값을 계산하는 방법

헤세 행렬을 계산하는 방법을 알게 되면 아마도 궁금할 것입니다. 이 행렬은 어디에 사용됩니까?

헤세 행렬의 응용 중 하나는 둘 이상의 변수를 갖는 함수의 최대값 또는 최소값을 찾는 것입니다. 다음은 최대값과 최소값을 계산하는 방법에 대한 단계별 설명입니다.

먼저 다변수 함수의 임계점을 계산합니다. 이를 위해 함수의 기울기 또는 야코비안 행렬을 계산하고 이를 0으로 설정한 후 방정식을 풉니다.
헤세 행렬이 계산됩니다.
1단계에서 찾은 임계점은 헤세 행렬로 대체됩니다. 따라서 우리는 임계점이 기능하는 만큼 많은 헤세 행렬을 얻을 것입니다.
각 헤세 행렬이 어떤 행렬인지 살펴보겠습니다. 즉, 우리는 그것이 양의 정부호, 음의 정부호, 부정확한지 등을 살펴봅니다.
- 헤세 행렬이 양의 정부호 행렬인 경우 임계점은 함수의 상대적 최소값 입니다.
- 헤세 행렬이 음의 정부호 행렬인 경우 임계점은 함수의 상대 최대값 입니다.
- 헤세 행렬이 정의되지 않은 경우 임계점 은 안장점입니다.

다변수 함수의 최대값과 최소값 계산 예

이것이 어떻게 수행되는지 확인하기 위해 헤세 행렬을 사용하여 함수의 상대 극값을 계산하고 분류하는 예는 다음과 같습니다.

다음 다변수 함수의 모든 상대 극값을 찾습니다.

$\displaystyle f(x,y)=x^2-y^2+2xy+ 4x-4y$

가장 먼저 해야 할 일은 함수의 야코비안 행렬을 계산하는 것입니다. 이 경우 스칼라 함수이기 때문에 기울기와 일치합니다.

$\displaystyle \nabla f (x,y)=(2x+2y+4 \ , \ -2y+2x-4 )$

이제 임계점을 결정해야 합니다. 이를 위해 얻은 방정식을 0으로 동일화하고 방정식 시스템을 풀어야 합니다.

$\displaystyle \nabla f (x,y)=0$

$\displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)$

그래서 우리가 찾은 임계점은 (0,-2)입니다.

함수의 임계점을 찾으면 헤세 행렬을 계산해야 합니다.

$\displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

그리고 분명히 임계점에서 평가된 헤세 행렬은 동일합니다.

$\displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

어떤 유형의 행렬인지 확인하기 위해 실베스터 기준을 사용하겠습니다. 따라서 우리는 매트릭스의 주요 마이너를 해결합니다.

$\displaystyle \begin{vmatrix}2 \end{vmatrix} = 2$

$\displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8$

주 단조 1(홀수)은 양수이고 주요 단조 2(짝수)는 음수이므로 실베스터 기준에 따르면 이는 무한 행렬입니다. 따라서 임계점(0,-2)은 안장점입니다.

헤세 행렬을 사용하여 함수의 오목성 또는 볼록성 결정

헤세 행렬의 또 다른 용도는 함수가 오목인지 볼록인지를 아는 것입니다. 그리고 이는 다음 정리에 따라 결정될 수 있습니다.

$A \subseteq \mathbb{R}^n$

오픈 세트와

$f \colon A \to \mathbb{R}$

2차 도함수가 연속인 함수, 오목함과 볼록함은 헤시안 행렬로 정의됩니다.

기능
$f$

전체적으로 볼록 하다

$A$

헤세 행렬이 집합의 모든 점에서 양의 준정부호인 경우에만 가능합니다.
기능
$f$

전체적으로 볼록하다

$A$

헤세 행렬이 집합의 모든 점에서 양의 정부호인 경우에만 가능합니다.

✓ 그러므로 만일

$f$

는 야코비 행렬도 사라지는 지점에서 볼록 함수이며, 이 지점은 지역 최소값 입니다.

기능
$f$

전체적으로 오목하다

$A$

헤세 행렬이 집합의 모든 점에서 음의 준확정인 경우에만 가능합니다.
기능
$f$

전체적으로 엄격하게 오목 하다

$A$

헤세 행렬이 집합의 모든 점에서 음의 정부호인 경우에만 가능합니다.

✓ 그러므로 만일

$f$

는 야코비 행렬도 사라지는 지점에서 오목한 함수이며, 이 지점은 로컬 최대값 입니다.

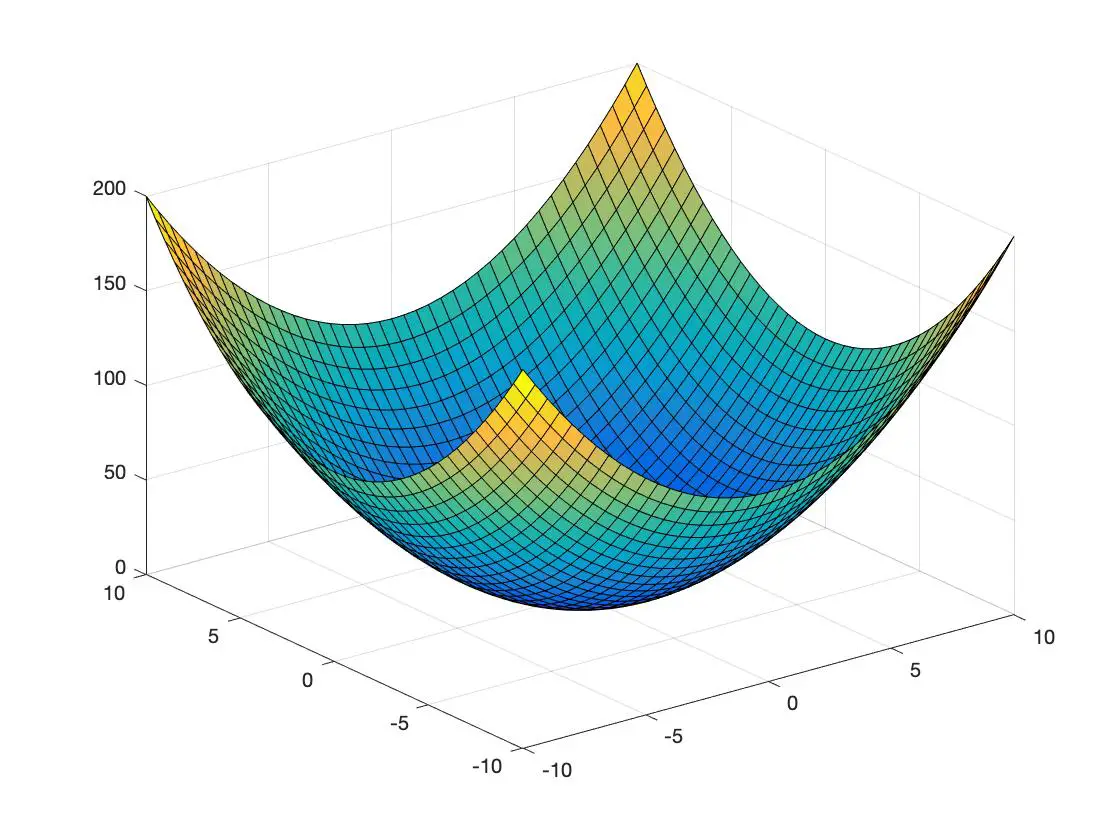
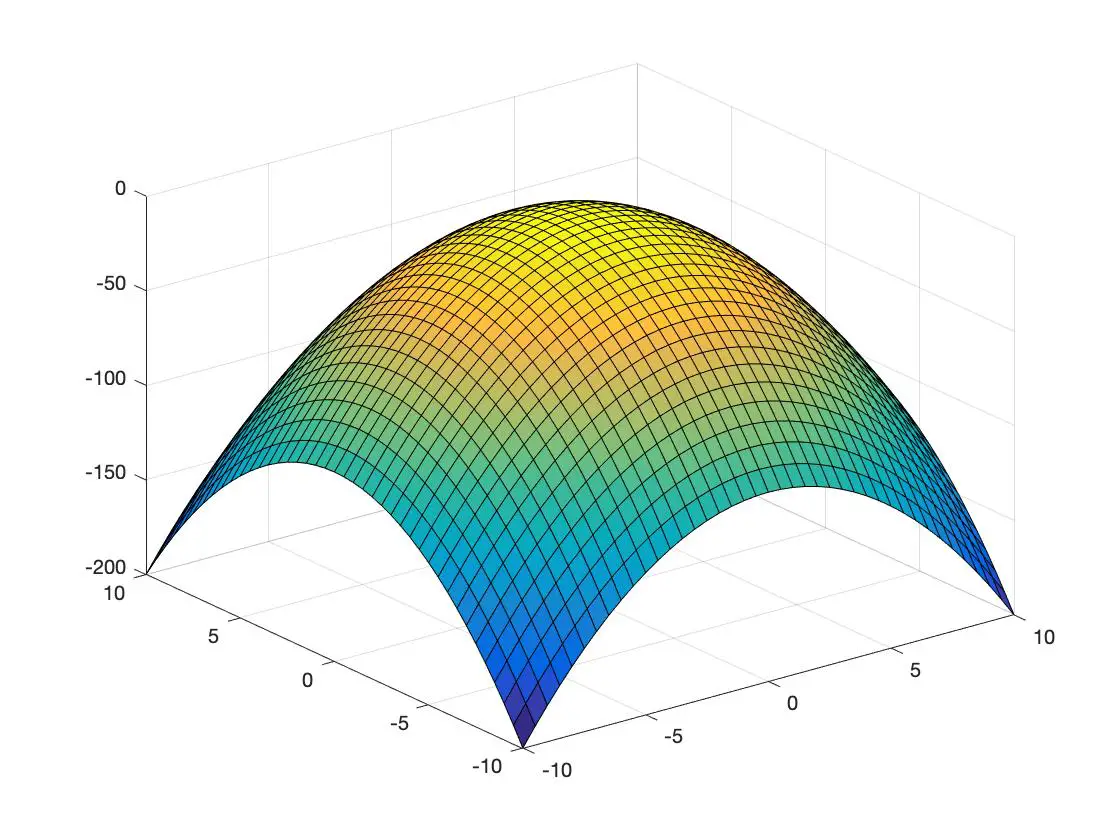
아래에는 3차원 공간에 표현된 볼록 함수와 오목 함수의 예가 있습니다.

볼록함수

오목함수

이미지에 빈 ALT 속성이 있습니다. 파일 이름은 함수의 요철과 볼록-with-the-hessian-matrix-1024x768.jpg입니다.

헤세 행렬의 더 많은 응용

헤세 행렬의 주요 용도는 우리가 이미 본 것이지만 다른 용도도 있습니다. 가장 궁금한 분들을 위해 아래에서 설명하겠습니다.

테일러 다항식

점에서 2개 이상의 변수를 갖는 함수에 대한 테일러 다항식 의 전개

$a$

다음과 같이 시작합니다:

$\displaystyle T(x) = f(a) + (x-a)^T \nabla f(a) + \frac{1}{2}(x-a)^T \operatorname{H}_f(a)(x-a) + \ldots$

보시다시피, 테일러 확장의 2차 항은 다항식의 확장 지점에서 평가된 헤세 행렬에 의해 제공됩니다.

경계가 있는 삼베 매트릭스

헤세 행렬의 또 다른 용도는 다변량 함수의 최소값과 최대값을 계산하는 것입니다.

$f(x,y)$

다른 역할로 제한됨

$g(x,y)$

. 이 문제를 해결하기 위해 유계 헤세 행렬(Bounded Hessian Matrix)을 사용하고 다음 절차를 따른다.

1단계: 다음 식으로 정의되는 라그랑주 함수가 계산됩니다.

$\displaystyle L(x,y,\lambda) = f(x,y)+ \lambda \cdot g(x,y)$

2단계: 라그랑주 함수의 임계점을 찾습니다. 이를 위해 라그랑주 함수의 기울기를 계산하고 방정식을 0으로 설정하고 방정식을 풉니다.

$\displaystyle \nabla L = 0$

$\displaystyle \cfrac{\partial L}{\partial x} = 0 \qquad \cfrac{\partial L}{\partial y}=0 \qquad \cfrac{\partial L}{\partial \lambda}=0$

3단계: 찾은 각 점에 대해 다음 행렬로 정의되는 유계 헤세 행렬을 계산합니다.

$\displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}$

4단계: 각 임계점에 대해 그것이 최대인지 최소인지 결정합니다.

이는 함수의 로컬 최대값이 됩니다.
$f$

기능 제약 하에서

$g$

임계점에서 평가된 경계가 있는 헤세 행렬의 마지막 nm (여기서 n 은 변수 수이고 m은 제약 조건 수) 주요 마이너가 음수 부호로 시작하는 교대 부호를 갖는 경우.

이는 함수의 로컬 최소값이 됩니다.
$f$

기능 제약 하에서

$g$

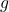
임계점에서 평가된 날카로운 헤세 행렬의 마지막 nm (여기서 n 은 변수 수이고 m은 제약 조건 수) 주요 마이너가 모두 음수 부호를 갖는 경우.

하나의 제한된 기능에 대한 다른 제한된 기능의 상대적 최소값 또는 최대값은 제한되지 않은 기능에 대해 반드시 그렇게 될 필요는 없다는 점을 명심해야 합니다. 따라서 경계가 있는 헤세 행렬은 이러한 유형의 문제에만 유용합니다.

다른 작업과의 관계

마지막으로 헤세 행렬은 주로 야코비안 행렬과 라플라스 연산자를 사용하여 다른 중요한 연산이나 행렬과도 연결됩니다.

야코비 행렬과의 관계

함수의 헤세 행렬

$f$

는 동일한 함수의 기울기에 대한 야코비 행렬 입니다.

$\displaystyle H_f = J(\nabla f)$

라플라스 연산자

헤세 행렬 추적은 Laplace 연산자 와 동일합니다.

$\displaystyle tr( H_f) = \Delta f$

라플라스 연산자의 정의는 함수 기울기의 발산이므로 이 동등성은 쉽게 입증될 수 있습니다.

$\displaystyle \Delta f =\nabla \cdot (\nabla f) = (\nabla \cdot \nabla )f = \nabla^2 f$

따라서 그 표현은 다음과 같습니다:

$\displaystyle \Delta f = \cfrac{\partial ^2 f}{\partial^2 x_1} +\cfrac{\partial ^2 f}{\partial^2 x_2} + \cfrac{\partial ^2 f}{\partial^2 x_3}+ \ldots +\cfrac{\partial ^2 f}{\partial^2 x_n}$

그리고 이 합은 헤세 행렬의 자취일 뿐이므로 등가성이 입증됩니다.

헤세 행렬이란 무엇입니까?

헤세 행렬 계산의 예

헤세 행렬의 문제 해결

연습 1

연습 2

연습 3

연습 4

헤세 행렬이 양수, 음수 또는 부정수인지 어떻게 알 수 있나요?

고유값(또는 고유값)의 기준

실베스터 기준

헤세 행렬을 사용하여 함수의 최대값 또는 최소값을 계산하는 방법

다변수 함수의 최대값과 최소값 계산 예

헤세 행렬을 사용하여 함수의 오목성 또는 볼록성 결정

헤세 행렬의 더 많은 응용

테일러 다항식

경계가 있는 삼베 매트릭스

다른 작업과의 관계

야코비 행렬과의 관계

라플라스 연산자

댓글 달기 댓글 취소