이 페이지에서는 무능 행렬이 무엇인지에 대한 설명과 몇 가지 예를 찾아 이해할 수 있으며 의심의 여지가 없습니다. 또한, 무능한 행렬의 구조와 이러한 유형의 행렬의 모든 속성을 볼 수 있습니다.
무능한 행렬이란 무엇입니까?
nilpotent 행렬의 정의는 다음과 같습니다.
무능 행렬(nilpotent 행렬) 은 정수로 올려진 정사각 행렬로 영 행렬을 제공합니다.
![]()
금
![]()
무능한 행렬이고
![]()
제로 행렬을 제공하는 거듭제곱의 지수입니다.
이 조건은 nilpotent 행렬의 거듭제곱이 지수에 관계없이 항상 0을 제공한다는 의미가 아니라 오히려 결과가 0으로 가득 찬 행렬인 행렬의 거듭제곱이 하나 이상 존재하는 경우 해당 행렬은 nilpotent임을 의미합니다.
한편, nilpotency 행렬의 nilpotency index는 nilpotency 조건을 만족하는 가장 작은 숫자입니다. 또한 nilpotent 행렬은 k 차수라고 말할 수 있습니다. 여기서 k 는 nilpotency 지수입니다.
무능한 행렬의 예
무능 행렬의 개념을 완전히 이해하기 위해 이러한 유형의 행렬에 대한 몇 가지 예를 살펴보겠습니다.
2 × 2 무능 행렬의 예
다음과 같은 2×2 차원의 정사각 행렬은 무효입니다.
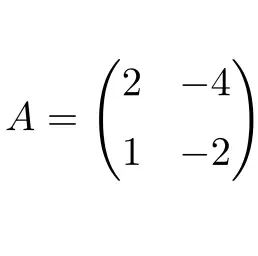
행렬 A를 제곱하여 결과적으로 영 행렬을 얻기 때문에 행렬은 무능합니다.
![Rendered by QuickLaTeX.com \displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fde370dd31b0e2a533fdf1e9d23cf2c9_l3.png)
따라서 영 행렬은 2승으로 얻어지기 때문에 무능 행렬이고 무능 지수는 2입니다.
3×3 무능 행렬의 예
다음 3차 정사각 행렬 은 무효입니다.
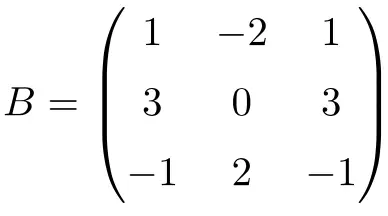
행렬을 2로 올리면 제로 행렬을 얻지 못합니다.
![Rendered by QuickLaTeX.com \displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fbad4ccc270e2960ae50cc23eacc7530_l3.png)
그러나 행렬의 세제곱을 계산할 때 모든 요소가 0인 행렬을 얻습니다.
![Rendered by QuickLaTeX.com \displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-da876a04b14d80c156e24c95bd22372e_l3.png)
따라서 행렬 B는 nilpotent 행렬이고, 영행렬은 3의 거듭제곱을 얻으므로 nilpotency index는 3이다.
2 × 2 무능 행렬의 구조
아래에서는 모든 무능한 행렬의 구조를 볼 수 있습니다. 그 증명은 약간 지루하므로 우리는 2차의 무능한 행렬을 얻기 위한 공식을 직접 제공했습니다:
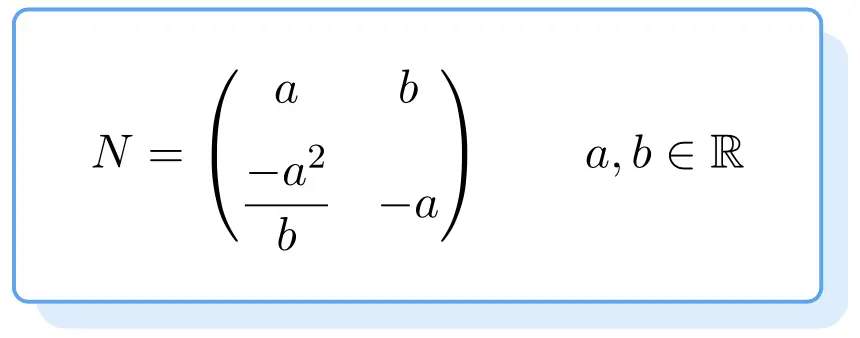
따라서 위 공식을 만족하는 모든 행렬은 무능한 행렬이 됩니다. 이를 위해 가치
![]()
그리고
![]()
실수인 한 임의적일 수 있습니다.
무능한 행렬의 특성
Nilpotent 행렬은 다음과 같은 특성을 갖습니다.
- 무능한 행렬의 흔적은 항상 0입니다.
- 마찬가지로, 모든 무능한 행렬의 행렬식은 항상 0입니다. 그러나 그 반대는 참이 아닙니다. 즉, 행렬의 행렬식이 0이라고 해서 행렬이 무능하다는 것을 의미하지는 않습니다.
- 대각화할 수 있는 유일한 무능 행렬은 영행렬입니다.
- n×n 차원의 무능 행렬의 무능 지수는 항상 n 보다 작거나 같습니다. 이것이 2 × 2 nilpotent 행렬의 nilpotency index가 항상 2인 이유입니다.
- 무능한 행렬은 가역적이지 않습니다.
- 주대각선에 0이 있는 삼각 행렬 도 무능 행렬입니다.
- 행렬이 다음과 같은 정리가 있습니다.

nilpotent이면 행렬은
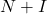
반전 가능합니다. 여기서
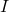
단위 행렬입니다. 또한 역행렬은 다음 공식을 사용하여 찾을 수 있습니다.
![]()
- 마찬가지로, 만약

가 무능한 행렬인 경우 행렬의 역행렬을 계산할 수 있습니다.
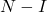
다음 방정식을 사용합니다.
![]()
- 역행렬이 아닌 모든 특이 행렬은 무능 행렬의 곱으로 분해될 수 있습니다.
- nilpotent 행렬의 모든 고유값(또는 고유값)은 0입니다.
![]()
- 마지막으로, 호기심으로 선형 적용을 정의하는 무능 변환(nilpotent Transformation) 개념도 있습니다.
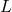
벡터 공간의
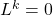
.