이 섹션에서는 행렬식의 모든 속성이 무엇인지 살펴보겠습니다. 또한 예를 들어 각 속성을 완벽하게 이해할 수 있도록 보여줍니다. 또한, 한정사의 속성과 관련된 연습문제도 찾아볼 수 있습니다.
아래에서는 행렬식의 각 속성을 하나씩 설명하겠습니다. 원하는 경우 아래 요약 표로 바로 건너뛸 수 있습니다. 😉
속성 1: 전치 행렬의 행렬식
행렬의 행렬식은 전치된 행렬의 행렬식과 동일합니다.
![]()
예:
![Rendered by QuickLaTeX.com \lvert A \rvert = \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot 3 = 10 - 3 = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7e39b73d52e436c660c2c9f2eeed39f6_l3.png)
이제 2×2 행렬을 전치하고 행렬식을 구합니다. 이전과 동일한 결과를 얻습니다.
![Rendered by QuickLaTeX.com \lvert A^t \rvert = \begin{vmatrix} 2 & 1 \\[1.1ex] 3 & 5 \end{vmatrix} = 2 \cdot 5 - 3 \cdot 1 = 10 - 3 = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc16abe425fb139cb3a6b7ba7e3b1915_l3.png)
속성 2: 행이나 열이 0으로 채워진 행렬식
행렬식에 0으로 채워진 행이나 열이 있는 경우 행렬식은 0을 반환합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a_{11} & 0 & a_{13} \\[1.1ex] a_{21} & 0 & a_{23} \\[1.1ex] a_{31} & 0 & a_{33}\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-54df933d2167697d926c25dd9554d90a_l3.png)
예:
![Rendered by QuickLaTeX.com \begin{vmatrix} 5 & 6 & 2 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] -3 & 1 & 4 \end{vmatrix} = \bm{0} \qquad \qquad \begin{vmatrix} 1 & -5 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 1 & 3 & 0 \end{vmatrix} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-95bc2d762871764f41176acc052a633c_l3.png)
이 두 예제 모두에서 행렬식은 0으로 평가됩니다. 왜냐하면 첫 번째 행렬식의 두 번째 행은 모두 0이고 두 번째 행렬식의 세 번째 열도 모두 0이기 때문입니다.
속성 3: 두 개의 동일한 행 또는 열을 갖는 행렬식
행렬식에 두 개의 동일하거나 여러 행 또는 두 개의 열이 있는 경우 행렬식은 0입니다.
따라서 행이나 열 사이에 선형 결합이 있는 경우, 즉 선형 종속인 경우 행렬식은 0을 제공합니다.
예:
![Rendered by QuickLaTeX.com \begin{vmatrix} 3 & 4 & 4 \\[1.1ex] -1 & 5 & 5 \\[1.1ex] 6 & 2 & 2 \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-c31b59570d4f89e8c7e7aa9f922977c5_l3.png)
이 경우 열 2와 3이 동일하므로 행렬식은 0을 제공합니다.
속성 4: 행렬식의 행 또는 열 수정
두 개의 행이나 두 개의 열이 서로 상대적으로 수정되면 행렬식은 동일한 결과를 제공하지만 부호는 다릅니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{vmatrix}= - \begin{vmatrix} a & c & b \\[1.1ex] d & f & e \\[1.1ex] g & i & h \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-de79fc53e94c9a30d8a271d42d4e3494_l3.png)
예:
![Rendered by QuickLaTeX.com \begin{vmatrix} 3 & 2 & -4 \\[1.1ex] 1 & 5 & 6 \\[1.1ex] 1 & 0 & -3 \end{vmatrix} = \displaystyle -45 +12+0+20-0+6= \bm{-7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2e4806318fa67998b339383a9dc9ea5_l3.png)
이제 열 2와 3의 순서를 서로 상대적으로 변경합니다. 결과는 동일하지만 부호가 다릅니다.
![Rendered by QuickLaTeX.com \begin{vmatrix} 3 & -4 & 2 \\[1.1ex] 1 & 6 & 5 \\[1.1ex] 1 & -3 & 0 \end{vmatrix} = \displaystyle 0-20-6-12+45-0= \bm{+7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4a4de8b8cf37df2c3cce69d16a19a578_l3.png)
속성 5: 행렬식의 행에 스칼라를 곱합니다.
전체 행이나 열의 모든 요소에 실수를 곱하는 것은 행렬식의 결과에 해당 숫자를 곱하는 것과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} k \cdot a_{11} & k \cdot a_{12} & k \cdot a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-06cf5f62a3d703b43bb68b319839df26_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} k \cdot a_{11} & a_{12} & a_{13} \\[1.1ex] k \cdot a_{21} & a_{22} & a_{23} \\[1.1ex] k \cdot a_{31} & a_{32} & a_{33} \end{vmatrix} =k \cdot \begin{vmatrix} a_{11} & a_{12} & a_{13} \\[1.1ex] a_{21} & a_{22} & a_{23} \\[1.1ex] a_{31} & a_{32} & a_{33} \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7b38fe06dab0bbdbfef384b3e403fed_l3.png)
예:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 3 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-3= \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92b404bb7ad8bbdd59c8c54c1619c37d_l3.png)
이제 동일한 행렬식을 사용하여 전체 라인에 2를 곱합니다. 결과는 이전 행렬식의 결과이지만 2 또는 10을 곱한 결과임을 알 수 있습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 \cdot 2 & 2 \cdot 3 \\[1.1ex] 1 & 4 \end{vmatrix} = \begin{vmatrix} 4 & 6 \\[1.1ex] 1 & 4 \end{vmatrix} = 16-6 =\bm{10}](https://mathority.org/wp-content/ql-cache/quicklatex.com-57ae1ba33c0d108f08ac9d0b5cb4a81b_l3.png)
속성 6: 매트릭스 곱의 행렬식
두 행렬의 곱의 행렬식은 각 행렬의 행렬식의 곱과 같습니다.
![]()
예:
행렬식의 이러한 속성을 입증하기 위해 다음 두 행렬의 곱셈의 행렬식을 두 가지 가능한 방법으로 계산합니다.
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix}\quad B=\begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-38de0ca99ad15f40bd94f653cffacf8d_l3.png)
먼저 두 행렬을 곱한 다음 결과 행렬의 행렬식을 계산합니다.
![Rendered by QuickLaTeX.com \displaystyle \left| A \cdot B \right| =\left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = \left| \begin{pmatrix} 7 & -1 \\[1.1ex] 13 & -1 \end{pmatrix} \right| = -7 - (-13) = \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2ad18d1637b581038b7866030d6ac9a0_l3.png)
이제 각 행렬의 행렬식을 개별적으로 계산한 다음 결과를 곱합니다.
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert \cdot \lvert B \rvert = \left| \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 5 \end{pmatrix} \right| \cdot \left| \begin{pmatrix} 4 & 2 \\[1.1ex] 1 & -1 \end{pmatrix}\right| = -1\cdot (-6)= \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5f7c97d5a832d3985bf1d5e9d4d44401_l3.png)
보시다시피, 행렬 곱을 먼저 수행한 다음 행렬식을 수행하면 각 행렬의 행렬식을 먼저 수행한 다음 결과를 곱하는 것과 동일한 결과를 얻을 수 있습니다.
반면에 이 조건은 덧셈과 뺄셈 연산에는 적용되지 않습니다. 즉, 두 행렬의 덧셈(또는 뺄셈)의 행렬식은 다음 행렬식의 덧셈(또는 뺄셈)과 동일한 결과를 제공하지 않습니다. 두 개의 행렬을 별도로 사용합니다.
속성 7: 역행렬의 행렬식
행렬이 역행렬인 경우 역행렬의 행렬식은 원래 행렬의 행렬식의 역행렬에 해당합니다.
![]()
예:
먼저 행렬의 역행렬을 계산한 다음 행렬식을 풀어 이 속성을 검증하겠습니다. 우리는 그 결과가 원래 행렬의 행렬식을 찾아 이를 반전시키는 것과 동일하다는 것을 알게 될 것입니다.
따라서 우리는 다음 행렬을 반전시키고 행렬식을 계산합니다.
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c77c10006d35ebc5273553fb84356e3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A^{-1}= \begin{pmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a9315a8add365cd5f077c52476a827d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A^{-1} \end{vmatrix}= \begin{vmatrix} 2 & -1 \\[1.1ex] -\frac{7}{2} & 2 \end{vmatrix} = 4-\cfrac{7}{2} =\cfrac{8}{2}-\cfrac{7}{2} = \cfrac{\bm{1}}{\bm{2}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a10c873ff6c101cd2b239388393c268b_l3.png)
이제 원래 행렬의 행렬식을 풀고 역행렬을 수행합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}= \begin{pmatrix} 4 & 2 \\[1.1ex] 7 & 4 \end{pmatrix}=16-14=2](https://mathority.org/wp-content/ql-cache/quicklatex.com-850e5404f5352782327918caab3e1440_l3.png)
![]()
보시다시피 두 작업의 결과는 동일합니다. 따라서 해당 속성이 입증되었습니다.
속성 8: 한정자의 행 바꾸기
행렬식의 행은 동일한 행에 다른 행을 더하거나 빼서 숫자를 곱하여 대체할 수 있습니다.
예:
다음 예를 통해 이 속성을 확인하겠습니다. 먼저 행렬식을 계산한 다음 행렬식의 행에 대해 연산을 수행하고 그 결과를 다시 계산합니다. 두 경우 모두에서 동일한 결과를 얻는 방법을 살펴보겠습니다.
따라서 먼저 Sarrus의 규칙을 사용하여 3×3 행렬식을 계산해 보겠습니다.
![Rendered by QuickLaTeX.com \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \displaystyle=0+0+9-0+6-18 = \bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4ccd76fc3a2b7cd7afc7d8f9de8ffde1_l3.png)
이제 두 번째 줄에 2를 곱한 첫 번째 줄을 추가합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 3 & 0 & 1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} \begin{matrix} \\[1.1ex] \xrightarrow{f_2 + 2f_1} \\[1.1ex] \ \end{matrix} \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4bc2e6bd78446fb68f29b4a5503a6828_l3.png)
그리고 우리는 그 직선 중 하나를 변환한 후 행렬식을 푼다:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 & -1 \\[1.1ex] 7 & 2 & -1 \\[1.1ex] 0 & -3 & 6 \end{vmatrix} = 24+0+21-0-6-42=\bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-045eb6f32420fbbf538a9e0a540ce119_l3.png)
두 경우 모두 결과는 -3이었습니다. 따라서 한 행을 같은 행과 다른 행의 합에 숫자를 곱한 값으로 대체해도 행렬식의 결과는 변하지 않음을 알 수 있습니다.
속성 9: 삼각행렬의 행렬식
삼각 행렬의 행렬식은 주대각선 요소의 곱입니다.
예:
예를 들어 다음 삼각 행렬의 행렬식을 풀어 보겠습니다.
![Rendered by QuickLaTeX.com \begin{vmatrix} 2 & 3 & 5 \\[1.1ex] 0 & -1 & 7 \\[1.1ex] 0 & 0 & 4 \end{vmatrix} \displaystyle= 2 \cdot (-1) \cdot 4 = \bm{-8}](https://mathority.org/wp-content/ql-cache/quicklatex.com-40ebfa5f9f06e63ad1325d9331a57bde_l3.png)
속성 10: 대각 행렬의 행렬식
대각 행렬의 행렬식은 주 대각선 요소의 곱셈과 같습니다.
예:
다음 대각 행렬의 행렬식을 예로 들어 보겠습니다.
![Rendered by QuickLaTeX.com \begin{vmatrix}5 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -2 \end{vmatrix} \displaystyle= 5 \cdot 3 \cdot (-2) = \bm{-30}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56e1b3093685a1af729310752b03dfc9_l3.png)
행렬식의 속성 요약표
설명된 행렬식의 속성은 다음 표에 요약되어 있습니다.
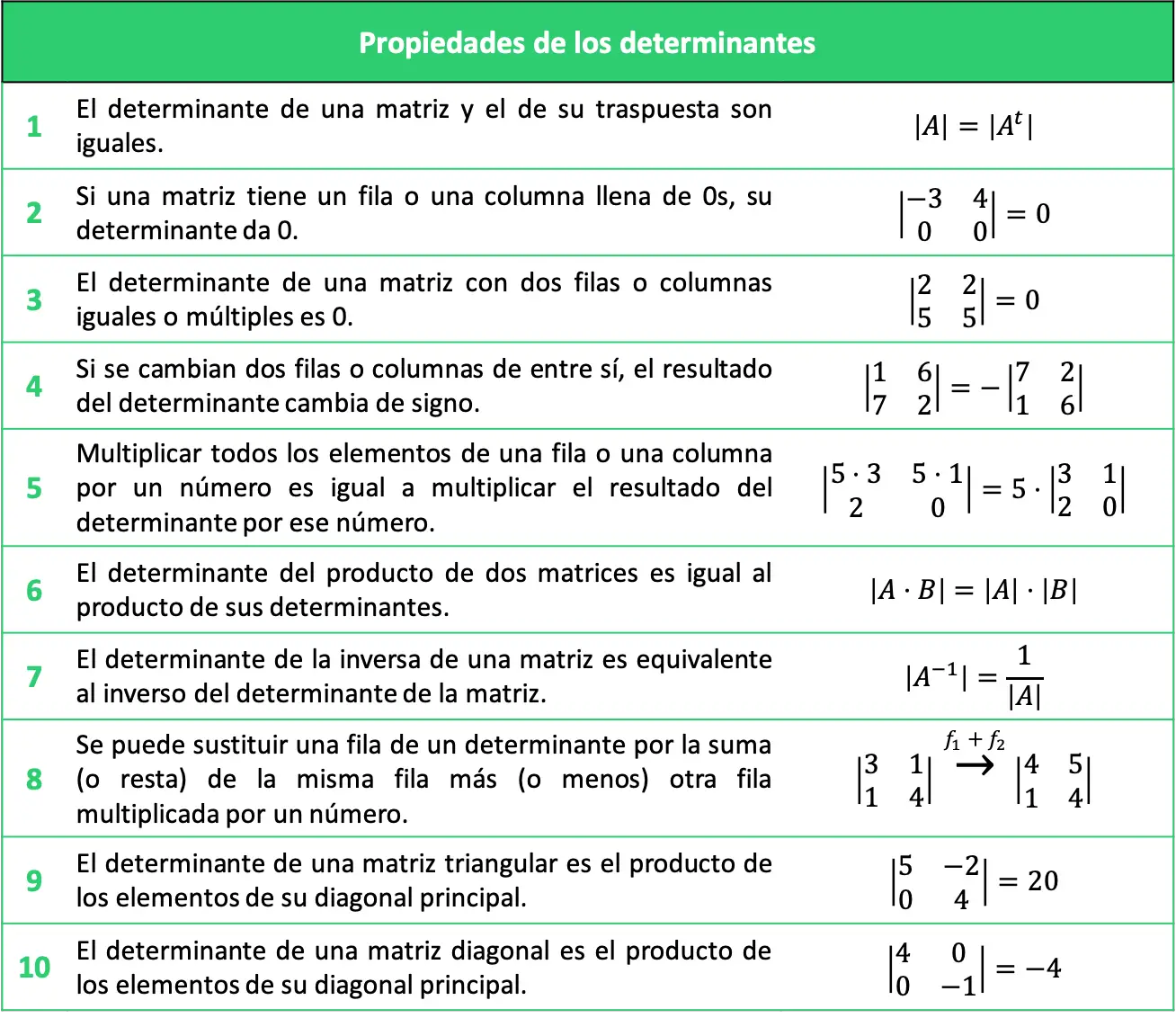
행렬식의 속성을 이용한 연습문제 해결
연습 1
다음 행렬식을 푼다:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3 & 1 & 0 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -1 & 6 & 0 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-97dfc1ebfc5db73750870911108bd447_l3.png)
행렬식에 0으로 채워진 행이나 열이 있는 경우 행렬식은 0(속성 2)을 반환합니다. 따라서 세 번째 열이 0으로 채워지기 때문에 행렬식의 결과는 0입니다.
연습 2
다음 행렬식을 푼다:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 4 & 2 & -3 & 5 \\[1.1ex] 1 & 5 & 3 & 2 \\[1.1ex]4 & 2 & -3 & 5 \\[1.1ex] -2 & 0 & 4 & 3 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bdb315ba588fe5fdfb03c7fea2857b16_l3.png)
행렬식에 두 개의 동일하거나 여러 행 또는 두 개의 열이 있는 경우 행렬식은 0(속성 3)을 반환합니다. 따라서 첫 번째 행과 세 번째 행이 동일하므로 행렬식의 결과는 0입니다.
연습 3
다음 행렬식을 계산합니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 0 & 2 & 2 \\[1.1ex] 3 & 1 & 5 & 6 \\[1.1ex] 1 & 3 & -2 & 2 \\[1.1ex] 2 & 2 & 0 & 4 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96c5cfee4c4189e49b54fdf43b2a0457_l3.png)
행렬식에 두 개의 동일하거나 여러 행 또는 두 개의 열이 있는 경우 행렬식은 0(속성 3)을 반환합니다. 따라서 네 번째 열이 첫 번째 열의 두 배이므로 행렬식의 결과는 0입니다.
연습 4
행렬의 요소는 모르지만 행렬식의 결과는 알고 있습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-e20d9016edd52f18d3ffc928d2658efe_l3.png)
이전 행렬식의 결과와 행렬식의 속성으로부터 다음 행렬식의 결과를 계산합니다.
![Rendered by QuickLaTeX.com \displaystyle \mathbf{a} \bm{)} \ \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix} \qquad \mathbf{b} \bm{)} \ \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} \qquad \mathbf{c} \bm{)} \ \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9c20de8d82171dc8fb784e2549521f37_l3.png)
을 위한)
![]()
은 전치된 행렬이다
![]()
. 그리고 행렬의 행렬식은 전치된 행렬의 행렬식과 같습니다(속성 1). 따라서 이 행렬식의 결과도 3입니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & c \\[1.1ex] b & d \end{vmatrix}=\begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}=\bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5bf7ae0a2ff32d75a6f7abafb623639c_l3.png)
b) 결정에서
![]()
열 1과 2는 명령문의 결정자와 관련하여 수정되었습니다.
![]()
. 따라서 속성 4에 따르면 결과는 명령문의 한정사의 결과와 동일하지만 부호가 다릅니다(예: -3).
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} b & a \\[1.1ex] d & c \end{vmatrix} = - \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix}= \bm{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6d14aa2f6b8c7d1fd064daef8dd0eec_l3.png)
c) 결정에서
![]()
명령문 행렬식의 전체 두 번째 열에 3을 곱했습니다. 따라서 속성 5에서 해당 결과가 명령문 행렬식에 3을 곱한 결과, 즉 9가 될 것임을 추론할 수 있습니다.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} a & 3b \\[1.1ex] c & 3d \end{vmatrix} =3 \begin{vmatrix} a & b \\[1.1ex] c & d \end{vmatrix} =3 \cdot 3 = \bm{9}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1a7ffec429367a2fd967a197d0299d2_l3.png)
연습 5
우리는 이 두 가지 행렬식의 결과를 알고 있습니다.
![Rendered by QuickLaTeX.com \displaystyle\vert A \vert = \begin{vmatrix} 1 & 2 & 0 & 1 \\[1.1ex] -2 & -1 & 1 & 0 \\[1.1ex] 1 & 3 & 3 & -1 \\[1.1ex] 3 & 4 & 1 & 1 \end{vmatrix}=8](https://mathority.org/wp-content/ql-cache/quicklatex.com-e938c40ce401263da9835fa77fc9a1dd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\vert B \vert = \begin{vmatrix} 0 & 1 & 3 & 2 \\[1.1ex] -1 & -2 & 0 & 0 \\[1.1ex] 3 & 1 & 1 & 2 \\[1.1ex] -1 & 2 & 3 & 1 \end{vmatrix} = - 4](https://mathority.org/wp-content/ql-cache/quicklatex.com-6cea0d73e66099f2a10f71f7267baee9_l3.png)
이 정보를 바탕으로 다음을 계산합니다.
![]()
행렬식의 결과를 계산하기 위해 4×4 행렬을 곱할 필요는 없습니다. 두 행렬의 곱의 행렬식은 각 행렬의 행렬식의 곱과 같기 때문입니다 (속성 6). 아직:
![]()