Antihermitian(또는 antihermitian) 행렬

이 페이지에서는 항에르미트 행렬(antihermitian Matrix)이라고도 불리는 항에르미트 행렬(antihermitian Matrix)이 무엇인지 살펴보겠습니다. 반 에르미트 행렬(anti-Hermitian matrices)의 예, 모든 속성 및 이러한 유형의 복소 정사각형 행렬의 모양을 찾을 수 있습니다. 마지막으로 복잡한 행렬을 반 에르미트 행렬과 또 다른 에르미트 행렬의 합으로 분해하는 방법에 대한 설명을 찾을 수 있습니다.

항에르미트 행렬 또는 항에르미트 행렬이란 무엇입니까?

반 에르미트 행렬(Anti-Hermitian Matrix) 또는 반 에르미트 행렬(Anti-Hermitian Matrix)이라고도 불리는 것은 켤레 전치가 동일한 행렬과 같지만 부호가 다른 복소수를 갖는 정사각 행렬입니다.

$A^*=-A$

금

$A^*$

는 전치된 켤레 행렬 입니다.

$A$

호기심에서 이런 유형의 행렬은 에르미트 행렬(Hermitian Matrix) 의 반대 조건을 충족하기 때문에 그렇게 불립니다. 이 행렬의 이름은 프랑스의 중요한 수학자 샤를 에르미트(Charles Hermite)에서 유래되었습니다. 샤를 에르미트는 19세기 수학 교수이자 연구원으로 다음과 같은 중요한 연구를 했습니다. 선형대수학 분야.

반 에르미트 행렬의 예

AntiHermitian 행렬(또는 AntiHermitian 행렬)의 정의를 확인한 후에는 다양한 차원의 AntiHermitian 행렬의 몇 가지 예를 볼 수 있습니다.

2×2 차수 반 에르미트 행렬의 예

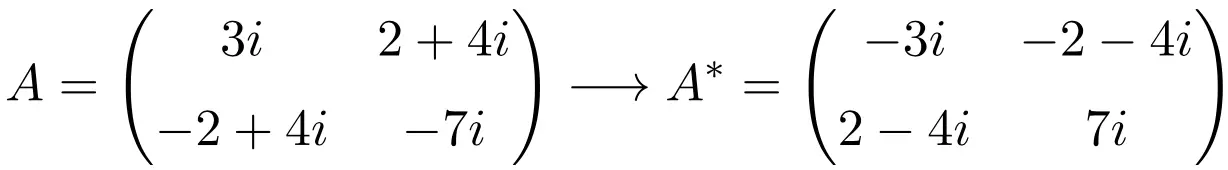
차원 3×3의 반에르미트 행렬의 예

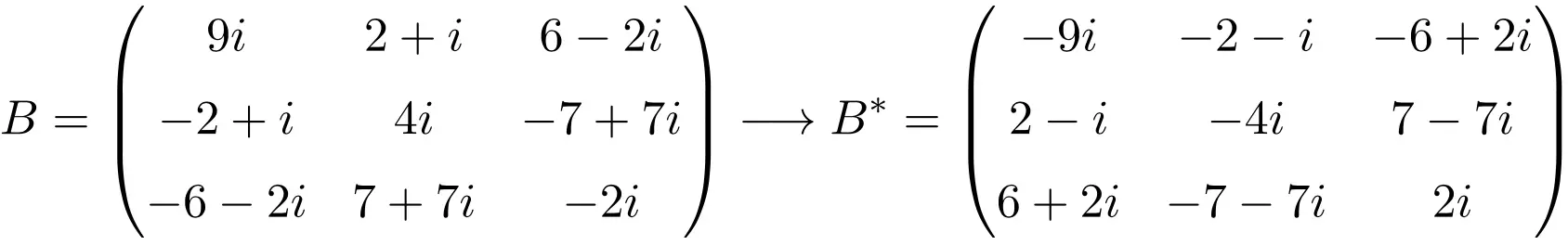
크기가 4×4인 반 에르미트 행렬의 예

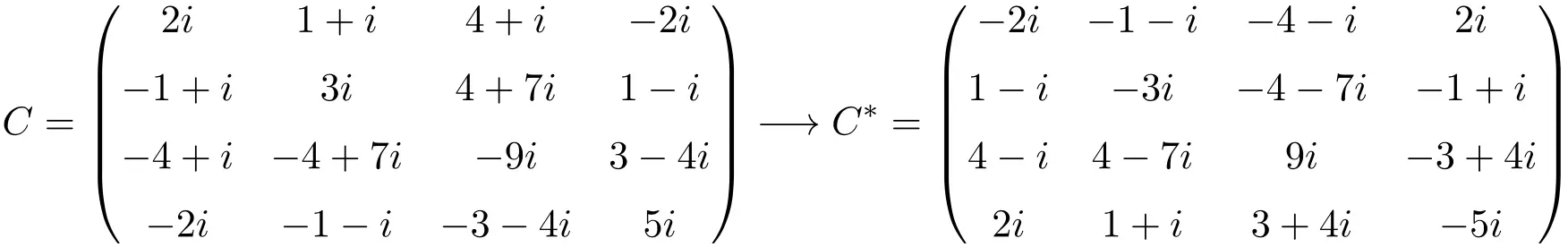
보시다시피, 행렬 A, B, C는 각각의 켤레 전치 행렬이 행렬 자체와 동일하지만 모든 요소의 부호가 변경되었기 때문에 반 에르미트 행렬입니다.

항헤르미트 행렬의 구조

이전 예제를 이미 살펴보았다면 반 에르미트 행렬은 항상 동일한 구조를 갖습니다. 주대각선의 허수(실수 부분 없음)와 i번째 행과 j번째 행에 위치한 복소수 요소로 구성됩니다. 선. 열은 허수부와 실수부가 동일해야 하며 j번째 행과 i번째 열의 요소로 부호가 변경되어야 합니다.

다소 복잡해 보일 수도 있지만 다음 예를 보면 확실히 더 잘 이해할 수 있습니다.

차원 2×2의 반에르미트 행렬의 구조

$\displaystyle \begin{pmatrix} ai & b+ci\\[1.1ex]-b+ci & di \end{pmatrix}$

보시다시피, 반 에르미트 행렬의 주대각선 요소는 완전히 허수이고 두 번째 대각선의 요소는 동일한 허수 부분을 가지며 실수 부분의 부호가 변경되었습니다.

따라서 반 에르미트 행렬의 실수 부분은 반대칭이어야 하고 허수 부분은 대칭이어야 합니다.

항헤르미트 매트릭스의 특성

이제 이러한 유형의 정사각 복소 행렬의 속성이 무엇인지 살펴보겠습니다.

각각의 반 에르미트 행렬은 정규 행렬의 예 입니다. 모든 일반 행렬이 항은둔 행렬은 아니지만.

모든 반 에르미트 행렬은 대각선화 가능합니다. 또한 결과 대각 행렬에는 순전히 허수 요소만 포함됩니다.

따라서 반 에르미트 행렬의 고유값(또는 고유값)은 항상 허수입니다.

마찬가지로, 반 에르미트 행렬의 서로 다른 고유값의 고유벡터(또는 고유벡터)는 직교합니다.

실수 행렬, 즉 어떤 요소에도 허수 부분이 없다는 행렬은 반대칭 행렬인 경우에만 반 에르미트 행렬입니다.

반 에르미트 행렬은 실수 반대칭 행렬과 허수 대칭 행렬 의 합으로 표현될 수 있습니다.

$A =B+Ci$

두 개의 반 에르미트 행렬의 합(또는 빼기)은 다른 반 에르미트 행렬과 같습니다.

반 에르미트 행렬과 스칼라를 곱한 결과는 스칼라가 실수인 경우 또 다른 반 에르미트 행렬이 됩니다.

반 에르미트 행렬의 거듭제곱은 지수가 홀수인 경우 반 에르미트 행렬과 동일합니다. 반면, 짝수 지수로 올리면 결과는 에르미트 행렬이 됩니다.

응
$A$

는 항에르미트 행렬(antihermitian Matrix)이고, 그러면 생성물은

$iA$

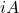
에르미트 행렬이다.

복소 행렬을 반 에르미트 행렬과 에르미트 행렬로 분해

복소수를 포함하는 모든 행렬은 반 에르미트 행렬과 또 다른 에르미트 행렬의 합으로 분해 될 수 있습니다. 그러나 이를 위해서는 이러한 유형의 행렬의 다음 특성을 알아야 합니다.

정사각 복소수 행렬과 전치 공액의 합은 Hermitian(또는 Hermitian) 행렬과 동일합니다.

$C + C^* = \text{Matriz Hermitiana}$

정사각 복소수 행렬과 전치된 공액의 차이는 반 에르미트 행렬과 같습니다.

$C - C^* = \text{Matriz Antihermitiana}$

따라서 모든 복소수 행렬은 에르미트 행렬과 반 에르미트 행렬의 합으로 분해될 수 있습니다. 이 정리는 테오 플리츠 분해(Teoplitz decomposition) 로 알려져 있습니다:

$\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}$

여기서 C는 분해하려는 복소 행렬이고, C*는 전치된 켤레이며, 마지막으로 A와 B는 각각 행렬 C가 분해되는 에르미트 행렬과 반 에르미트 행렬입니다.

항에르미트 행렬 또는 항에르미트 행렬이란 무엇입니까?

반 에르미트 행렬의 예

항헤르미트 행렬의 구조

항헤르미트 매트릭스의 특성

복소 행렬을 반 에르미트 행렬과 에르미트 행렬로 분해

댓글 달기 댓글 취소