기능 표현 -

이 기사에서는 그래프에 모든 유형의 함수를 표현하는 방법을 살펴보겠습니다. 또한 그래프에 함수를 표시하는 방법에 대한 단계별 연습 문제도 찾을 수 있습니다.

그래프에 함수를 표현하는 방법

그래프에 함수를 나타내려면 다음 단계를 수행해야 합니다.

함수의 정의역을 찾으세요.
데카르트 축을 사용하여 함수의 컷오프 지점을 계산합니다.
함수의 점근선을 계산합니다.
함수의 단조성을 연구하고 상대적인 극단을 찾아보세요.
함수의 곡률을 연구하고 변곡점을 찾습니다.
컷오프점, 점근선, 상대 극값 및 변곡점을 플로팅 한 다음 함수를 플로팅합니다.

함수 표현의 예

함수가 그래픽으로 어떻게 표현되는지 확인할 수 있도록 다음 연습 문제를 단계별로 풀어보겠습니다.

다음 유리함수를 그래프에 그려보세요:

$f(x)=\cfrac{x^2}{x-1}$

가장 먼저 해야 할 일은 함수의 정의역을 계산하는 것 입니다. 이것은 유리함수이므로 함수의 정의역에 속하지 않는 숫자를 확인하려면 분모를 0으로 설정해야 합니다.

$x-1=0$

$x=1$

따라서 x가 1이면 분모는 0이 되므로 함수는 존재하지 않습니다. 따라서 함수의 정의역은 x=1을 제외한 모든 실수로 구성됩니다.

$\text{Dom } f= \mathbb{R}-\{1 \}$

X축과의 교차점을 찾으려면 다음 방정식을 풀어야 합니다.

$f(x)= 0.$

함수의 X축 값은 항상 0이므로:

$f(x)=0$

$\cfrac{x^2}{x-1} = 0$

용어

$x -1$

여기에는 전체 왼쪽을 나누는 작업이 포함되므로 전체 오른쪽을 곱할 수 있습니다.

$x^2 = 0 \cdot (x-1)$

$x^2 = 0$

$x = 0$

따라서 OX 축과의 교차점은 다음과 같습니다.

$\bm{(0,0)}$

그리고 Y축과의 교차점을 찾기 위해 다음을 계산합니다.

$f(0).$

x는 Y축에서 항상 0이므로:

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0$

따라서 OY 축의 컷오프 지점은 다음과 같습니다.

$\bm{(0,0)}$

이 경우 함수가 좌표원점을 통과할 때 X축과의 교점은 Y축과의 교점과 일치하게 된다.

정의역과 컷오프 포인트를 알고 나면 함수의 점근선을 계산해야 합니다.

함수에 수직 점근선이 있는지 확인하려면 정의역에 속하지 않는 점(이 경우 x=1)에서 함수의 극한을 계산해야 합니다. 그리고 결과가 무한하다면 수직 점근선이 됩니다. 아직:

$\displaystyle \lim_{x \to 1} \ \cfrac{x^2}{x-1} = \cfrac{1^2}{1-1} = \cfrac{1}{0} = \infty$

x가 1로 경향일 때 함수의 극한은 무한대를 제공하므로 x=1은 수직 점근선입니다:

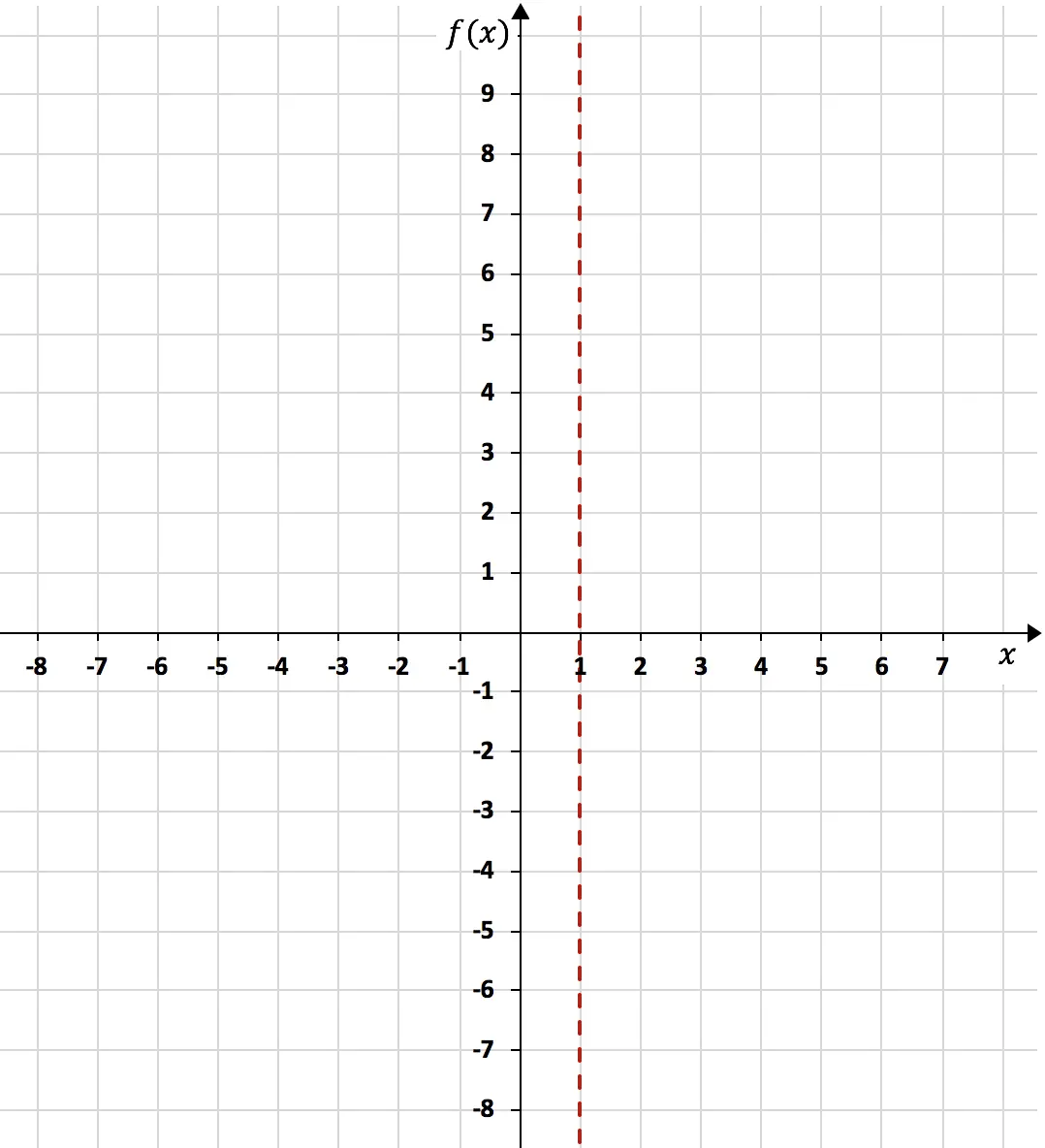
수직 점근선이 계산되면 이에 대한 함수의 측면 한계를 계산해야 합니다. 함수가 왼쪽에서 x=1에 접근할 때 함수가 -무효 또는 +무효로 변하는 경향이 있는지 알 수 없고, 오른쪽에서 x=1에 접근할 때도 알 수 없습니다.

따라서 x=1에서 함수의 왼쪽 측면 극한을 계산합니다.

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1}$

한 점에서 측면 경계를 수치적으로 계산하려면 해당 점에 매우 가까운 함수에 숫자를 대입해야 합니다. 이 경우 왼쪽에 0.9와 같이 1에 매우 가까운 숫자가 필요합니다. 따라서 함수에서 점 0.9를 대체합니다.

$\cfrac{0,9^2}{0,9-1}=\cfrac{0,81}{-0,1}=-81$

점근선에 대한 측면 극한은 +무한대 또는 -무한대만 제공할 수 있습니다. 그리고 왼쪽에 있는 1에 매우 가까운 숫자를 함수에 대입하여 음수 결과를 얻었으므로 왼쪽의 한계는 -무한대입니다.

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1} = \bm{-\infty}$

이제 오른쪽 경계에 대해 동일한 절차를 수행합니다.

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1}$

함수의 오른쪽에 있는 1에 매우 가까운 숫자를 대체합니다. 예를 들어 포인트 1.1은 다음과 같습니다.

$\cfrac{1,1^2}{1,1-1}=\cfrac{1,21}{0,1}=+12,1$

이 경우 측면 제한 결과는 양수입니다. 따라서 우변의 극한은 +입니다:

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1} = \bm{+\infty}$

결론적으로, x=1에서 함수는 왼쪽에서 마이너스 무한대를 향하고 오른쪽에서 플러스 무한대를 향하는 경향이 있습니다.

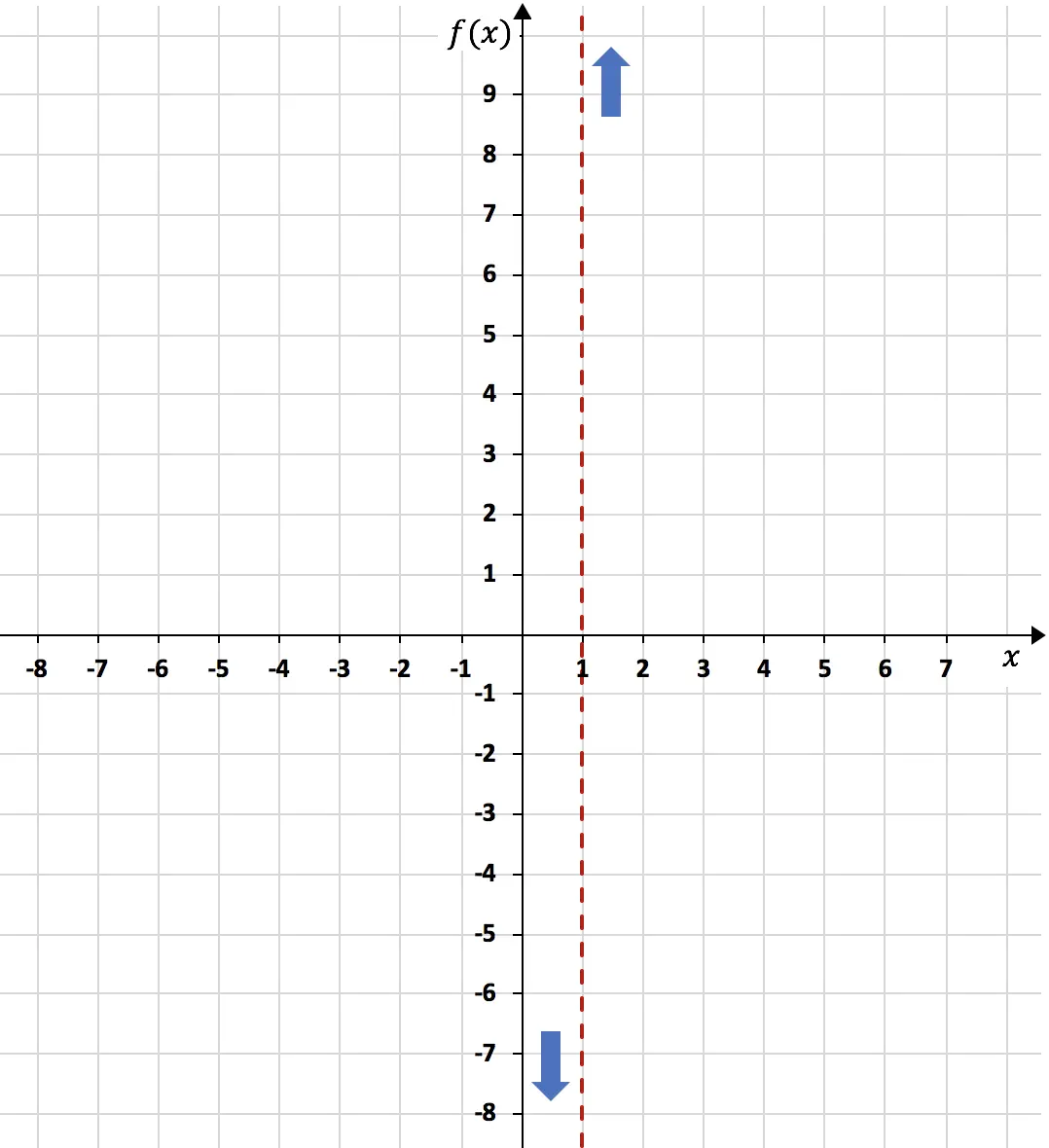
반면에, 함수의 수평 점근선은 함수의 무한 극한의 결과가 될 것입니다. 아직:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2}{x-1} = \cfrac{+\infty}{+\infty } =+\infty$

유리함수의 무한한계를 계산하는 방법을 기억하세요 :

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> </div> 함수의 무한한계는 +무한대를 제공하므로 함수에는 수평 점근선이 없습니다. 이제 경사 점근선을 계산합니다. 경사 점근선의 형식은 다음과 같습니다. <p class=$ $y=mx+n$

. 그리고

$m$

다음 공식으로 계산됩니다.

$\displaystyle m = \lim_{x \to +\infty} f(x):x$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:x$

x는 분모가 1인 것과 같습니다.

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:\cfrac{x}{1}$

이것은 분수의 나눗셈이므로 가로로 곱합니다.

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 \cdot 1 }{(x-1) \cdot x}$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x}$

그리고 우리는 한계를 계산합니다:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x} = \cfrac{+\infty}{+\infty } = \cfrac{1}{1} = 1$

따라서 m=1입니다. 이제 우리는 계산합니다

$n$

다음 공식을 사용합니다.

$\displaystyle n = \lim_{x \to +\infty} \bigl[f(x)-mx\bigr]$

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty$

그러나 우리는 불확정성 무한대 마이너스 무한대를 얻습니다. 따라서 항을 공통 분모로 줄여야 합니다. 이를 위해 항 x를 분수의 분모로 곱하고 나눕니다.

$\displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]$

이제 두 용어의 분모가 동일하므로 그룹화할 수 있습니다.

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]$

그리고 마지막으로 한계를 해결합니다.

$\displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1$

따라서 n = 1입니다. 따라서 경사 점근선은 다음과 같습니다.

$y = mx+n$

$y = 1x+1$

$\bm{y = x+1}$

경사 점근선을 계산한 후에는 값 테이블을 만들어 동일한 그래프에 이를 나타냅니다.

$y=x+1$

$\begin{array}{c|c} x & y \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \end{array}$

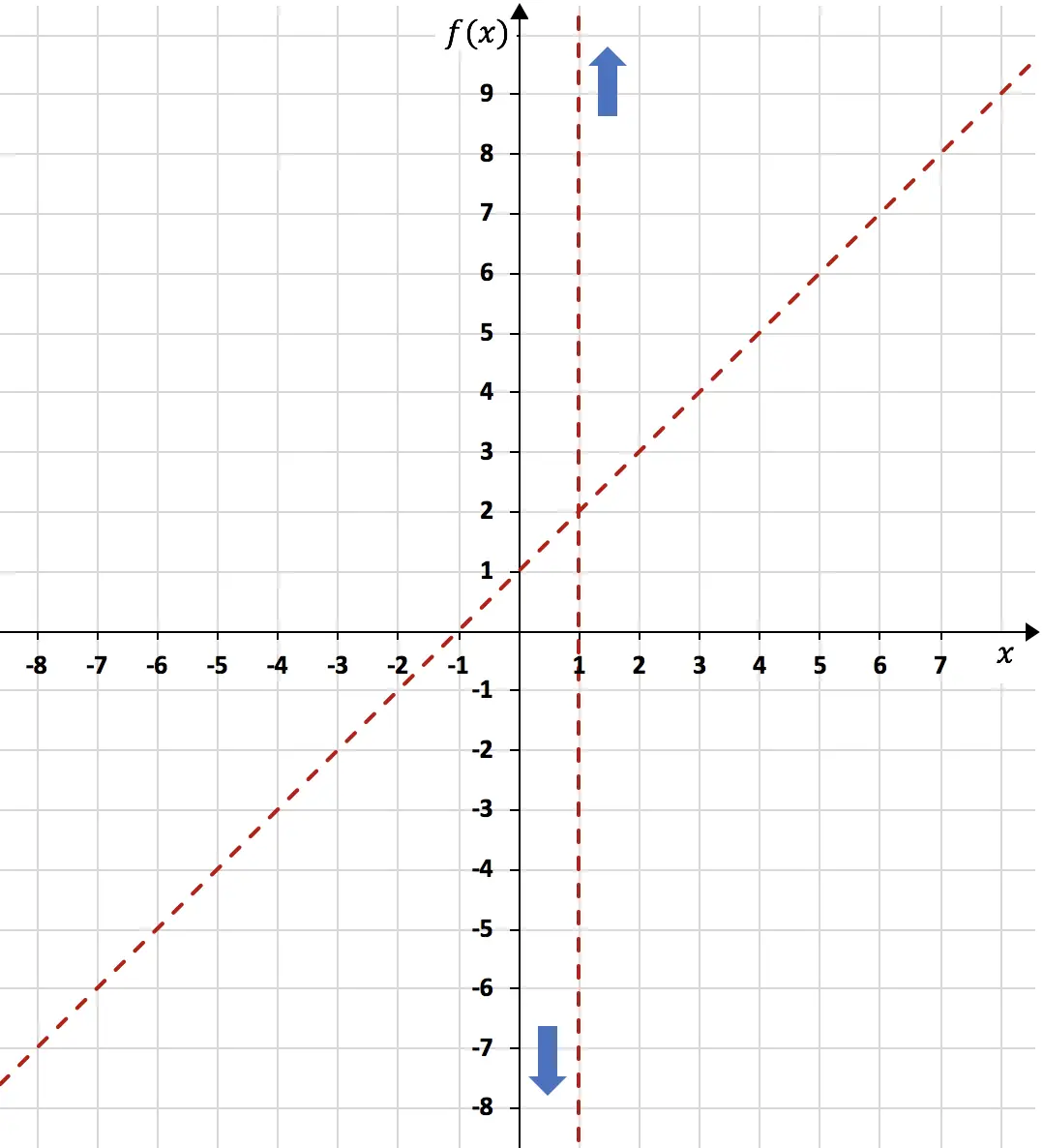
이제 함수의 점근선을 모두 알았으므로 함수의 단조성을 분석해야 합니다. 즉, 어느 구간에서 함수가 증가하고 어느 구간에서 감소하는지 연구해야 합니다. 따라서 우리는 함수의 1차 도함수를 계산합니다.

$f(x)=\cfrac{x^2}{x-1} \ \longrightarrow \ f'(x)= \cfrac{2x\cdot (x-1) - x^2 \cdot 1}{(x-1)^2}$

$f'(x)= \cfrac{2x^2-2x - x^2}{(x-1)^2} = \cfrac{x^2-2x}{(x-1)^2}$

이제 도함수를 0으로 설정하고 방정식을 풉니다.

$f'(x)=0$

$\cfrac{x^2-2x}{(x-1)^2}=0$

용어

$\left(x-1\right)^2}$

여기에는 전체 왼쪽을 나누는 작업이 포함되므로 전체 오른쪽을 곱할 수 있습니다.

$x^2-2x=0\cdot \left(x-1\right)^2$

$x^2-2x=0$

이차방정식을 풀기 위해 공통인수를 추출합니다:

$x(x-2)=0$

곱셈이 0이 되려면 곱셈의 두 요소 중 하나가 0이어야 합니다. 따라서 각 요소를 0으로 설정하고 방정식의 두 해를 모두 얻습니다.

$\displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}$

이제 발견된 모든 임계점, 즉 영역에 속하지 않는 점(x=1)과 도함수를 취소하는 점(x=0 및 x=2)을 수직선에 나타냅니다.

그리고 각 간격에서 도함수의 부호를 평가하여 함수가 증가하는지 감소하는지 확인합니다. 따라서 우리는 각 구간에서 한 점(임계점은 아님)을 취하고 해당 점에서 도함수가 어떤 부호를 갖는지 살펴봅니다.

$f'(x)=\cfrac{x^2-2x}{\left(x-1\right)^2}$

$f'(-1) = \cfrac{(-1)^2-2(-1)}{\left((-1)-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

$f'(0,5) = \cfrac{0,5^2-2\cdot 0,5}{\left(0,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(1,5) = \cfrac{1,5^2-2\cdot 1,5}{\left(1,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(3) = \cfrac{3^2-2\cdot 3}{\left(3-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

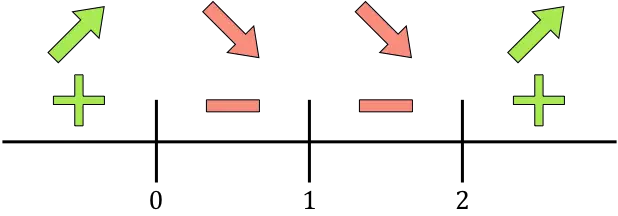
도함수가 양수이면 함수가 증가한다는 의미이고, 도함수가 음수이면 함수가 감소한다는 의미입니다. 따라서 성장 및 쇠퇴 간격은 다음과 같습니다.

성장:

$\bm{(-\infty, 0)\cup (2,+\infty)}$

감소하다:

$\bm{(0,1)\cup (1,2)}$

또한 x=0에서 함수는 증가에서 감소로 이동하므로 x=0은 함수의 상대적 최대값입니다. 그리고 x=2에서 함수는 감소에서 증가로 이동하므로 x=2는 함수의 상대적 최소값입니다.

마지막으로 점의 Y 좌표를 찾기 위해 원래 함수에서 찾은 극단을 대체합니다.

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0 \ \longrightarrow \ (0,0)$

$f(2)=\cfrac{2^2}{2-1} = \cfrac{4}{1} = 4 \ \longrightarrow \ (2,4)$

따라서 함수의 상대적 극단은 다음과 같습니다.

포인트 최대값

$\bm{(0,0)}$

포인트까지의 최소

$\bm{(2,4)}$

그래프에 최대값과 최소값을 나타냅니다.

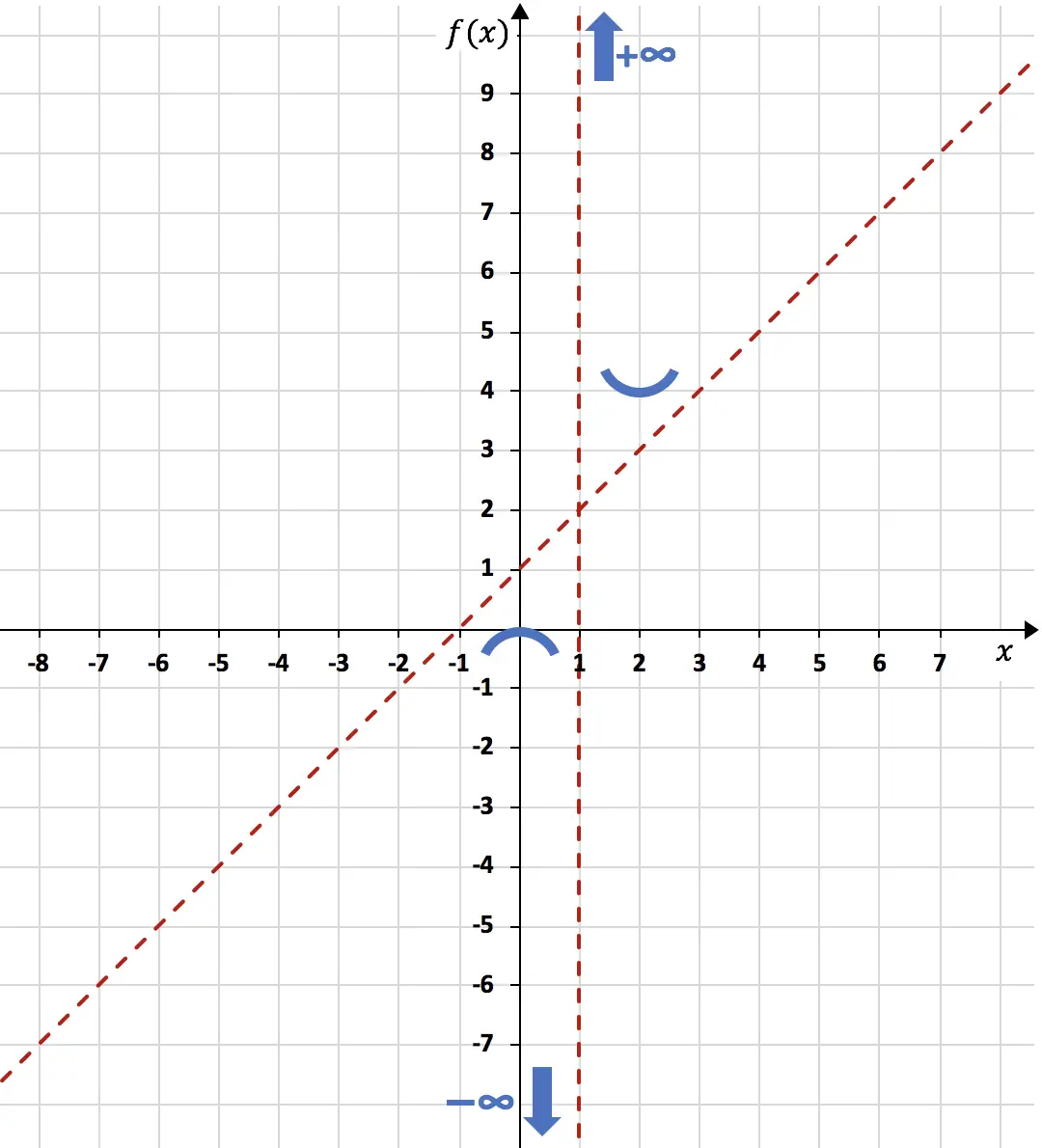
마지막으로 함수의 곡률을 연구하는 것 , 즉 함수의 오목함과 볼록함의 간격을 연구하는 것으로 충분합니다. 이를 위해 2차 미분을 계산합니다.

$f'(x)=\cfrac{x^2-2x}{(x-1)^2} \ \longrightarrow \ f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)\cdot 1}{\left(\left(x-1\right)^2\right)^2}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)}{(x-1)^4}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^{\cancel{2}}- (x^2-2x)\cdot 2\cancel{(x-1)}}{(x-1)^{\cancelto{3}{4}}} = \cfrac{(2x-2)\cdot (x-1)- (x^2-2x)\cdot 2}{(x-1)^3}$

$f''(x)= \cfrac{2x^2-2x-2x+2- (2x^2-4x)}{(x-1)^3} =\cfrac{2x^2-2x-2x+2- 2x^2+4x}{(x-1)^3}$

$f''(x) =\cfrac{2}{(x-1)^3}$

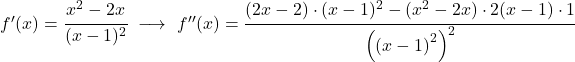
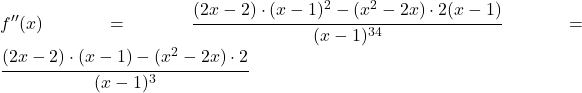
이제 2차 도함수를 0으로 설정하고 방정식을 풉니다.

$f''(x)=0$

$\cfrac{2}{(x-1)^3} =0$

$2=0\cdot \left(x-1\right)^3$

$2=0$

2는 결코 0과 같지 않으므로 방정식은 다음과 같습니다.

$f''(x)=0$

해결책이 없습니다.

이제 발견된 모든 임계점, 즉 도메인에 속하지 않는 점(x=1)과 2차 도함수를 취소하는 점(이 경우에는 포함되지 않은 점)을 수직선에 나타냅니다.

그리고 우리는 함수가 볼록인지 오목인지를 알기 위해 각 구간에서 도함수의 부호를 평가합니다. 따라서 우리는 각 간격에서 점(특이점은 아님)을 취하고 이 점에서 도함수가 어떤 부호를 갖는지 살펴봅니다.

$f''(x) =\cfrac{2}{(x-1)^3}$

$f''(0) =\cfrac{2}{(0-1)^3} = \cfrac{2}{-1}=-2 \ \rightarrow \ \bm{-}$

$f''(2) =\cfrac{2}{(2-1)^3} = \cfrac{2}{1}=2 \ \rightarrow \ \bm{+}$

그리고 마지막으로 함수의 오목함과 볼록함의 간격을 추론합니다. 2차 도함수가 양수이면 함수가 볼록함을 의미합니다.

$(\bm{\cup})$

, 그리고 2차 도함수가 음수이면 이는 함수가 오목함을 의미합니다.

$(\bm{\cap})$

. 따라서 오목 및 볼록 간격은 다음과 같습니다.

볼록한

$(\bm{\cup})$

$\bm{(1,+\infty)}$

오목한

$(\bm{\cap})$

$\bm{(-\infty,1)}$

그러나 x=1에서 곡률의 변화가 있더라도 변곡점은 아닙니다. x=1은 함수의 정의역에 속하지 않기 때문입니다.

이제 우리가 계산한 모든 것을 사용하여 함수 표현을 마칠 수 있습니다.

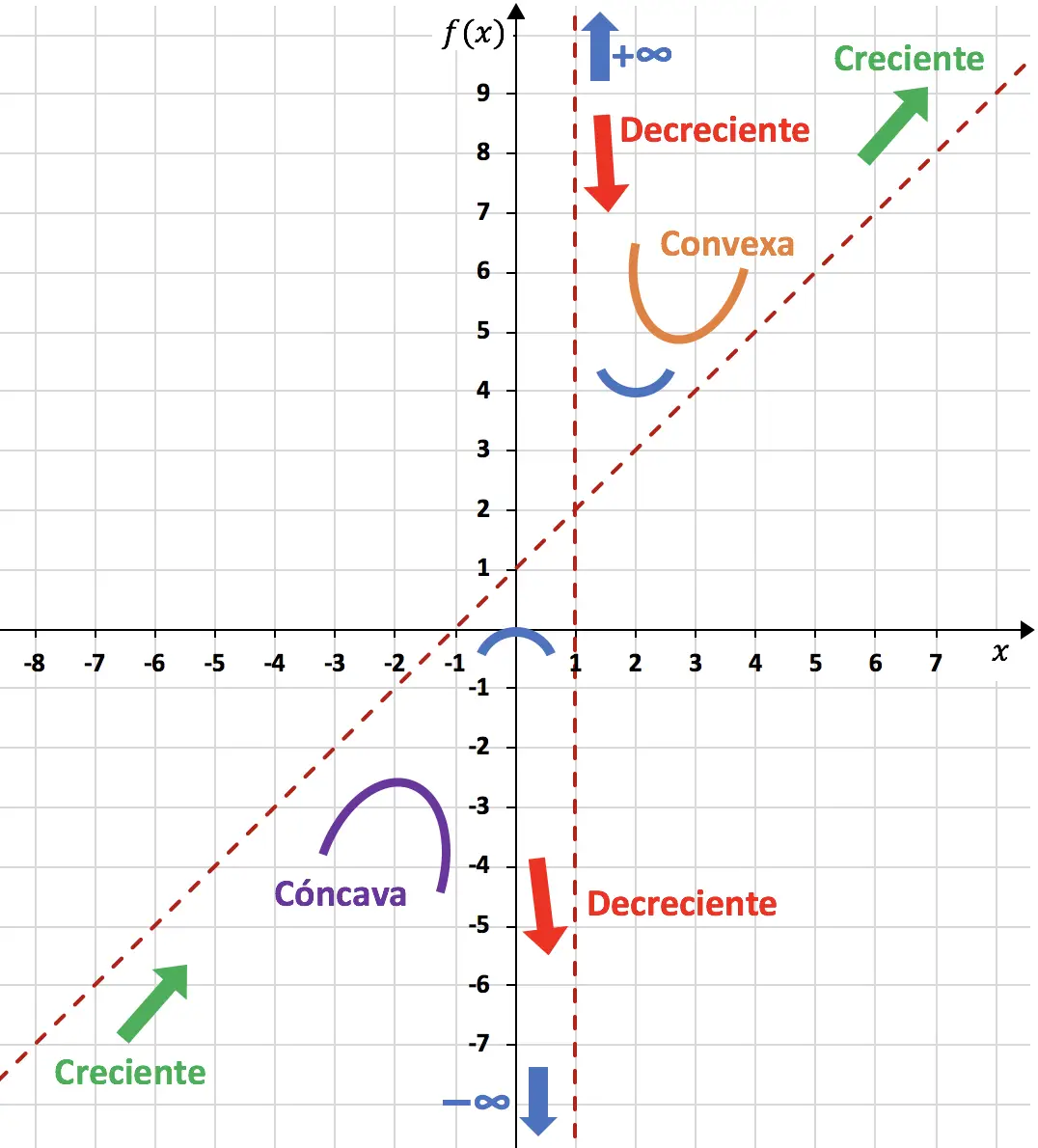
따라서 그래프에 표시된 함수는 다음과 같습니다.

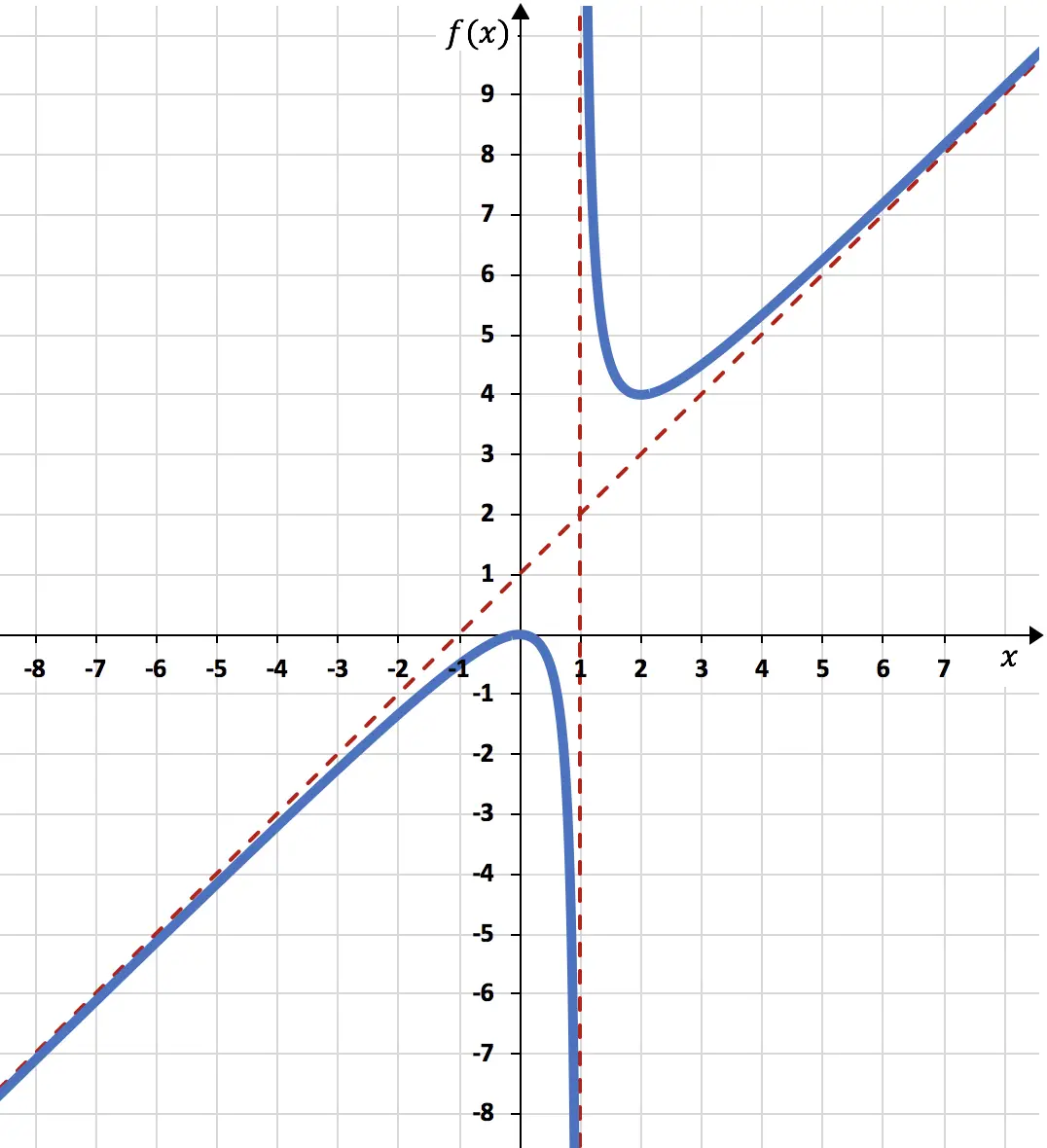
함수를 표현하는 연습문제 해결

연습 1

다음 다항식 함수를 그래프로 나타내십시오.

$\displaystyle f(x)=x^3-3x^2+4$

솔루션 보기

가장 먼저 해야 할 일은 함수의 정의 영역을 계산하는 것입니다. 이것은 다항식 함수이므로 정의역은 실수로만 구성됩니다.

$\text{Dom } f= \mathbb{R}$

X축과의 교차점을 찾기 위해 다음을 해결합니다.

$f(x)= 0.$

$f(x)=0$

$x^3-3x^2+4=0$

이는 2보다 큰 차수 방정식입니다. 따라서 방정식을 고려합니다.

$(x+1)(x^2-4x+4)=0$

따라서 x=-1이 해입니다. 그리고 결과 이차 방정식을 풀어서 다른 해를 계산합니다.

$\begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}$

따라서 X축과의 교차점은 다음과 같습니다.

$\bm{(-1,0)}$

그리고

$\bm{(2,0)}$

그리고 Y축과의 교차점을 찾기 위해 다음을 계산합니다.

$f(0).$

x는 Y축에서 항상 0이므로:

$f(0)=0^3-3\cdot0^2+4 = 4$

따라서 Y축과의 교차점은 다음과 같습니다.

$\bm{(0,4)}$

함수에 수직 점근선이 있는지 확인하려면 도메인에 속하지 않는 점에서 함수의 극한을 계산해야 합니다. 이 경우 정의역에는 모든 실수가 포함됩니다. 따라서 함수에는 수직 점근선이 없습니다.

반면에, 함수의 수평 점근선은 함수의 무한 극한의 결과가 될 것입니다. 아직:

$\displaystyle \lim_{x \to +\infty} \ x^3-3x^2+4 =(+\infty)^3 = +\infty$

함수의 무한한계는 +무한대를 제공하므로 함수에는 수평 점근선이 없습니다.

이제 경사 점근선을 계산합니다. 경사 점근선의 형식은 다음과 같습니다.

$y=mx+n.$

그리고

$m$

다음 공식으로 계산됩니다.

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \left( x^3-3x^2+4\right): x =$

$\displaystyle = \lim_{x \to +\infty} \cfrac{x^3-3x^2+4}{x} = \cfrac{+\infty}{+\infty} = +\infty$

극한은 우리에게 +무한대를 주므로 함수에는 경사 점근선도 없습니다.

함수의 단조성을 연구하려면 먼저 함수의 도함수를 계산해야 합니다.

$f(x)= x^3-3x^2+4 \ \longrightarrow \ f'(x)= 3x^2-6x$

이제 도함수를 0으로 설정하고 방정식을 풉니다.

$f'(x)= 0$

$3x^2-6x=0$

$x(3x-6)=0$

$\displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}$

이제 얻은 모든 특이점, 즉 영역에 속하지 않는 점(이 경우 모두 속함)과 도함수를 취소하는 점(x=0 및 x =2)을 수직선에 나타냅니다. :

그리고 각 간격에서 도함수의 부호를 평가하여 함수가 증가하는지 감소하는지 확인합니다. 따라서 우리는 각 간격에서 점(특이점은 아님)을 취하고 이 점에서 도함수가 어떤 부호를 갖는지 살펴봅니다.

$f'(-1)=3(-1)^2-6(-1)= 3+6 = 9\ \rightarrow \ \bm{+}$

$f'(1)=3\cdot 1^2-6\cdot 1= 3-6 = -3\ \rightarrow \ \bm{-}$

$f'(3)=3\cdot 3^2-6\cdot 3= 27-18 = 9\ \rightarrow \ \bm{+}$

도함수가 양수이면 함수가 증가한다는 의미이고, 도함수가 음수이면 함수가 감소한다는 의미입니다. 따라서 성장 및 쇠퇴 간격은 다음과 같습니다.

성장:

$\bm{(-\infty,0)\cup (2,+\infty)}$

감소하다:

$\bm{(0,2)}$

함수는 x=0에서 증가에서 감소로 이동하므로 x=0은 함수의 최대값입니다. 그리고 함수는 x=2에서 감소에서 증가로 이동하므로 x=2는 함수의 최소값입니다.

마지막으로 점의 Y 좌표를 찾기 위해 원래 함수에서 찾은 극단을 대체합니다.

$f(0)=0^3-3\cdot 0^2+4 = 4 \ \longrightarrow \ (0,4)$

$f(2)=2^3-3\cdot 2^2+4 = 8-3 \cdot 4 +4 = 0 \ \longrightarrow \ (2,0)$

따라서 함수의 상대적 극단은 다음과 같습니다.

포인트 최대값

$\bm{(0,4)}$

포인트까지의 최소

$\bm{(2,0)}$

함수의 곡률을 연구하기 위해 2차 도함수를 계산합니다.

$f'(x)= 3x^2-6x \ \longrightarrow \ f''(x)= 6x-6$

이제 2차 도함수를 0으로 설정하고 방정식을 풉니다.

$f''(x)= 0$

$6x-6=0$

$6x=6$

$x= \cfrac{6}{6} = 1$

우리는 발견된 모든 특이점, 즉 영역에 속하지 않는 점(이 경우 모두 속함)과 도함수를 취소하는 점(x=1)을 선에 나타냅니다.

이제 각 간격에서 2차 도함수의 부호를 평가하여 함수가 오목인지 볼록인지 확인합니다. 따라서 우리는 각 구간에서 한 점(특이점은 아님)을 취하고 이 점에서 2차 도함수의 부호가 무엇인지 살펴봅니다.

$f''(0)=6\cdot 0-6= -6 \ \rightarrow \ \bm{-}$

$f''(2)=6\cdot 2-6= 12-6= 6 \ \rightarrow \ \bm{+}$

2차 도함수가 양수이면 함수가 볼록함을 의미합니다.

$(\bm{\cup})$

, 그리고 2차 도함수가 음수이면 이는 함수가 오목함을 의미합니다.

$(\bm{\cap})$

. 따라서 오목 및 볼록 간격은 다음과 같습니다.

볼록한

$(\bm{\cup})$

$\bm{(1,+\infty)}$

오목한

$(\bm{\cap})$

$\bm{(-\infty,1)}$

또한 함수는 x=1에서 오목에서 볼록으로 변경되므로 x=1은 함수의 변곡점입니다.

마지막으로 원래 함수에서 찾은 변곡점을 대체하여 점의 Y 좌표를 찾습니다.

$f(1)=1^3-3\cdot 1^2+ 4= 1 -3 +4 =2 \ \longrightarrow \ (1,2)$

따라서 함수의 전환점은 다음과 같습니다.

전환점:

$\bm{(1,2)}$

마지막으로 계산한 모든 정보를 기반으로 함수 그래프를 작성합니다.

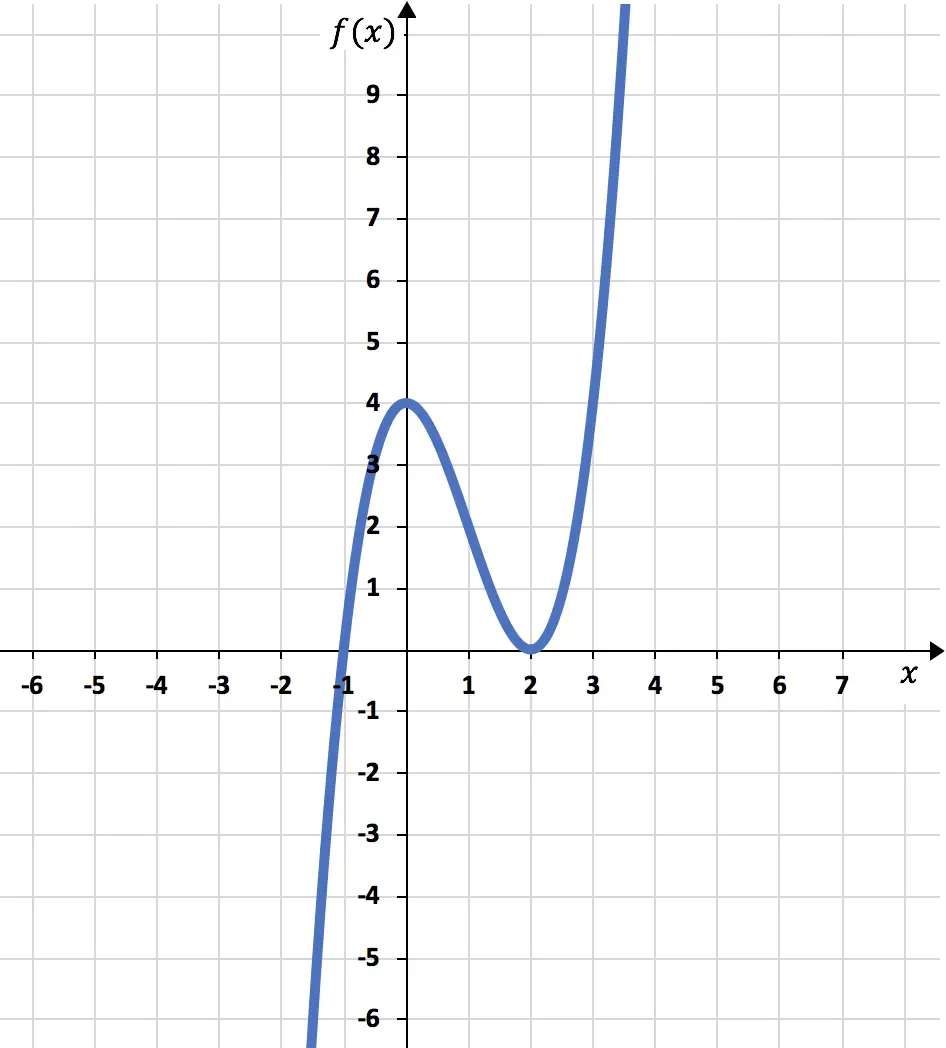
연습 2

다음 유리함수를 그래프로 그려보세요:

$\displaystyle f(x)=\frac{x^2+2}{x^2-1}$

솔루션 보기

함수의 정의역을 찾기 위해 분모를 동일하게 설정합니다. 분수를 0으로 만들고 결과 방정식을 풀어보세요.

$x^2-1= 0$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm 1$

$\text{Dom } f= \mathbb{R}-\{-1, +1 \}$

둘째, 함수의 대수적 표현과 동일한 x축을 사용하여 함수의 임계값을 결정합니다. 강철:

$f(x)=0$

$\cfrac{x^2+2}{x^2-1}=0$

$x^2+2=0\cdot (x^2-1)$

$x^2+2=0$

$x^2=-2$

$x=\sqrt{-2} \quad \color{red}\bm{\times}$

음수의 제곱근은 없습니다. 따라서 함수는 X축과 교차하지 않습니다.

그리고 컴퓨터 축과의 교차점을 찾기 위해 x=0에서 함수를 평가합니다.

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2$

따라서 Y축과의 교차점은 다음과 같습니다.

$\bm{(0,-2)}$

함수에 수직 점근선이 있는지 확인하려면 정의역에 속하지 않는 점(이 경우 x=-1 및 x=+1)에서 함수의 극한을 계산해야 합니다. 그리고 결과가 무한하다면 수직 점근선이 됩니다. 아직:

$\displaystyle \lim_{x \to -1} \cfrac{x^2+2}{x^2-1} = \cfrac{(-1)^2+2}{(-1)^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

x가 -1에 접근할 때 함수의 극한은 무한대를 제공하므로 x=-1은 수직 점근선입니다.

우리는 점근선 x=-1의 측면 한계를 함수에 매우 가까운 숫자로 대체하여 계산합니다:

$\displaystyle f(-1,1)=\cfrac{(-1,1)^2+2}{(-1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to -1^{-}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

$\displaystyle f(-0,9)=\cfrac{(-0,9)^2+2}{(-0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to -1^{+}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

이제 x=+1이 수직 점근선인지 살펴보겠습니다.

$\displaystyle \lim_{x \to +1} \cfrac{x^2+2}{x^2-1} = \cfrac{1^2+2}{1^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

x가 +1에 접근할 때 함수의 극한은 무한대를 제공하므로 x=+1은 수직 점근선입니다.

우리는 점근선 x=1의 측면 한계를 함수에 매우 가까운 숫자로 대체하여 계산합니다:

$\displaystyle f(0,9)=\cfrac{(0,9)^2+2}{(0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to +1^{-}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

$\displaystyle f(1,1)=\cfrac{(1,1)^2+2}{(1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to +1^{+}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

반면에, 함수의 수평 점근선은 함수의 무한 극한의 결과가 될 것입니다. 아직:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2+2}{x^2-1} = \cfrac{+\infty}{+\infty } =\cfrac{1}{1} = 1$

함수의 무한한계는 우리에게 1을 주므로 함수는 y=1에서 수평 점근선을 갖습니다.

함수는 수평 점근선을 가지므로 경사 점근선을 가지지 않습니다.

함수를 미분한 다음 성장과 감소의 간격을 연구합니다.

$f(x)=\cfrac{x^2+2}{x^2-1} \ \longrightarrow \ f'(x)= \cfrac{2x \cdot (x^2-1) -(x^2+2) \cdot 2x}{\left(x^2-1 \right)^2}$

$f'(x)= \cfrac{2x^3-2x - (2x^3+4x) }{\left(x^2-1 \right)^2} = \cfrac{-6x}{\left(x^2-1 \right)^2}$

이제 도함수를 0으로 설정하고 방정식을 풉니다.

$f'(x)= 0$

$\cfrac{-6x}{\left(x^2-1 \right)^2}=0$

$-6x=0\cdot\left(x^2-1 \right)^2$

$-6x= 0$

$x=\cfrac{0}{-6} = 0$

계산된 모든 임계점, 즉 도메인에 속하지 않는 점(x=-1 및 x=+1)과 도함수를 취소하는 점(x=0)을 선에 나타냅니다.

$f'(-2)= \cfrac{-6(-2)}{\left((-2)^2-1 \right)^2} = \cfrac{12}{9} =1,33 \ \rightarrow \ \bm{+}$

$f'(-0,5)= \cfrac{-6(-0,5)}{\left((-0,5)^2-1 \right)^2} = \cfrac{3}{0,56} =5,33 \ \rightarrow \ \bm{+}$

$f'(0,5)= \cfrac{-6\cdot 0,5}{\left(0,5^2-1 \right)^2} = \cfrac{-3}{0,56} =-5,33 \ \rightarrow \ \bm{-}$

$f'(2)= \cfrac{-6\cdot 2}{\left(2^2-1 \right)^2} = \cfrac{-12}{9} =-1,33 \ \rightarrow \ \bm{-}$

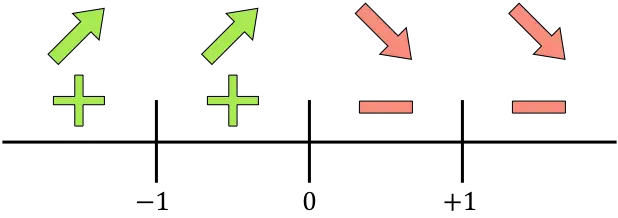
도함수가 양수인 곳에서는 함수가 증가하고 음수인 곳에서는 함수가 감소합니다.

성장:

$\bm{(-\infty,-1)\cup (-1,0)}$

감소하다:

$\bm{(0,1)\cup (1,+\infty)}$

함수는 x=0에서 증가에서 감소로 이동하므로 x=0은 함수의 로컬 최대값입니다.

점의 Y 좌표를 찾기 위해 원래 함수에서 찾은 극값을 대체합니다.

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2 \ \longrightarrow \ (0,-2)$

따라서 함수의 상대적 극단은 다음과 같습니다.

포인트 최대값

$\bm{(0,-2)}$

함수의 곡률을 연구하기 위해 2차 도함수를 계산합니다.

$f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}” title=”Rendered by QuickLaTeX.com”> <p class=$ 모든 용어에는

$(x^2-1)$

, 따라서 분수를 단순화할 수 있습니다.

$f''(x)= \cfrac{-6 \left(x^2-1 \right)^{\cancel{2}} + 24x^2\cancel{(x^2-1)}}{\left(x^2-1 \right)^\cancelto{3}{4}} =\cfrac{-6 \left(x^2-1 \right) + 24x^2}{\left(x^2 -1\right)^3}$

$f''(x)= \cfrac{-6x^2+6 + 24x^2}{\left(x^2 -1\right)^3} =\cfrac{18x^2+6}{\left(x^2 -1\right)^3}$

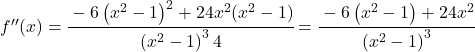
이제 2차 도함수를 0으로 설정하고 방정식을 풉니다.

$f''(x)= 0$

$\cfrac{18x^2+6}{\left(x^2 -1\right)^3}=0$

$18x^2+6=0\cdot \left(x^2 -1\right)^3$

$18x^2+6= 0$

$18x^2=-6$

$x^2=\cfrac{-6}{18}$

$x^2=-0,33$

$x=\sqrt{-0,33} \quad \color{red}\bm{\times}$

음수의 제곱근은 없습니다. 그래서 어울리는 점이 하나도 없네

$f''(x)=0$

이제 우리는 발견된 모든 특이점, 즉 정의역에 속하지 않는 점(x=-1 및 x=+1)과 2차 도함수를 취소하는 점(이 경우에는 존재하지 않는 점)을 선 위에 나타냅니다. 어느):

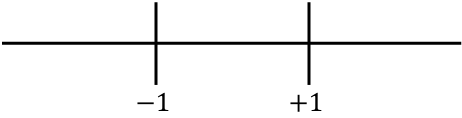
그리고 각 간격에서 2차 도함수의 부호를 평가하여 함수가 오목인지 볼록인지 확인합니다. 따라서 우리는 각 구간에서 한 점(특이점은 아님)을 취하고 이 점에서 2차 도함수의 부호가 무엇인지 살펴봅니다.

$f''(-2)=\cfrac{18(-2)^2+6}{\left((-2)^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

$f''(0)=\cfrac{18\cdot 0^2+6}{\left(0^2 -1\right)^3}= \cfrac{6}{-1} = -6 \ \rightarrow \ \bm{-}$

$f''(2)=\cfrac{18\cdot 2^2+6}{\left(2^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

2차 도함수가 양수이면 함수가 볼록함을 의미합니다.

$(\bm{\cup})$

, 그리고 2차 도함수가 음수이면 이는 함수가 오목함을 의미합니다.

$(\bm{\cap})$

. 따라서 오목 및 볼록 간격은 다음과 같습니다.

볼록한

$(\bm{\cup})$

$\bm{(-\infty, -1) \cup (1, +\infty)}$

오목한

$(\bm{\cap})$

$\bm{(-1,1)}$

그러나 x=-1과 x=1에서 곡률에 변화가 있더라도 이는 변곡점이 아닙니다. 왜냐하면 그들은 기능의 영역에 속하지 않기 때문입니다.

마지막으로 수행된 모든 계산을 사용하여 함수 그래프를 작성합니다.

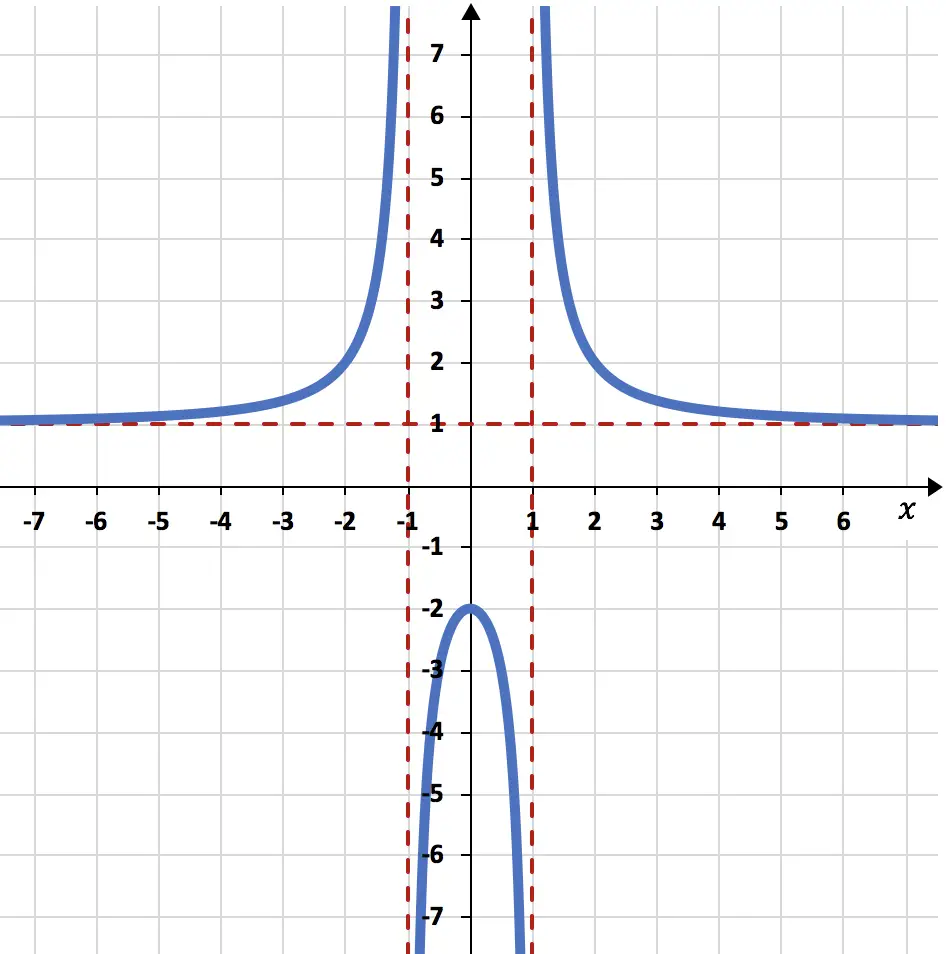
연습 3

다음 유리함수를 그래프에 그려보세요:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

솔루션 보기

이것은 유리함수이므로 함수의 정의역에 속하지 않는 숫자를 확인하려면 분모를 0으로 설정해야 합니다.

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

X축과의 교차점을 찾기 위해 다음을 해결합니다.

$f(x)= 0.$

함수의 X축 값은 항상 0이므로:

$f(x)=0$

$\cfrac{x^3}{x^2-4}=0$

$x^3=0\cdot (x^2-4)$

$x^3=0$

$x=\sqrt[3]{0}=0$

따라서 X축과의 교차점은 다음과 같습니다.

$\bm{(0,0)}$

그리고 Y축과의 교차점을 찾기 위해 다음을 계산합니다.

$f(0).$

x는 Y축에서 항상 0이므로:

$f(0)=\cfrac{0^3}{0^2-4} = \cfrac{0}{-4} = 0$

따라서 Y축과의 교차점은 다음과 같습니다.

$\bm{(0,0)}$

이 경우 함수는 좌표 원점을 통과하므로 X축과의 교점은 Y축과의 교점과 일치합니다.

함수에 수직 점근선이 있는지 확인하려면 정의역에 속하지 않는 점(이 경우 x=-2 및 x=+2)에서 함수의 극한을 계산해야 합니다. 그리고 결과가 무한하다면 수직 점근선이 됩니다. 아직:

$\displaystyle \lim_{x \to -2} \cfrac{x^3}{x^2-4} = \cfrac{(-2)^3}{(-2)^2-4} =\cfrac{-8}{4-4}= \cfrac{-8}{0} = \infty$

x가 -2에 접근할 때 함수의 극한은 무한대를 제공하므로 x=-2는 수직 점근선입니다.

우리는 점근선 x=-2의 측면 한계를 함수에 매우 가까운 숫자로 대체하여 계산합니다:

$\displaystyle f(-2,1)=\cfrac{(-2,1)^3}{(-2,1)^2-4} =-22,59 \longrightarrow \lim_{x \to -2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(-1,9)=\cfrac{(-1,9)^3}{(-1,9)^2-4} =+17,59 \longrightarrow \lim_{x \to -2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

이제 x=+2가 수직 점근선인지 살펴보겠습니다.

$\displaystyle \lim_{x \to +2} \cfrac{x^3}{x^2-4} = \cfrac{(2)^3}{(2)^2-4} =\cfrac{8}{4-4}= \cfrac{8}{0} = \infty$

x가 +2에 접근할 때 함수의 극한은 무한대를 제공하므로 x=+2는 수직 점근선입니다.

우리는 점근선 x=2의 측면 한계를 함수에 매우 가까운 숫자로 대체하여 계산합니다:

$\displaystyle f(1,9)=\cfrac{1,9^3}{1,9^2-4} =-17,59 \longrightarrow \lim_{x \to 2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(2,1)=\cfrac{2,1^3}{2,1^2-4} =22,59 \longrightarrow \lim_{x \to 2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

반면에, 함수의 수평 점근선은 함수의 무한 극한의 결과가 될 것입니다. 아직:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^3}{x^2-4} = \cfrac{+\infty}{+\infty } =+\infty$

함수의 무한한계는 +무한대를 제공하므로 함수에는 수평 점근선이 없습니다.

이제 경사 점근선을 계산합니다. 경사 점근선의 형식은 다음과 같습니다.

$y=mx+n.$

그리고

$m$

다음 공식으로 계산됩니다.

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: x =\lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: \frac{x}{1}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3\cdot 1}{(x^2-4)\cdot x} =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x} = \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

경사 점근선의 기울기를 알고 나면 다음 공식을 사용하여 절편을 결정합니다.

$\displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]$

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

그러나 우리는 불확정성 – 를 얻습니다. 따라서 용어를 공통 분모로 줄이는 것이 필요합니다. 이를 위해 x를 분수의 분모로 곱하고 나눕니다.

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]$

$\displaystyle n = \lim_{x \to +\infty} \cfrac{x^3- (x^3-4x)}{x^2-4} = \lim_{x \to +\infty} \cfrac{4x}{x^2-4}$

$\displaystyle n =\lim_{x \to +\infty} \cfrac{4x}{x^2-4} = \cfrac{+\infty}{\infty} =\bm{0}$

즉, 경사 점근선은 다음과 같습니다.

$y = mx+n$

$y = 1x + 0$

$\bm{y = x }$

함수의 단조성을 연구하려면 먼저 함수의 도함수를 계산해야 합니다.

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

이제 도함수를 0으로 설정하고 방정식을 풉니다.

$f'(x)= 0$

$\cfrac{x^4-12x^2}{\left(x^2-4\right)^2}=0$

$x^4-12x^2=0\cdot \left(x^2-4\right)^2$

$x^4-12x^2=0$

$x^2(x^2-12)=0$

$\displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}$

이제 발견된 모든 특이점, 즉 영역에 속하지 않는 점(x=-2 및 x=+2)과 도함수를 취소하는 점(x=0, x=-)을 선 위에 나타냅니다. 3.46 및 x= +3.46):

$f'(-4)= \cfrac{(-4)^4-12(-4)^2}{\left((-4)^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

$f'(-3)= \cfrac{(-3)^4-12(-3)^2}{\left((-3)^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(-1)= \cfrac{(-1)^4-12(-1)^2}{\left((-1)^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(1)= \cfrac{1^4-12\cdot1^2}{\left(1^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(3)= \cfrac{3^4-12\cdot 3^2}{\left(3^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(4)= \cfrac{4^4-12\cdot 4^2}{\left(4^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

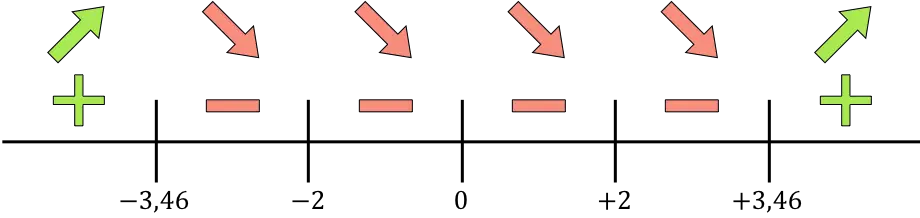
도함수가 양수이면 함수가 증가한다는 의미이고, 도함수가 음수이면 함수가 감소한다는 의미입니다. 따라서 성장 및 쇠퇴 간격은 다음과 같습니다.

성장:

$\bm{(-\infty,-3,46)\cup (3,46,+\infty)}$

감소하다:

$\bm{(-3,46,-2)\cup(-2,0)\cup (0,2) \cup (2,3,46)}$

함수는 x=-3.46에서 증가에서 감소로 이동하므로 x=-3.46은 함수의 최대값입니다. 그리고 함수는 x=3.46에서 감소에서 증가로 이동하므로 x=3.46은 함수의 최소값입니다.

상대 끝의 Y 좌표를 결정합니다.

$f(-3,46)=\cfrac{(-3,46)^3}{(-3,46)^2-4} = \cfrac{-41,42}{7,97}=-5,20 \ \longrightarrow \ (-3,46,-5,20)$

$f(3,46)=\cfrac{3,46^3}{3,46^2-4} = \cfrac{41,42}{7,97}=5,20 \ \longrightarrow \ (3,46,5,20)$

따라서 함수의 상대적 극단은 다음과 같습니다.

포인트 최대값

$\bm{(-3,46,-5,20)}$

포인트까지의 최소

$\bm{(3,46,5,20)}$

함수의 곡률을 연구하기 위해 함수의 2차 도함수를 계산합니다.

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

이제 2차 도함수를 0으로 설정하고 방정식을 풉니다.

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

$x(8x^2+96)=0$

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

실수에는 음의 근이 없기 때문에 해결책이 없습니다.

이제 발견된 모든 특이점, 즉 도메인에 속하지 않는 점(x=-2 및 x=+2)과 2차 도함수를 취소하는 점(x=0)을 선에 나타냅니다.

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot 1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

2차 도함수가 양수이면 함수가 볼록함을 의미합니다.

$(\bm{\cup})$

, 그리고 2차 도함수가 음수이면 이는 함수가 오목함을 의미합니다.

$(\bm{\cap})$

. 따라서 오목 및 볼록 간격은 다음과 같습니다.

볼록한

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

오목한

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

그러나 x=-2 및 x=+2에서 곡률에 변화가 있더라도 이는 변곡점이 아닙니다. 왜냐하면 x=-2와 x=+2는 함수의 정의역에 속하지 않기 때문입니다. 반면, x=0에서는 곡률이 변경되고(함수가 볼록에서 오목으로 이동) 이것이 함수에 속하므로 x=0이 변곡점입니다.

변곡점의 다른 좌표를 찾기 위해 원래 함수에서 찾은 변곡점을 대체합니다.

$f(0) = \cfrac{0^3}{0^2-4} = \cfrac{0}{-4} =0\ \longrightarrow \ (0,0)$

따라서 함수의 전환점은 다음과 같습니다.

전환점:

$\bm{(0,0)}$

마지막으로 계산한 모든 정보를 바탕으로 함수를 표현합니다.

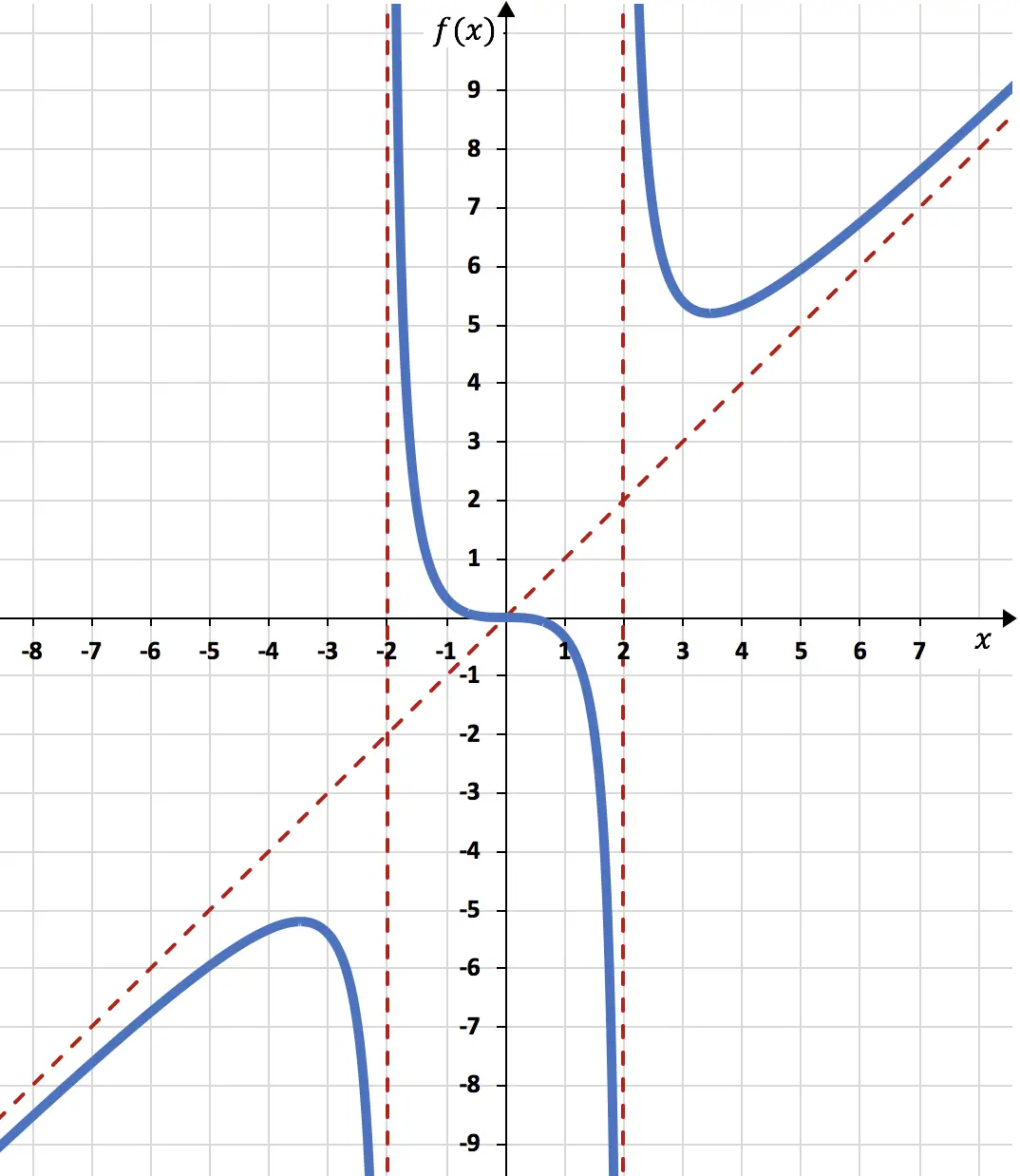
설명: 함수가 점에서 경사 점근선을 교차한다는 점에 유의하세요.

$(0,0) .$

실제로, 경사 점근선은 무엇보다도 x가 + 과 – 을 향할 때 함수의 동작을 결정합니다. 사실, 함수는 그래프의 오른쪽(x→+무한대)과 그래프의 왼쪽에 있는 경사 점근선을 결코 교차하지 않습니다. 그래프(x→-무한대). 그러나 함수가 중간에서 경사 점근선을 교차하는 경우는 매우 드물며 매우 특별한 경우입니다.

그래프에 함수를 표현하는 방법

함수 표현의 예

함수를 표현하는 연습문제 해결

연습 1

연습 2

연습 3

댓글 달기 댓글 취소