기능을 이용한 연산: 덧셈, 뺄셈, 곱, 나눗셈, 합성

9월 17, 2023

이 글에서는 함수를 사용하여 어떤 작업을 수행할 수 있는지 설명합니다. 기능을 이용한 조작에 대한 설명과 해결 연습을 볼 수 있습니다. 마지막으로 함수를 사용하여 작업의 속성을 찾을 수 있습니다.

함수를 사용한 작업이란 무엇입니까?

덧셈, 뺄셈, 곱셈, 나눗셈, 합성 등 5가지 다른 유형의 기능을 수행할 수 있습니다. 즉, 두 개의 함수를 더하거나 빼거나 곱하거나 나누거나 합성할 수 있습니다.

다음으로 각 유형의 작업이 어떻게 기능과 각각의 특징으로 수행되는지 살펴보겠습니다.

함수의 합

두 함수의 합(또는 더하기) 값은 각 함수 값의 합과 같습니다. 즉, 합계 함수의 이미지를 계산하려면 연산에 관련된 함수의 이미지를 추가하기만 하면 됩니다.

$(f+g)(x)=f(x)+g(x)$

또한, 두 함수의 합의 정의역은 각 합산된 함수 정의역의 교집합입니다.

$\text{Dom}(f+g)=\text{Dom}(f)\cap\text{Dom}(g)$

예제를 사용하여 두 함수가 어떻게 추가되는지 살펴보겠습니다.

$f(x)=x^2+1 \qquad g(x)=\log(x-1)$

먼저 두 가지 기능을 추가합니다.

$(f+g)(x)=f(x)+g(x)=x^2+1+\log(x-1)$

이제 우리는 sum 함수의 정의역을 찾습니다. 이를 위해 각 함수의 도메인을 개별적으로 계산합니다.

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=(1,+\infty)$

➤ 참고: 함수의 정의역을 계산하는 방법

그러면 연산으로 인한 함수의 도메인은 다음과 같습니다.

$\text{Dom}(f+g)=\text{Dom}(f)\cap\text{Dom}(g)=(1,+\infty)$

함수가 포함된 각 작업에는 결과를 완전히 정의하기 위해 해당 도메인이 수반되어야 합니다.

함수 빼기

두 함수의 빼기(또는 차이) 이미지는 작업에 참여하는 각 함수의 이미지를 빼는 것입니다.

$(f-g)(x)=f(x)-g(x)$

덧셈 함수와 마찬가지로 두 함수의 뺄셈 영역은 각 함수 영역의 교차점과 동일합니다.

$\text{Dom}(f-g)=\text{Dom}(f)\cap\text{Dom}(g)$

따라서 독립변수 x의 특정 값에서 함수가 정의되지 않으면 뺄셈에 따른 함수도 정의되지 않습니다.

예제를 통해 두 함수를 어떻게 빼는지 살펴보겠습니다.

$f(x)=\sqrt{x}\qquad g(x)=\cfrac{3}{x-4}$

먼저 두 함수를 뺍니다.

$(f-g)(x)=f(x)-g(x)=\sqrt{x}-\cfrac{3}{x-4}$

그런 다음 빼기 함수의 영역을 결정합니다.

$\text{Dom}(f)=[0,+\infty)\qquad\text{Dom}(g)=\mathbb{R}-\{4\}$

$\text{Dom}(f-g)=\text{Dom}(f)\cap\text{Dom}(g)=[0,4)\cup (4,+\infty)$

주력 제품

두 함수의 곱 또는 곱셈을 계산하려면 각 함수의 표현식을 곱하기만 하면 됩니다.

$(f\cdot g)(x)=f(x)\cdot g(x)$

반면, 곱함수의 정의역은 각 곱셈 함수의 정의역의 교점 집합입니다.

$\text{Dom}(f\cdot g)=\text{Dom}(f)\cap\text{Dom}(g)$

예를 들어 다음과 같은 두 가지 기능이 있다고 가정해 보겠습니다.

$f(x)=\sqrt[3]{x^2-1}\qquad g(x)=\cfrac{2}{3x+6}$

먼저, 다음 두 가지 기능으로 제품의 작동을 수행합니다.

$(f\cdot g)(x)=f(x)\cdot g(x)=\sqrt[3]{x^2-1}\cdot\cfrac{2}{3x+6}=\cfrac{2\sqrt[3]{x^2-1}}{3x+6}$

그리고 마지막으로 연산의 결과로 함수의 영역을 찾습니다.

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=\mathbb{R}-\{-2\}$

$\text{Dom}(f\cdot g)=\text{Dom}(f)\cap\text{Dom}(g)=(-\infty,-2)\cup (-2,+\infty)$

기능의 분포

두 함수의 나눗셈(또는 몫) 의 수치 결과는 다음 방정식에 해당합니다.

$\displaystyle\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}$

그러나 두 함수의 나눗셈 영역은 각 함수의 영역에서 모든 x를 뺀 교차점 집합으로, 제수 역할을 하는 함수를 취소합니다. 그렇지 않으면 불확정성을 얻게 되기 때문입니다.

$\displaystyle\text{Dom}\left(\frac{f}{g}\right)(x)=\text{Dom}(f)\cap\text{Dom}(g)-\{x:g(x)=0\}$

예를 들어 다음과 같은 기능을 나누어 보겠습니다.

$f(x)=5^x \qquad g(x)=x-3$

기능의 분포는 다음과 같습니다.

$\displaystyle\left(\frac{f}{g}\right)(x)=\frac{f(x)}{g(x)}=\cfrac{5^x}{x-3}$

반면, 각 함수의 정의역은 개별적으로 모든 실수로 구성됩니다.

$\text{Dom}(f)=\mathbb{R}\qquad\text{Dom}(g)=\mathbb{R}$

그러나 분수의 분모에는 0이 있을 수 없으므로 결과 함수의 영역에서는 분모(x=3)를 상쇄하는 모든 값을 제거해야 합니다.

$\displaystyle\text{Dom}\left(\frac{f}{g}\right)(x)=\text{Dom}(f)\cap\text{Dom}(g)-\{x:g(x)=0\}=\mathbb{R}-\{3\}$

기능의 구성

함수의 합성은 가장 복잡한 개념이기 때문에 해결하기 가장 어려운 작업이다.

기능 구성은 두 가지 기능의 연속적인 적용으로 구성됩니다. 대수적으로 두 함수의 구성은 다음과 같이 표현됩니다.

$(g\circ f)(x)=g\Bigl(f(x)\Bigr)$

반면에, 기능의 구성 영역은

$(g\circ f)(x)$

함수 정의역에서 x의 모든 값의 집합과 동일합니다.

$f$

~와 같은

$f(x)$

기능의 영역에 속한다

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

예를 들어 다음 두 가지 함수가 있다고 가정해 보겠습니다.

$f(x)=x^2+1 \qquad g(x)=3x-4$

복합 함수를 찾으려면

$f$

이어서

$g$

우리는 표현을 바꿔야합니다

$f(x)$

어디 하나 있어요

$x$

의 표현에서

$g(x):$

$\begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}$

이 경우 두 함수의 정의역은 모두 실수로 구성되므로 합성 함수의 정의역도 실수로 구성됩니다.

$\text{Dom}(g\circ f)=\mathbb{R}$

보시다시피, 함수를 구성하는 것은 이해하기 쉬운 간단한 작업이 아닙니다. 따라서 다음과 같은 함수 구성 연습을 연습하는 것이 좋습니다.

➤ 참조: 기능 구성에 대한 해결 연습

함수를 사용한 작업의 속성

함수를 사용한 모든 연산 중에서 합계와 곱은 다음 속성이 특징입니다.

결합속성 : 3개 이상의 기능을 더하거나 곱하는 순서는 상관없습니다.

$f(x)+\bigl[g(x)+h(x)\bigr]=\bigl[f(x)+g(x)\bigr]+h(x)$

$f(x)\cdot \bigl[g(x)\cdot h(x)\bigr]=\bigl[f(x)\cdot g(x)\bigr] \cdot h(x)$

교환 속성 : 두 함수의 덧셈이나 곱셈의 순서는 결과를 수정하지 않습니다.

$f(x)+g(x)=g(x)+f(x)$

$f(x)\cdot g(x)=g(x)\cdot f(x)$

중립 요소: 합 연산과 곱 연산은 일정한 중립 요소 기능을 갖습니다.
$f(x)=0$

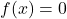
그리고

$f(x)=1$

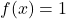
각기.

대칭 요소 : 합계 함수는 반대 함수를 가집니다.
$-f(x).$

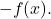
분배 속성 : 이 속성은 연산의 합과 곱을 연결하며 다음 동등성을 기반으로 합니다.

$f(x)\cdot \bigl[g(x)+h(x)\bigr]=f(x)\cdot g(x)+f(x)\cdot h(x)$

댓글 달기 댓글 취소