평행선 - 마토리티

여기에서는 평행선에 대한 모든 것을 찾을 수 있습니다: 평행선의 의미, 두 선이 평행한지 확인하는 방법, 해당 속성 등. 또한 평행선에 대한 몇 가지 예와 해결 연습을 볼 수 있습니다.

평행선이란 무엇입니까?

평행선은 결코 교차하지 않는 선입니다. 즉, 궤적이 무한대로 확장되어도 서로 닿지 않습니다. 따라서 두 평행선의 점은 항상 서로 같은 거리를 가지며, 더욱이 두 평행선에는 공통점이 없습니다.

예를 들어, 다음 두 줄은 평행합니다.

우리는 일반적으로 두 개의 선이 2개의 수직 막대 ||와 평행함을 나타냅니다. 줄 사이

반면에 두 개의 평행선은 결코 교차하지 않는다는 사실에도 불구하고 분석기하학에서는 두 평행선이 동일한 방향을 가지므로 0°의 각도를 형성한다고 말합니다.

두 선이 평행할 때는 언제인가?

평행선의 정의를 확인한 후에는 두 개의 평행선을 찾는 방법을 살펴보겠습니다. 분명히 한 가지 방법은 선을 그래프로 그려 그래프에서 교차하는지 확인하는 것이지만, 훨씬 더 간단하고 사용하기 쉬운 방법이 있습니다.

기울기를 사용하여 두 선의 평행도 결정

각 선의 기울기를 보면 두 선이 평행한 때를 알 수 있습니다. 선의 기울기가 매개변수라는 점을 기억하세요.

$m$

명시적 방정식과 선의 점-기울기 방정식에서:

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

그러나 선의 기울기를 결정하는 방법에는 여러 가지가 있으므로 이를 계산하는 방법을 알아보려면 선의 기울기 공식을 살펴보는 것이 좋습니다. 또한, 링크된 페이지에서는 선의 기울기가 무엇을 나타내는지, 그리고 그것이 선에서 왜 그렇게 중요한지에 대한 설명도 찾을 수 있습니다.

따라서 평면에서 두 직선의 기울기(계수 m)는 동일 하고 원점(계수 n)의 좌표는 서로 다르면 평행합니다 .

예를 들어, 다음 두 줄은 평행합니다.

$r: \ y=5x+1 \qquad \qquad s: \ y=5x-3$

두 직선은 기울기가 같고 독립항도 다르기 때문에 평행선입니다.

$m_r =m_s =5$

$n_r =1 \neq n_s =-3$

두 선이 동일한 기울기를 가지며 동시에 원점에서 동일한 컴퓨터를 갖는다면 두 선은 정확히 동일하기 때문에 동일한 선이 됩니다.

암시적 방정식에서 두 선의 평행성을 찾아보세요.

직선의 암시적(또는 일반) 방정식은 다음과 같습니다.

$Ax+By+C=0$

따라서 두 직선의 계수 A와 B가 서로 비례하고 계수 C에 비례하지 않으면 직선이 평행하다는 의미입니다.

$r: \ Ax+By+C=0 \qquad \qquad s: \ A'x+B'y+C'=0$

$\cfrac{A}{A'} = \cfrac{B}{B'} \neq \cfrac{C}{C'} \quad \bm{\longrightarrow} \quad r \parallel s$

다음은 일반(또는 암시적) 방정식 형식으로 표현된 두 개의 평행선입니다.

$r: \ 4x-6y+7=0 \qquad \qquad s: \ -2x+3y-1=0$

변수 앞의 숫자가 평행하므로

$x$

변수 앞의 숫자에 비례한다

$y$

, 그러나 독립적인 용어는 아닙니다.

$\cfrac{4}{-2} = \cfrac{-6}{3} = -2 \neq \cfrac{7}{-1}=-7$

이전과 마찬가지로 두 암시적 선의 모든 계수(A, B 및 C)가 비례한다면 이는 두 선이 일치한다는 것을 의미합니다. 즉, 두 선이 동일하다는 것을 의미합니다.

평행선의 속성

평행선의 특징은 다음과 같습니다.

대칭성 : 한 선이 다른 선과 평행하면 이 선도 첫 번째 선과 평행합니다. 이 속성은 수직선에도 적용됩니다.

$r \parallel s \ \longrightarrow \ s \parallel r$

추이적 속성 : 한 선이 다른 선과 평행하고 이 두 번째 선이 세 번째 선과 평행하면 첫 번째 선도 세 번째 선과 평행합니다.

$\left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q$

두 평행선의 방향 벡터(선의 방향을 나타내는 벡터)의 스칼라 곱은 해당 모듈의 곱과 같습니다.

$r \parallel s \ \longrightarrow \ \vv{\text{v}}_r \cdot \vv{\text{v}}_s= \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{\text{v}}_s \rvert$

또한 두 평행선의 방향 벡터는 비례하기 때문에 항상 서로 선형 종속 입니다.

이 조건은 선이 평행하려면 필요하지만 충분하지는 않습니다. 즉, 두 평행선은 비례적인 방향 벡터를 가져야 하지만 두 선이 비례 방향 벡터를 갖는다고 해서 두 선이 평행하다는 것을 직접적으로 의미하지는 않습니다. 일치하는 선에도 비례하는 방향 벡터가 있기 때문입니다.

가로축(X축)에 평행한 선은 수평이며 항상 다음과 같은 형태를 갖습니다.
$y=k.$

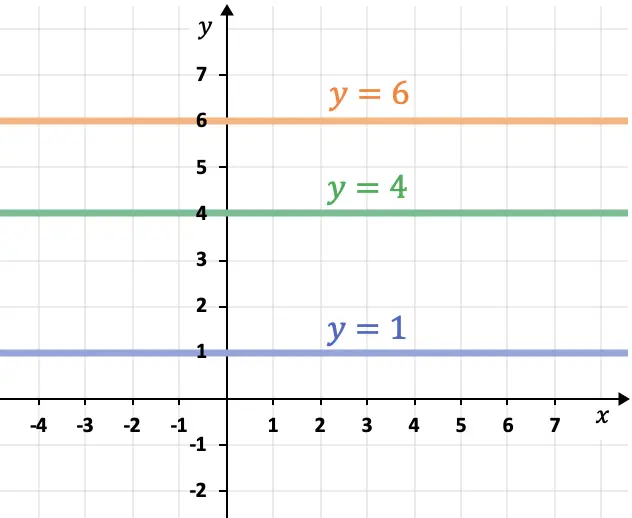
컴퓨터 축(Y축)에 평행한 선은 수직이며 항상 다음 식을 따릅니다.
$x=k.$

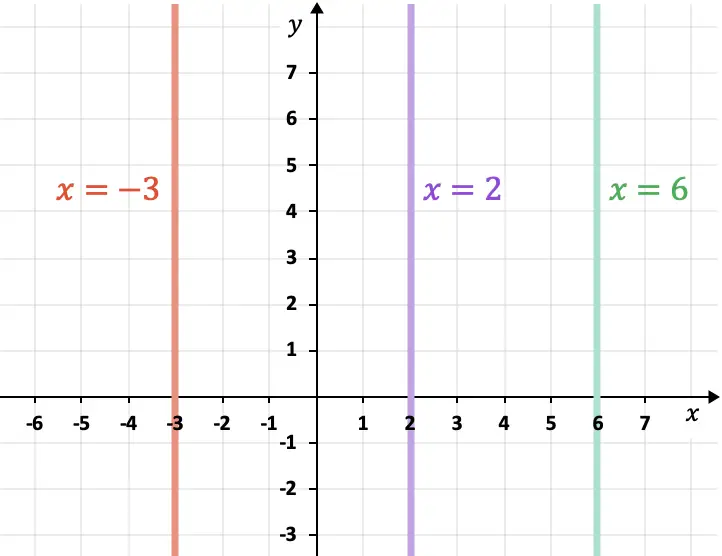
평면에서 두 평행선 사이의 거리를 계산하는 방법

평면(R2)에서 두 평행선 사이의 거리를 찾으려면 두 선 중 하나에 점을 가져다가 이 점에서 다른 선까지의 거리를 계산하면 됩니다.

두 개의 평행선은 항상 같은 거리만큼 떨어져 있기 때문에 이렇게 할 수 있습니다.

반면, 공식을 사용하여 거리가 0 단위가 되면 이는 선이 어떤 지점에서 서로 접촉하므로 선이 평행하지 않고 교차하거나 일치하거나 수직임을 의미합니다. 원하는 경우 당사 웹사이트에서 이러한 유형의 라인 간의 차이점을 확인할 수 있습니다.

따라서 이것이 어떻게 수행되는지 볼 수 있도록 예를 들어 다음 두 평행선 사이의 거리를 결정하겠습니다.

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

가장 먼저 해야 할 일은 선 중 하나(원하는 선)에 점을 찍는 것입니다. 이 경우 선 위의 점을 계산하겠습니다.

$s.$

이렇게 하려면 변수 중 하나에 값을 지정해야 합니다. 예를 들어 다음과 같이 하겠습니다.

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

이제 다른 변수(

$y$

) 이 시점에서 그것이 얼마나 가치가 있는지 알기 위해 얻은 방정식:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

따라서 직선에서 얻은 점은

$s$

동쪽:

$P(0,-2)$

그리고 선 위에 이미 점이 있으면 점에서 선까지의 거리 공식을 사용하여 해당 점에서 다른 선까지의 거리를 계산합니다.

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{\lvert 0+8-6\rvert}{\sqrt{4+16}}={\cfrac{2}{\sqrt{20}}=\bm{0,45}$