평면의 벡터 방정식

이 페이지에서는 평면 벡터 방정식(공식)과 계산 예를 찾을 수 있습니다. 또한 평면의 벡터방정식에 대한 연습문제와 해결문제를 통해 연습할 수 있습니다.

평면의 벡터 방정식은 무엇입니까?

해석기하학에서 평면의 벡터방정식은 어떤 평면이라도 수학적으로 표현할 수 있게 해주는 방정식이다. 평면의 벡터 방정식을 찾으려면 점 하나와 해당 평면에 속하는 두 개의 선형 독립 벡터만 있으면 됩니다.

평면의 벡터 방정식의 공식

평면의 점과 두 방향 벡터를 고려하십시오.

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

평면의 벡터 방정식의 공식은 다음과 같습니다.

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

금

$\lambda$

그리고

$\mu$

는 두 개의 스칼라, 즉 두 개의 실수를 의미합니다.

따라서 이는 평면의 모든 점은 1개의 점과 2개의 벡터의 선형 조합으로 표현될 수 있음을 의미합니다.

또한 앞의 방정식이 평면에 대응하기 위한 필요조건은 평면의 두 벡터가 선형독립성을 갖는 것, 즉 두 벡터가 서로 평행할 수 없다는 것이다. 다른.

한편, 벡터 방정식 외에도 평면의 매개방정식, 평면의 암시적 방정식 등 평면을 해석적으로 표현하는 다른 방법이 있다는 점을 명심하세요. 링크에서 각 방정식 유형이 무엇인지 확인할 수 있습니다.

평면의 벡터 방정식을 찾는 방법의 예

평면의 벡터 방정식 개념에 대한 설명을 확인한 후 예제를 통해 이것이 어떻게 계산되는지 살펴보겠습니다.

점을 통과하는 평면의 벡터 방정식을 구합니다.
$P(2,0,4)$

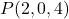
그리고 벡터를 포함합니다

$\vv{\text{u}}=(1,3,-2)$

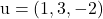
그리고

$\vv{\text{v}}=(5,0,1).$

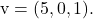
평면의 벡터 방정식을 결정하려면 해당 공식을 적용하면 됩니다.

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

이제 점과 각 벡터를 방정식으로 대체합니다.

$\bm{(x,y,z)=(2,0,4)+\lambda (1,3,-2) + \mu (5,0,1)}$

예제에서 볼 수 있듯이 평면의 벡터 방정식을 찾는 것은 비교적 쉽습니다. 그러나 문제가 약간 복잡해질 수 있으므로 아래에는 연습할 수 있도록 다양한 난이도의 몇 가지 해결된 연습 문제가 있습니다.

평면 벡터 방정식으로 문제 해결

연습 1

벡터를 포함하는 평면의 벡터 방정식을 결정합니다.

$\vv{\text{u}}=(0,-2,3)$

다음 두 가지 사항을 살펴봅니다.

$A(1,3,-1)$

그리고

$B(2,-1,5).$

해결책 보기

평면의 방정식을 알려면 점 하나와 벡터 두 개가 필요합니다. 이 경우 벡터는 하나뿐이므로 평면의 또 다른 방향 벡터를 찾아야 합니다. 이를 위해 평면의 두 점을 정의하는 벡터를 계산할 수 있습니다.

$\vv{AB} = B - A = (2,-1,5) - (1,3,-1) = (1,-4,6)$

이제 우리는 평면과 점의 두 방향 벡터를 이미 알고 있으므로 평면의 벡터 방정식에 대한 공식을 사용합니다.

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

그리고 두 벡터와 평면의 두 점 중 하나를 방정식으로 대체합니다.

$\bm{(x,y,z)=(1,3,-1)+\lambda (0,-2,3) + \mu (1,-4,6)}$

연습 2

다음 세 점을 포함하는 평면의 벡터 방정식을 구합니다.

$A(2,-2,1) \qquad B(1,0,4) \qquad C(-1,3,-2)$

해결책 보기

평면의 벡터 방정식을 찾으려면 평면에 결합하는 두 개의 선형 독립 벡터를 찾아야 합니다. 그리고 이를 위해 3개의 점으로 정의되는 두 개의 벡터를 계산할 수 있습니다.

$\vv{AB} = B - A = (1,0,4) - (2,-2,1) = (-1,2,3)$

$\vv{AC} = C - A = (-1,3,-2) - (2,-2,1) = (-3,5,-3)$

발견된 두 벡터의 좌표는 비례하지 않으므로 서로 선형 독립입니다.

이제 우리는 이미 두 개의 방향 벡터와 평면의 한 점을 알고 있으므로 평면의 벡터 방정식에 대한 공식을 적용합니다.

$(x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}}$

그리고 두 벡터와 평면의 세 점 중 하나를 방정식에 대체합니다.

$\bm{(x,y,z)=(2,-2,1)+\lambda (-1,2,3) + \mu (-3,5,-3)}$

연습 3

다음 벡터 방정식으로 정의된 평면에 속하는 공간의 4개 점을 계산합니다.

$(x,y,z)=(0,2,1)+\lambda (2,-1,4) + \mu (-1,3,0)$

해결책 보기

평면의 점을 계산하려면 매개변수에 값을 지정하면 됩니다.

$\lambda$

그리고

$\mu .$

아직:

$\left. \begin{array}{c} \lambda =0 \\[2ex] \mu =0 \end{array} \right\} \longrightarrow \ (0,2,1)+0\cdot (2,-1,4) + 0\cdot (-1,3,0)= \bm{(0,2,1)}$

$\left. \begin{array}{c} \lambda =1 \\[2ex] \mu =0 \end{array} \right\} \longrightarrow \ (0,2,1)+1\cdot (2,-1,4) + 0\cdot (-1,3,0)= \bm{(2,1,5)}$

$\left. \begin{array}{c} \lambda =0 \\[2ex] \mu =1 \end{array} \right\} \longrightarrow \ (0,2,1)+0\cdot (2,-1,4) + 1\cdot (-1,3,0)= \bm{(-1,5,1)}$

$\left. \begin{array}{c} \lambda =1 \\[2ex] \mu =1 \end{array} \right\} \longrightarrow \ (0,2,1)+1\cdot (2,-1,4) + 1\cdot (-1,3,0)= \bm{(1,4,5)}$

연습 4

직선을 포함하는 평면의 벡터 방정식을 구합니다.

$r$

그리고 오른쪽과 평행하다

$s.$

라인 :

$\displaystyle r: \ \begin{cases} x=4+2t \\[1.7ex] y=-1+t\\[1.7ex] z=5-4t \end{cases} \qquad \qquad s: \ \frac{x-1}{2} = \frac{y+2}{4}= \frac{z+1}{-3}$