▷ 평균 및 순간 변화율(해결된 연습문제)

여기서는 변화율, 평균변화율, 순간변화율이 무엇인지 설명하겠습니다. 변화율을 계산하는 방법에 대한 몇 가지 예를 볼 수 있으며, 또한 변화율에 대한 단계별 연습 문제를 해결하여 연습할 수 있습니다.

변화율은 얼마입니까?

수학에서 함수의 변화율(TV)은 서로 다른 두 지점에서 함수 값의 차이입니다. 따라서 두 지점 사이의 변화율을 계산하려면 이 두 지점의 함수 값을 빼야 합니다.

$\text{TV}[a,b]=f(b)-f(a)$

예를 들어, 함수의 두 이미지가 f(2)=1 및 f(5)=7인 경우 변화율은 다음과 같습니다.

$\text{TV}[2,5]=f(5)-f(2)=7-1=6$

우리는 방금 변화율의 수학적 의미를 살펴보았지만, 경제학에서 변화율의 개념은 다음을 의미합니다.

경제학에서 두 값 사이의 변화율은 백분율로 표시되는 두 값의 차이입니다. 즉, 서로 다른 기간 사이의 변수 변화율은 상대적인 변화입니다. 따라서 변화율을 계산하려면 서로 다른 두 기간의 값을 빼고 얻은 결과를 초기 기간의 값으로 나눕니다.

$\text{TV}[t,t+n]=\cfrac{Y_{t+n}-Y_t}{Y_t}\cdot 100$

예를 들어 특정 주식의 가치가 한 달에 €35에서 €50로 증가한 경우 변화율은 다음과 같습니다.

$\text{TV}[t,t+1]=\cfrac{50-35}{35}\cdot 100=42,86 \ \%$

변화율의 두 가지 가능한 의미를 고려하여 이 기사에서는 변화율의 수학적 정의를 이해하는 데 중점을 둘 것입니다. 변화율에는 평균변화율과 순간변화율이라는 두 가지 유형이 있습니다. 아래에는 각 유형에 대한 설명이 나와 있습니다.

평균 변화율

구간 내 함수의 평균 변화율(TVM)은 독립 변수가 증가하는 각 단위에 대해 함수가 증가(또는 감소)하는 단위 수입니다. 따라서 함수의 평균 변화율은 구간 내 함수의 증가를 동일한 구간의 진폭으로 나누어 계산됩니다.

$\text{TVM}[a,b]=\cfrac{f(b)-f(a)}{b-a}$

평균 변화율이 어떻게 계산되는지 확인할 수 있도록 아래 예제를 단계별로 해결했습니다.

함수의 평균 변화율을 계산하는 예

다음 함수의 간격 [2.5]에서 평균 변화율을 계산합니다.

$f(x) = x^2-1$

먼저 x=2 및 x=5에서 함수의 값을 계산합니다.

$f(5)= 5^2-1=25-1=24$

$f(2)=2^2-1=4-1=3$

그런 다음 다음 공식을 적용하여 구간 내 함수의 평균 변화율을 계산합니다.

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,5]=\cfrac{f(5)-f(2)}{5-2} = \cfrac{24 - 3}{5-2} = \cfrac{21}{3} = \bm{7}$

TVM[2,5]의 결과가 양수이므로 이는 함수가 [2,5] 구간에서 증가한다는 의미입니다. 반면에 결과가 음수인 경우 이는 이 간격에서 함수가 감소한다는 의미입니다.

평균 변화율의 기하학적 해석

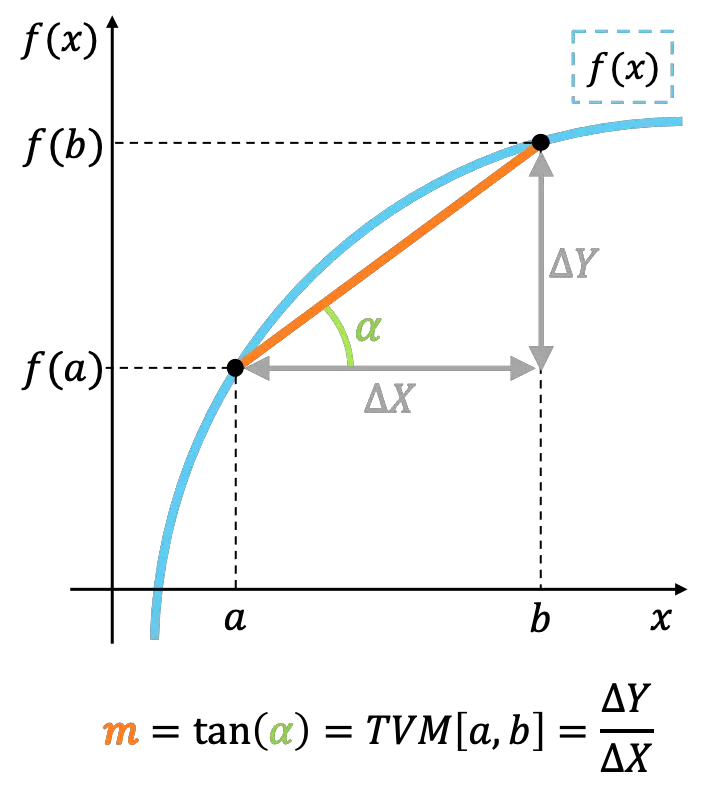
기하학적으로 구간 내 함수의 평균 변화율은 구간의 극단 점을 연결하는 선의 기울기를 나타냅니다.

순간 변화율

한 지점에서 함수의 순간 변화율(TVI)은 간격에 따른 함수의 상대적 증가의 극미한 한계입니다. 따라서 순간 변화율은 h 가 0에 접근 하도록 f(a+h)-f(a) 의 몫의 극한을 풀어 계산됩니다.

$\displaystyle\text{TVI}(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$

순간 변화율의 값은 양수, 음수 또는 0일 수 있으며, 이는 해당 지점의 함수가 해당 지점에서 각각 증가, 감소 또는 동일하게 유지됨을 의미합니다.

함수의 순간 변화율 계산 예

다음 함수의 x=2 지점에서 순간 변화율을 계산합니다.

$f(x) = x^2$

순간 변화율을 계산하려면 다음 공식을 적용해야 합니다.

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h} = \lim\limits_{h \to 0} \cfrac{(2+h)^2-2^2}{h}$

우리는 주목할만한 정체성을 해결합니다:

$\lim\limits_{h \to 0} \cfrac{2^2+h^2+2\cdot 2 \cdot h -2^2}{h} = \lim\limits_{h \to 0} \cfrac{4+h^2+4h -4}{h} = \lim\limits_{h \to 0} \cfrac{h^2+4h}{h}$

➤ 주목할 만한 항등식에 대한 공식을 더 이상 기억하지 못하는 경우 다항식 전문 사이트인 www.polinomios.org 에서 모든 공식을 찾을 수 있습니다.

이제 한계를 해결해 보겠습니다.

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h} = \cfrac{0^2+4\cdot 0}{0} =\cfrac{0}{0}$

그러나 우리는 0 사이에 0의 불확정성을 발견합니다. 따라서:

$\lim\limits_{h \to 0} \cfrac{h^2+4h}{h}= \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+4)}{\cancel{h}} = \lim\limits_{h \to 0} (h+4)$

➤ 참조: 0 사이의 불확정성이 0인 극한을 해결하는 방법

그리고 마지막으로 한계를 해결합니다.

$\lim\limits_{h \to 0} (h+4) = 0 +4 = \bm{4}$

아직:

$\mathbf{TVI} \bm{(2) = 4}$

TVI(2)의 결과가 양수이므로 이는 x=2에서 함수가 증가한다는 의미입니다. 반면에 결과가 부정적이었다면 이는 이 단계에서 기능이 감소하고 있음을 의미합니다.

순간변화율의 기하학적 해석

기하학적으로 한 점에서 함수의 순간 변화율은 같은 점에서 함수에 접하는 선의 기울기를 나타냅니다.

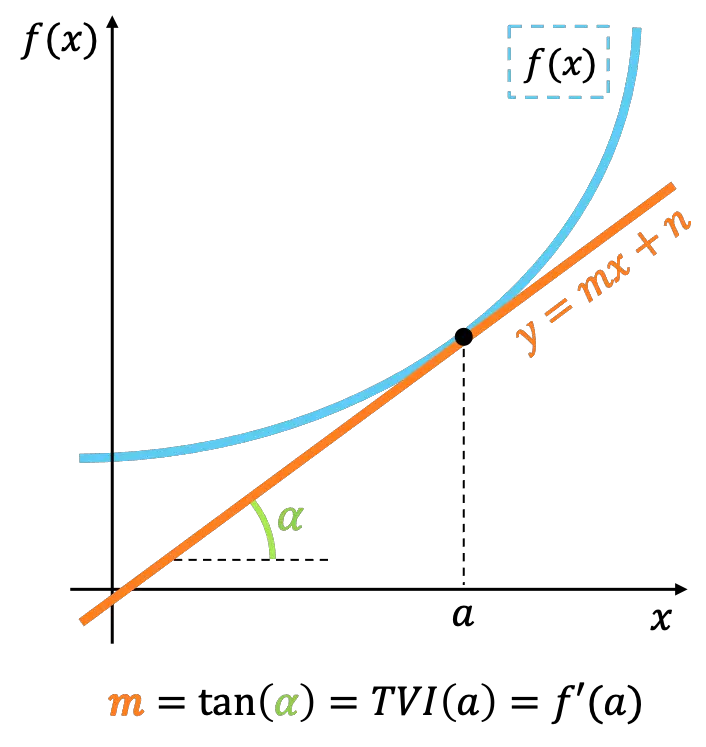
자세히 보면 순간변화율의 의미는 함수의 미분 개념 과 동일하다. 따라서 순간 변화율은 한 지점에서 함수의 도함수 값을 계산하는 데에도 사용됩니다.

변화율에 대한 해결 연습

연습 1

구간 [1,3]에서 다음 함수의 변화율 값을 계산합니다.

$f(x)=x^2-5$

솔루션 보기

먼저 구간 끝에서 함수의 값을 결정합니다.

$f(1)=1^2-5=1-5=-4$

$f(3)=3^2-5=9-5=4$

이제 변화율 공식을 적용합니다.

$\text{TV}[a,b]=f(b)-f(a)$

$\text{TV}[1,3]=f(3)-f(1)=4-(-4)=4+4=\bm{8}$

연습 2

구간 [1,4]에 걸쳐 다음 함수의 평균 변화율(TVM)을 계산합니다.

$f(x)=2x+1$

솔루션 보기

먼저 x=1과 x=4에서 함수의 이미지를 계산합니다.

$f(4)=2\cdot4+1=9$

$f(1)=2\cdot 1+1=3$

그리고 평균 변화율에 대한 공식을 적용합니다.

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [1,4] = \cfrac{f(4)-f(1)}{4-1} = \cfrac{9-3}{4-1}=\cfrac{6}{3} = \bm{2}$

연습 3

구간 [-1.3]에서 다음 함수의 평균 변화율을 구합니다.

$f(x)=(x+1)^2$

솔루션 보기

평균 변화율을 결정하려면 먼저 f(-1)과 f(3)을 계산해야 합니다.

$f(3)=(3+1)^2=(4)^2=16$

$f(-1)=((-1)+1)^2=(0)^2=0$

이제 평균 변화율에 대한 공식을 사용합니다.

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [-1,3] = \cfrac{f(3)-f(-1)}{3-(-1)} = \cfrac{16-0}{3+1}=\cfrac{16}{4} = \bm{4}$

연습 4

다음 그래프에 표시된 함수의 간격 [2,4]에서 평균 변화율을 계산합니다.

솔루션 보기

평균 변화율에 대한 공식을 적용합니다.

$\text{TVM} [a,b] = \cfrac{f(b)-f(a)}{b-a}$

$\text{TVM} [2,4]=\cfrac{f(4)-f(2)}{4-2}$

공식에서 볼 수 있듯이 f(4)와 f(2)의 값을 찾아야 합니다. 이는 함수의 그래픽 표현을 보면 쉽게 수행할 수 있습니다.

$f(4)=5$

$f(2)=1$

이제 함수의 값을 알았으므로 이를 공식으로 대체합니다.

$\text{TVM}[2,4]=\cfrac{f(4)-f(2)}{4-2}=\cfrac{5-1}{4-2}=\cfrac{4}{2}=\bm{2}$

연습 5

x=2 지점에서 다음 함수의 순간 변화율을 계산합니다.

$f(x)=3x$

솔루션 보기

x=2 지점에서 함수의 순간 변화율을 결정하기 위해 해당 공식을 적용합니다.

$\text{TVI}(a)=\lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\begin{array}{l}\text{TVI}(2)=\lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{3(2+h)-3\cdot 2}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{6+3h-6}{h}= \lim\limits_{h \to 0} \cfrac{3h}{h} =\\[4ex]=\lim\limits_{h \to 0} \cfrac{3\cancel{h}}{\cancel{h}}=\lim\limits_{h \to 0} 3 = \bm{3}\end{array}$

연습 6

x=1 지점에서 다음 함수의 순간 변화율(TVI)을 결정합니다.

$f(x)=x^2+1$

솔루션 보기

순간 변화율에 대한 공식을 적용합니다.

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}$

그런 다음 계산합니다.

$f(1+h)$

그리고

$f(1):$

$f(1+h) = (1+h)^2+1$

$f(1)=1^2+1=1+1=2$

그리고 한계에 있는 값을 다음과 같이 대체합니다.

$\text{TVI} (1) = \lim\limits_{h \to 0} \cfrac{f(1+h)-f(1)}{h}= \lim\limits_{h \to 0} \cfrac{(1+h)^2+1-2}{h} =\lim\limits_{h \to 0} \cfrac{(1+h)^2-1}{h}$

우리는 주목할만한 제품을 해결합니다:

$\lim\limits_{h \to 0} \cfrac{1^2+h^2+2\cdot 1 \cdot h-1}{h}=\lim\limits_{h \to 0} \cfrac{1+h^2+2h-1}{h}=\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}$

이제 한계를 해결해 보겠습니다.

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\cfrac{0^2+2\cdot 0}{0} = \cfrac{0}{0}$

그러나 우리는 0을 0으로 나눈 불확정 형식을 찾았으므로 분수 분자의 다항식을 인수분해하고 단순화합니다.

$\lim\limits_{h \to 0} \cfrac{h^2+2h}{h}=\lim\limits_{h \to 0} \cfrac{h(h+2)}{h} = \lim\limits_{h \to 0} \cfrac{\cancel{h}(h+2)}{\cancel{h}}= \lim\limits_{h \to 0}(h+2)$

➤ 0 사이의 0 불확정성을 해결하는 방법을 모른다면 위 링크에서 0 사이의 0 불확정성이 있는 극한을 해결하는 방법에 대한 전체 설명을 볼 수 있습니다.

마지막으로 한계를 해결합니다.

$\lim\limits_{h \to 0}(h+2) = 0+2 =\bm{2}$

요약하면, x=1 지점에서 함수의 순간 변화율은 2와 같습니다.

$\mathbf{TVI} \bm{(1) = 2}$

연습 7

x=2 지점에서 다음 함수의 순간 변화율을 구합니다.

$f(x)=4x^2-x+3$

솔루션 보기

먼저 순간 변화율 공식을 사용합니다.

$\text{TVI} (a) = \lim\limits_{h \to 0} \cfrac{f(a+h)-f(a)}{h}$

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}$

우리는 계산한다

$f(2+h)$

그리고

$f(2):$

$f(2+h) = 4(2+h)^2-(2+h)+3=4(2+h)^2-h+1$

$f(2) =4\cdot 2^2-2+3=4\cdot 4-2+3 =17$

그리고 한계에 있는 값을 다음과 같이 대체합니다.

$\text{TVI} (2) = \lim\limits_{h \to 0} \cfrac{f(2+h)-f(2)}{h}=\\[4ex]=\lim\limits_{h \to 0} \cfrac{4(2+h)^2-h+1-17}{h}=\\[4ex]= \lim\limits_{h \to 0} \cfrac{4(2+h)^2-h-16}{h}$

우리는 주목할만한 평등을 계산합니다.

$\lim\limits_{h \to 0} \cfrac{4(2^2+h^2+2\cdot 2 \cdot h)-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4(4+h^2+4h)-h-16}{h}$

우리는 분자에 대해 작업합니다:

$\lim\limits_{h \to 0} \cfrac{16+4h^2+16h-h-16}{h}=\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}$

이제 한계를 해결해 보겠습니다.

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\cfrac{4\cdot0^2+15\cdot 0}{0} = \cfrac{0}{0}$

그러나 우리는 불확정성 0을 0으로 나누어서 다항식을 인수분해하고 단순화합니다.

$\lim\limits_{h \to 0} \cfrac{4h^2+15h}{h}=\lim\limits_{h \to 0} \cfrac{h(4h+15)}{h}=\lim\limits_{h \to 0} \cfrac{\cancel{h}(4h+15)}{\cancel{h}}= \lim\limits_{h \to 0}(4h+15)$

마지막으로 한계를 해결합니다.

$\lim\limits_{h \to 0}(4h+15)=4\cdot 0+15 =\bm{15}$

아직:

$\mathbf{TVI} \bm{(2) = 15}$

변화율은 얼마입니까?

평균 변화율

함수의 평균 변화율을 계산하는 예

평균 변화율의 기하학적 해석

순간 변화율

함수의 순간 변화율 계산 예

순간변화율의 기하학적 해석

변화율에 대한 해결 연습

연습 1

연습 2

연습 3

연습 4

연습 5

연습 6

연습 7

댓글 달기 댓글 취소