여기서 탄젠트 함수가 어떻게 파생되는지 알아보세요. 또한 탄젠트의 미분 예를 볼 수 있으며 단계별로 풀어보는 연습 문제를 통해 연습할 수도 있습니다. 마지막으로 탄젠트 미분 공식을 시연하고 역탄젠트 미분 공식도 보여줍니다.
탄젠트의 미분은 무엇입니까?
x 탄젠트의 도함수는 x 코사인의 제곱에 대한 1과 같습니다. x의 탄젠트의 도함수는 x의 시컨트의 제곱과 1에 x의 탄젠트의 제곱을 더한 것과 동일합니다.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dfb81626a982a908c4e517b1ecb748e7_l3.png)
모든 표현식은 동일하므로 탄젠트 함수에는 이를 파생하는 세 가지 공식이 있습니다.
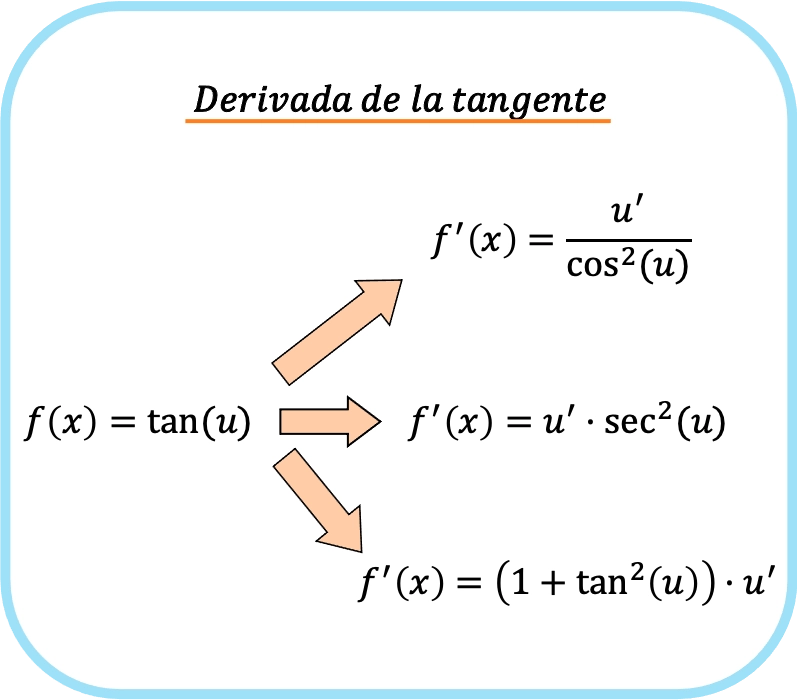
반면에 접선 인수에 x와 다른 함수(u라고 부르자)가 있는 경우 체인 규칙을 적용해야 합니다. 따라서 u의 탄젠트의 미분은 다음과 같습니다.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1ad272ab857ecf57ebc79e68a4370fc5_l3.png)
즉, 탄젠트 미분 규칙은 다음과 같이 요약될 수 있습니다.
탄젠트 도함수의 예
탄젠트 도함수에 대한 공식이 주어지면 이 섹션에서는 탄젠트 함수를 유도하는 방법을 이해할 수 있도록 이러한 유형의 삼각 도함수에 대한 몇 가지 예를 풀 것입니다.
예 1: 2x 탄젠트의 미분
![]()
탄젠트의 미분을 계산하려면 위에서 본 세 가지 공식 중 하나를 사용할 수 있습니다. 이 경우 코사인 공식을 사용합니다.
![]()
함수 2x는 선형이므로 그 도함수는 2입니다. 따라서 2x 탄젠트의 도함수는 2x 코사인의 제곱에 대한 2입니다.
![]()
예 2: x 제곱의 탄젠트 파생
![]()
이 예에서 탄젠트 인수 함수는 x가 아니라 도함수가 있는 함수입니다. 즉, 이를 도출하려면 체인 규칙을 적용해야 합니다.
![]()
x 제곱의 도함수는 2x이므로 x 2 탄젠트의 도함수는 다음과 같습니다.
![]()
예 3: 입방체에 대한 접선의 미분
![]()
이 문제에는 복합 함수가 있으므로 접선을 구별하기 위해 체인 규칙을 사용해야 합니다.
![]()
또한 탄젠트가 3의 거듭제곱으로 증가합니다. 즉, 탄젠트 도함수 공식을 적용하기 전에 거듭제곱 도함수 공식을 사용해야 합니다.
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-424a7372a1d97a5c17a86d6253666164_l3.png)
역탄젠트의 미분
다른 역함수와 마찬가지로 탄젠트 함수에도 역탄젠트 함수인 아크탄젠트 함수가 있습니다. 이를 도출하는 공식은 접선 공식과 유사하지 않지만 경우에 따라 유용할 수 있으므로 보여드립니다.
함수 의 역탄젠트의 도함수는 함수의 도함수를 1로 나눈 값과 해당 함수의 제곱을 더한 값의 몫입니다.
![]()
예를 들어, 3x의 역탄젠트의 미분은 다음과 같습니다.
![]()
접선의 미분에 대한 해결 연습
다음 접선 함수의 미분을 계산합니다.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
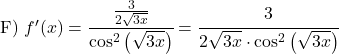
탄젠트의 미분 증명
이것이 꾸며낸 표현이 아니라는 것을 확인할 수 있도록, 이 섹션에서는 탄젠트의 수학적 정의를 사용하여 탄젠트 도함수 공식을 보여드리겠습니다.
이를 위해 세 가지 삼각비를 연결하는 삼각 항등식부터 시작하겠습니다.
![]()
나눗셈의 미분 공식을 사용하면 미분은 다음과 같습니다.
![]()
![]()
![]()
그러나 기본적인 삼각법 항등식을 사용하면 사인의 제곱과 코사인의 제곱의 합이 1이라는 것을 알 수 있습니다.
![]()
![]()
그래서 우리는 이미 접선의 미분에 대한 첫 번째 공식에 도달했습니다. 더욱이 시컨트는 코사인의 곱셈의 역이므로 두 번째 표현도 파생됩니다.
![]()
마지막으로, 접선 도함수의 세 번째 규칙은 이전 단계의 분수를 분수의 합으로 변환하여 증명할 수 있습니다.
![]()
![]()
![]()