크레이머의 법칙 - 마토리티(Mathority)

이 페이지에서는 Cramer의 법칙이 무엇인지 확인하고 Cramer의 법칙에 따라 방정식 시스템을 푸는 예제와 연습을 찾을 수 있습니다.

크레이머의 법칙은 무엇인가?

크래머의 법칙(Cramer’s rule)은 행렬식을 사용하여 연립방정식을 푸는 데 사용되는 방법입니다. 그것이 어떻게 사용되는지 봅시다:

방정식 시스템을 고려하십시오.

$\begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}$

시스템의 행렬 A와 확장 행렬 A’는 다음과 같습니다.

$\displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)$

크레이머의 법칙 에 따르면 연립방정식의 해는 다음과 같습니다.

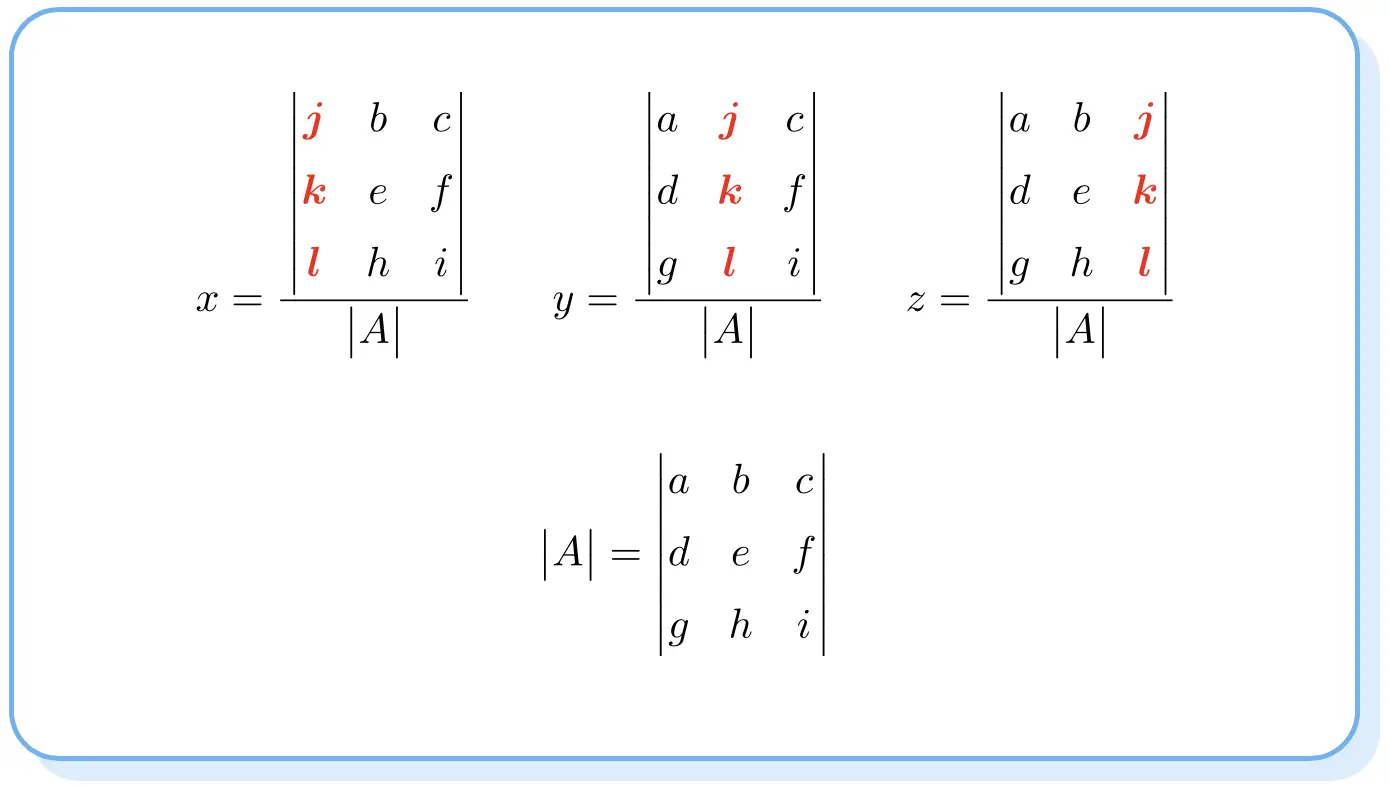
분자의 행렬식은 행렬 A의 행렬식과 비슷하지만 각 미지수의 열을 독립 항의 열로 변경한다는 점에 유의하세요.

따라서 Cramer의 법칙은 선형 방정식 시스템을 해결하는 데 사용됩니다. 그러나 이미 알고 있듯이 연립방정식을 푸는 방법에는 여러 가지가 있습니다. 예를 들어 Gauss Jordan의 방법은 잘 알려져 있습니다.

다음은 Cramer의 법칙을 사용하거나 때때로 Kramer의 법칙으로 작성된 선형 방정식 시스템의 해를 구하는 예입니다.

예시 1: 결정된 호환 시스템(SCD)

Cramer의 법칙을 사용하여 3개의 미지수가 있는 다음 3개 방정식 시스템을 풉니다.

$\begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}$

먼저 시스템의 행렬 A와 확장 행렬 A’를 만듭니다.

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)$

이제 어떤 유형의 시스템인지 확인하기 위해 두 행렬의 순위를 계산합니다. A의 순위를 계산하기 위해 전체 행렬의 3×3 행렬식을 계산하고(Sarrus의 규칙을 사용하여) 0이 나오는지 확인합니다.

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0$

A의 행렬식은 0과 다르므로 행렬 A의 순위는 3입니다.

$\displaystyle rg(A)=3$

따라서 행렬 A’도 랭크 3입니다 . 이는 랭크 4일 수 없고 최소한 행렬 A와 동일한 랭크여야 하기 때문입니다.

$\displaystyle rg(A')=3$

행렬 A의 범위는 행렬 A’의 범위 및 시스템의 미지수 수(3)와 동일합니다. 따라서 Rouché-Frobenius 정리 에 의해 우리는 이것이 결정된 호환 시스템 (SCD)임을 알 수 있습니다.

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

시스템이 SCD라는 것을 알게 되면 이를 해결하기 위해 Cramer의 규칙을 적용합니다. 이를 수행하려면 행렬 A, 행렬식 및 행렬 A’가 다음과 같다는 점을 기억하십시오.

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24$

미지수를 계산하려면

$\displaystyle x$

Cramer의 법칙을 사용하여 A의 행렬식의 첫 번째 열을 독립 항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}$

미지수를 계산하려면

$\displaystyle y$

크래머의 법칙을 사용하여 A 행렬식의 두 번째 열을 독립항 열로 변경하고 이를 A 행렬식으로 나눕니다.

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}$

계산하다

$\displaystyle z$

Cramer의 법칙을 사용하여 A의 행렬식의 세 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}$

따라서 연립방정식의 해는 다음과 같습니다.

$\displaystyle \bm{x = 1 \qquad y=2 \qquad z = -1}$

예 2: 불확실한 호환 시스템(ICS)

Cramer의 법칙을 사용하여 다음 방정식 시스템을 풉니다.

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}$

먼저 시스템의 행렬 A와 확장 행렬 A’를 만듭니다.

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)$

이제 두 행렬의 범위를 계산하여 그것이 어떤 유형의 시스템인지 확인할 수 있습니다. A의 순위를 계산하기 위해 전체 행렬의 행렬식을 계산하고(Sarrus의 규칙을 사용하여) 0인지 확인합니다.

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0$

행렬식은 0을 제공하므로 행렬 A는 순위 3이 아닙니다. 그러나 행렬식은 0과 다른 2×2 행렬식을 갖습니다.

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

따라서 행렬 A의 순위는 2입니다 .

$\displaystyle rg(A)=2$

행렬 A의 범위를 알고 나면 행렬 A’의 범위를 계산합니다. 처음 3개 열의 행렬식은 0을 제공하므로 행렬 A’에서 다른 가능한 3×3 행렬식을 시도해 봅니다.

$\displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0$

3차의 모든 행렬식은 0을 제공합니다. 그러나 분명히 행렬 A’는 행렬 A와 동일한 0이 아닌 2×2 행렬식을 갖습니다.

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

따라서 행렬 A’도 랭크 2입니다 .

$\displaystyle rg(A')=2$

따라서 행렬 A의 순위는 행렬 A’의 순위와 동일하지만 이 둘은 시스템(3)의 미지수 수보다 작기 때문에 Rouché-Frobenius 정리 에 의해 이것이 불확정적으로 호환 가능한 시스템 이라는 것을 알 수 있습니다. (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

호환 가능한 불확정 시스템(SCI)을 풀려면 시스템을 변환해야 합니다. 먼저 방정식을 제거한 다음 변수를 λ(일반적으로 변수 z)로 변환하고 마지막으로 λ가 있는 항을 다음과 함께 넣습니다. 독립적인 용어.

시스템을 변환한 후에는 Cramer의 법칙을 적용하고 λ의 함수로 시스템의 해를 얻습니다.

이 경우 시스템에서 마지막 방정식을 제거합니다 .

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}$

이제 변수 z를 λ로 변환해 보겠습니다.

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}$

그리고 우리는 독립된 항을 λ로 갖는 항을 넣습니다.

$\begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}$

따라서 시스템의 행렬 A와 행렬 A’는 다음과 같이 유지됩니다.

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)$

마지막으로 시스템을 변형한 후에 는 Cramer의 법칙을 적용합니다 . 따라서 우리는 A의 행렬식을 푼다:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13$

미지수를 계산하려면

$\displaystyle x$

Cramer의 법칙을 사용하여 A의 행렬식의 첫 번째 열을 독립 항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}$

미지수를 계산하려면

$\displaystyle y$

크래머의 법칙을 사용하여 A 행렬식의 두 번째 열을 독립항 열로 변경하고 이를 A 행렬식으로 나눕니다.

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}$

연립방정식의 해는 λ의 함수이지만 SCI이므로 무한히 많은 해를 갖습니다.

$\displaystyle \bm{x =} \cfrac{\bm{3-14\lambda} }{\bm{13}} \qquad \bm{y=}\cfrac{\bm{2-5\lambda} }{\bm{13}} \qquad \bm{z = \lambda}$

크레이머의 법칙으로 문제 해결

연습 1

Cramer의 법칙을 적용하여 2개의 미지수를 갖는 다음 2개의 방정식 시스템을 풉니다.

해결책 보기

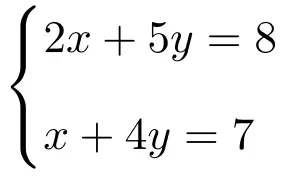
가장 먼저 해야 할 일은 시스템의 행렬 A와 확장 행렬 A’입니다.

$\displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)$

이제 행렬 A의 순위를 찾아야 합니다. 이를 위해 전체 행렬의 행렬식이 0과 다른지 확인합니다.

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}$

행렬은 0과 다른 2×2 행렬식을 가지므로 행렬 A는 순위 2를 갖습니다.

$\displaystyle rg(A)=2$

A의 순위를 알면 A’의 순위를 계산합니다. 이것은 적어도 랭크 2가 될 것입니다. 왜냐하면 우리는 내부에 0과 다른 차수 2의 행렬식이 있다는 것을 보았기 때문입니다. 게다가 3×3 행렬식을 만들 수 없기 때문에 랭크 3이 될 수 없습니다. 따라서 행렬 A’도 랭크 2입니다.

$\displaystyle rg(A')=2$

따라서 Rouché-Frobenius 정리를 적용하면 A의 범위가 A’의 범위 및 미지수의 개수와 동일하므로 이것이 호환 가능한 결정계 (SCD)임을 알 수 있습니다.

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

시스템이 SCD라는 것을 알게 되면 이를 해결하기 위해 Cramer의 규칙을 적용합니다.

미지수를 계산하려면

$\displaystyle x$

Cramer의 법칙을 사용하여 A의 행렬식의 첫 번째 열을 독립 항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}$

미지수를 계산하려면

$\displaystyle y$

크래머의 법칙을 사용하여 A 행렬식의 두 번째 열을 독립항 열로 변경하고 이를 A 행렬식으로 나눕니다.

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}$

따라서 연립방정식의 해는 다음과 같습니다.

$\displaystyle \bm{x = -1 \qquad y=2}$

연습 2

Cramer의 법칙을 사용하여 3개의 미지수가 있는 다음 3개 방정식 시스템의 해를 구합니다.

해결책 보기

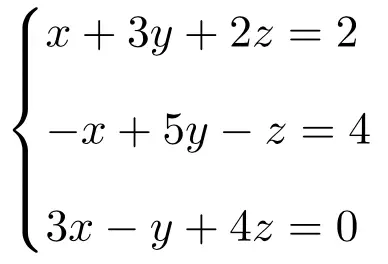
먼저 시스템의 행렬 A와 확장 행렬 A’를 만듭니다.

$\displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)$

이제 Sarrus 규칙을 사용하여 3×3 행렬의 행렬식을 계산하여 행렬 A의 순위를 찾습니다.

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}$

0과 다른 3차 행렬식을 갖는 행렬인 행렬 A는 랭크 3입니다.

$\displaystyle rg(A)=3$

결과적으로 행렬 A’도 랭크 3입니다.

$\displaystyle rg(A')=3$

따라서 Rouché-Frobenius 정리를 사용하면 A의 범위가 A’의 범위 및 미지수의 개수와 동일하므로 이것이 호환 가능한 결정계 (SCD)임을 알 수 있습니다.

시스템이 SCD라는 것을 알게 되면 시스템을 풀기 위해 Cramer의 규칙을 적용해야 합니다.

미지수를 계산하려면

$\displaystyle x$

Cramer의 법칙을 사용하여 A의 행렬식의 첫 번째 열을 독립 항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}$

미지수를 계산하려면

$\displaystyle y$

크래머의 법칙을 사용하여 A 행렬식의 두 번째 열을 독립항 열로 변경하고 이를 A 행렬식으로 나눕니다.

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}$

계산하다

$\displaystyle z$

Cramer의 법칙을 사용하여 A의 행렬식의 세 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}$

따라서 연립방정식의 해는 다음과 같습니다.

$\displaystyle \bm{x =3 \qquad y=1 \qquad z=-2}$

연습 3

Cramer의 법칙을 사용하여 3개의 미지수가 있는 다음 3개 방정식 시스템의 해를 계산합니다.

해결책 보기

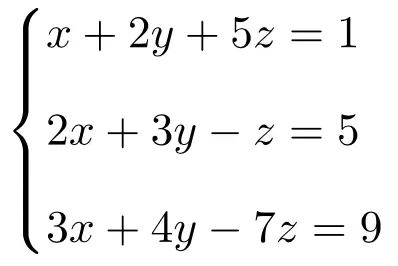
먼저 시스템의 행렬 A와 확장 행렬 A’를 만듭니다.

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)$

행렬 A의 범위를 계산합니다.

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0$

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0$

3차의 모든 행렬식은 0을 제공합니다. 그러나 행렬 A’는 행렬 A와 동일한 2×2 non-0 행렬식을 갖습니다.

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

따라서 행렬 A’도 랭크 2입니다.

$\displaystyle rg(A')=2$

행렬 A의 순위는 행렬 A’의 순위와 동일하지만 이 둘은 시스템(3)의 미지수 수보다 작기 때문에 Rouché-Frobenius 정리를 통해 이것이 불확정 호환 시스템 (ICS)임을 알 수 있습니다.

ICS 시스템이기 때문에 방정식을 제거해야 합니다. 이 경우 시스템에서 마지막 방정식을 제거합니다 .

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}$

이제 변수 z를 λ로 변환해 보겠습니다.

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}$

그리고 우리는 독립된 항을 λ로 갖는 항을 넣습니다.

$\begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}$

시스템의 행렬 A와 행렬 A’는 다음과 같이 유지됩니다.

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)$

마지막으로 시스템을 변형한 후에 는 Cramer의 법칙을 적용합니다 . 따라서 우리는 A의 행렬식을 푼다:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1$

미지수를 계산하려면

$\displaystyle x$

Cramer의 법칙을 사용하여 A의 행렬식의 첫 번째 열을 독립 항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}$

미지수를 계산하려면

$\displaystyle y$

크래머의 법칙을 사용하여 A 행렬식의 두 번째 열을 독립항 열로 변경하고 이를 A 행렬식으로 나눕니다.

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}$

연립방정식의 해는 λ의 함수이지만 SCI이므로 무한히 많은 해를 갖습니다.

$\displaystyle \bm{x =7+17\lambda} \qquad \bm{y=-3-11\lambda} \qquad \bm{z = \lambda}$

연습 4

Cramer의 법칙을 적용하여 3개의 미지수를 갖는 3개 연립방정식의 다음 문제를 해결합니다.

$\begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}$

해결책 보기

먼저 시스템의 행렬 A와 확장 행렬 A’를 구성합니다.

$\displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)$

이제 Sarrus의 규칙을 사용하여 3×3 행렬의 행렬식을 계산하여 행렬 A의 순위를 계산해 보겠습니다.

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}$

0과 다른 3차 행렬식을 갖는 행렬인 행렬 A는 랭크 3입니다.

$\displaystyle rg(A)=3$

결과적으로 행렬 A’도 랭크 3입니다. 왜냐하면 행렬 A’는 적어도 행렬 A와 동일한 랭크여야 하고 3×4 차원의 행렬이기 때문에 랭크 4가 될 수 없기 때문입니다.

$\displaystyle rg(A')=3$

따라서 Rouché-Frobenius 정리를 사용하여 A의 범위가 A’의 범위 및 미지수의 개수와 동일하므로 이것이 확정 호환 시스템 (SCD)임을 추론합니다.

시스템이 SCD라는 것을 알게 되면 시스템을 풀기 위해 Cramer의 규칙을 적용해야 합니다.

미지수를 계산하려면

$\displaystyle x$

Cramer의 법칙을 사용하여 A의 행렬식의 첫 번째 열을 독립 항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}$

미지수를 계산하려면

$\displaystyle y$

크래머의 법칙을 사용하여 A 행렬식의 두 번째 열을 독립항 열로 변경하고 이를 A 행렬식으로 나눕니다.

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}$

계산하다

$\displaystyle z$

Cramer의 법칙을 사용하여 A의 행렬식의 세 번째 열을 독립항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}$

따라서 선형 방정식 시스템의 해는 다음과 같습니다.

$\displaystyle \bm{x =-2 \qquad y=0 \qquad z=4}$

연습 5

Cramer의 법칙을 사용하여 다음 선형 방정식 시스템을 풉니다.

해결책 보기

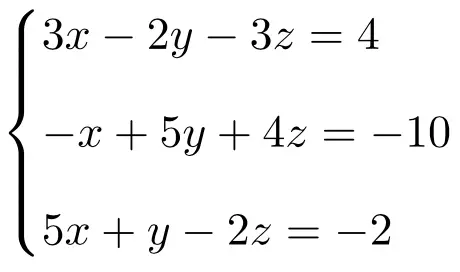
먼저 시스템의 행렬 A와 확장 행렬 A’를 만듭니다.

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)$

행렬 A의 범위를 계산합니다.

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0$

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0$

$\displaystyle rg(A)=2$

$\displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0$

3차 행렬식은 모두 0입니다. 그러나 분명히 행렬 A’는 행렬 A와 마찬가지로 0이 아닌 2차 행렬식과 동일합니다.

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0$

따라서 행렬 A’도 랭크 2입니다.

$\displaystyle rg(A')=2$

행렬 A의 순위는 행렬 A’의 순위와 동일하지만 이 두 개는 시스템의 미지수 수(3)보다 작으므로 Rouché-Frobenius 정리 에 의해 SCI( 불확정 시스템 호환 )임을 알 수 있습니다. :

ICS 시스템이기 때문에 방정식 하나를 제거해야 합니다. 이 경우 시스템에서 마지막 방정식을 제거합니다 .

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}$

이제 변수 z를 λ로 변환해 보겠습니다.

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}$

그리고 우리는 독립된 항을 λ로 갖는 항을 넣습니다.

$\begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}$

시스템의 행렬 A와 행렬 A’는 다음과 같이 유지됩니다.

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)$

마지막으로 시스템을 변형한 후에 는 Cramer의 법칙을 적용합니다 . 따라서 우리는 A의 행렬식을 푼다:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13$

미지수를 계산하려면

$\displaystyle x$

Cramer의 법칙을 사용하여 A의 행렬식의 첫 번째 열을 독립 항의 열로 변경하고 이를 A의 행렬식으로 나눕니다.

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}$

미지수를 계산하려면

$\displaystyle y$

크래머의 법칙을 사용하여 A 행렬식의 두 번째 열을 독립항 열로 변경하고 이를 A 행렬식으로 나눕니다.

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}$

따라서 방정식 시스템의 해는 SCI이므로 시스템에는 무한히 많은 해가 있으므로 λ의 함수입니다.

$\displaystyle \bm{x=} \cfrac{\bm{7\lambda}}{\bm{13}} \qquad \bm{y=} \cfrac{\bm{-26-9\lambda}}{\bm{13}} \qquad \bm{z = \lambda}$

크레이머의 법칙은 무엇인가?

예시 1: 결정된 호환 시스템(SCD)

예 2: 불확실한 호환 시스템(ICS)

크레이머의 법칙으로 문제 해결

연습 1

연습 2

연습 3

연습 4

연습 5

댓글 달기 댓글 취소