이 글에서는 함수(공식)의 코시컨트를 도출하는 방법을 설명합니다. 또한 코시컨트의 도함수에 대해 단계별로 해결되는 연습 문제도 찾을 수 있습니다. 그리고 마지막으로 이러한 유형의 삼각함수 도함수에 대한 공식의 시연을 볼 수 있습니다.
코시컨트 파생 공식
x의 코시컨트의 도함수는 x의 코사인을 x의 제곱 사인으로 나눈 몫을 빼는 것과 같습니다.
![]()
삼각법 공식을 사용하여 x의 코시컨트의 도함수를 x의 코시컨트 곱하기 x의 코시컨트 곱의 마이너스로 정의할 수도 있습니다.
![]()
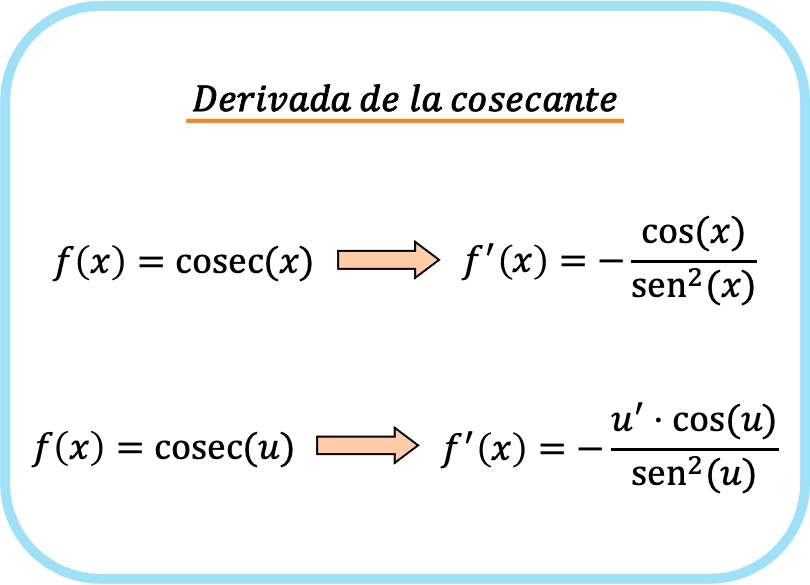
그리고 연쇄 법칙을 적용하면 함수의 코시컨트의 도함수는 함수의 도함수와 함수의 코사인을 곱한 후 함수의 사인 제곱으로 나눈 값을 뺀 값입니다.
![]()
따라서 함수의 코시컨트를 유도하는 데 사용되는 공식은 다음과 같습니다.
코시컨트 도함수의 예
코시컨트의 미분 공식이 무엇인지 살펴보았으므로 이제 몇 가지 예를 들어 보겠습니다. 따라서 함수의 코시컨트가 어떻게 파생되는지 정확히 볼 수 있습니다.
예 1: 2x의 코시컨트 파생
이 예에서 우리는 2x의 코시컨트의 도함수가 얼마나 되는지 볼 것입니다:
![]()
코시컨트 인수 함수는 x와 다르므로 체인 규칙과 함께 코시컨트 미분 규칙을 사용해야 합니다.
![]()
따라서 이 삼각 함수의 도함수를 찾으려면 이전 공식의 값을 간단히 대체하면 됩니다. 코사인 및 사인 인수에 2x를 넣고 u’는 2x의 도함수, 즉 2에 해당합니다.
![]()
예 2: x 제곱의 코시컨트 도함수
이 연습에서는 x 제곱의 코시컨트 도함수가 얼마나 되는지 살펴보겠습니다.
![]()
논리적으로 이 삼각 함수의 도함수는 코시컨트 도함수 공식을 사용하여 해결됩니다.
![]()
x 제곱의 도함수는 2x를 제공하므로 x의 코시컨트의 2제곱 도함수는 다음과 같습니다.
![]()
예 3: 지수 함수의 세제곱 코시컨트 파생
![]()
함수의 인수가 무엇이든, 함수의 코시컨트 도함수에 대한 규칙은 다음과 같습니다.
![]()
그러나 이 경우에는 코시컨트가 3으로 증가하고 더욱이 인수에 지수 함수가 있기 때문에 복합 함수가 있습니다. 따라서 전체 함수를 차별화하려면 체인 규칙을 여러 번 적용해야 합니다.
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ac2ce49dfcba1b7f27696dba0a2decb_l3.png)
코시컨트 도함수 문제 해결
다음 코시컨트 함수를 도출합니다.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-32dde68d2a11ef6a05d483b26f0a98ef_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bea25dae467cefdcc1bd48e8d9bc88_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb70e1d7b6f2ce2636934b235904861f_l3.png)
코시컨트의 도함수에 대한 공식 증명
다음으로 코시컨트의 미분 공식을 설명하겠습니다. 다른 시연과 달리 이 경우 도함수를 정의하는 극한을 사용하지 않고 코시컨트의 수학적 정의부터 시작하겠습니다.
대수학적으로 코시컨트 삼각 함수는 사인의 곱셈의 역수입니다.
![]()
따라서 우리는 몫 규칙을 사용하여 코시컨트의 미분을 취할 수 있습니다.
![]()
![]()
보시다시피, 코시컨트의 도함수에 대한 공식에 도달하는 것은 나눗셈의 도함수에 대한 규칙을 적용함으로써만 가능합니다. 그리고 몫의 도함수는 이미 증명되었으므로(다음 링크에서 볼 수 있음) 코시컨트 도함수 규칙도 증명됩니다.
➤ 참조: 몫의 도함수 증명