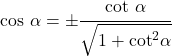코사인 함수

이 페이지에서는 코사인 함수에 대한 모든 것을 찾을 수 있습니다: 코사인 함수가 무엇인지, 공식은 무엇인지, 그래프로 표현하는 방법, 함수의 특성, 진폭, 주기 등. 또한 개념을 완전히 이해하기 위해 코사인 함수의 다양한 예를 볼 수 있습니다. 코사인 정리와 코사인 함수가 다른 삼각비와 갖는 관계도 설명합니다.

코사인 함수 공식

각도 α의 코사인 함수 는 공식이 인접한(또는 인접한) 다리와 직각 삼각형(직각이 있는 삼각형)의 빗변 사이의 비율로 정의되는 삼각 함수입니다.

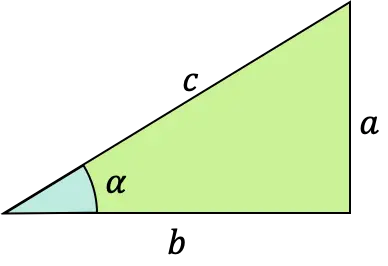
이러한 유형의 수학 함수를 코사인, 코사인 또는 코사인 함수라고도 합니다.

코사인 함수는 각도의 사인 및 탄젠트와 함께 가장 잘 알려진 세 가지 삼각비 중 하나입니다.

코사인 함수의 특성값

일부 각도는 자주 반복되므로 다음 각도에서 코사인 함수의 값을 아는 것이 편리합니다.

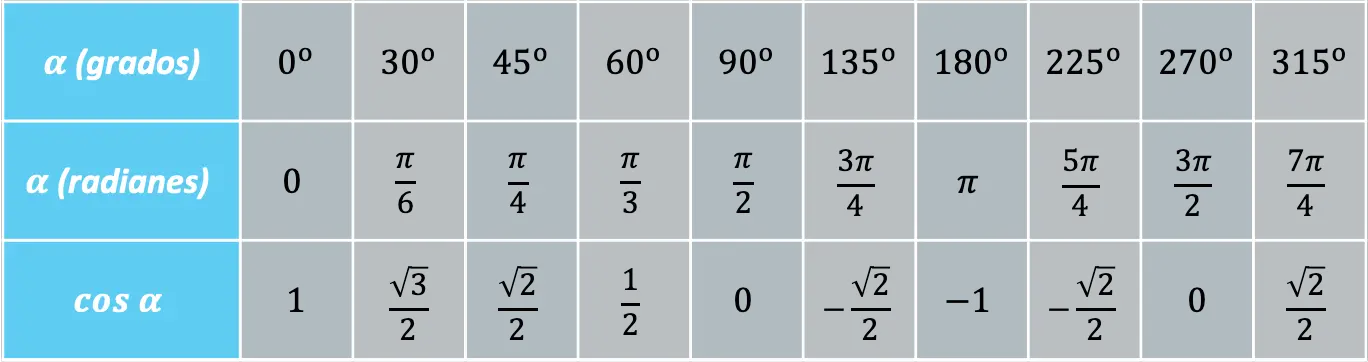
따라서 코사인 함수의 부호는 각도가 위치한 사분면에 따라 달라집니다. 각도가 첫 번째 또는 네 번째 사분면에 있으면 코사인은 양수이고, 각도가 두 번째 또는 세 번째 사분면에 있으면 코사인은 양수입니다. , 코사인은 음수입니다.

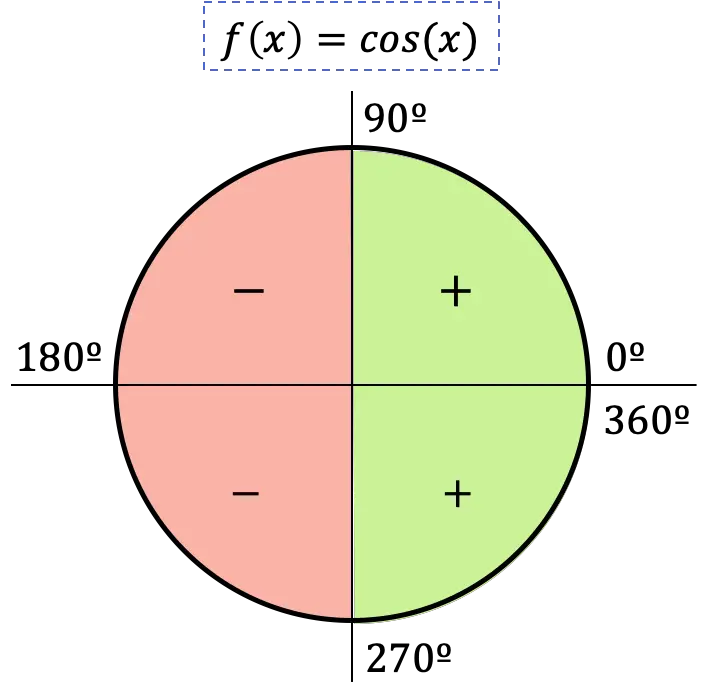
코사인 함수의 그래픽 표현

이전 섹션에서 본 값 표를 사용하여 코사인 함수를 그래프로 표시할 수 있습니다. 그리고 코사인 함수를 그래프로 나타내면 다음을 얻을 수 있습니다.

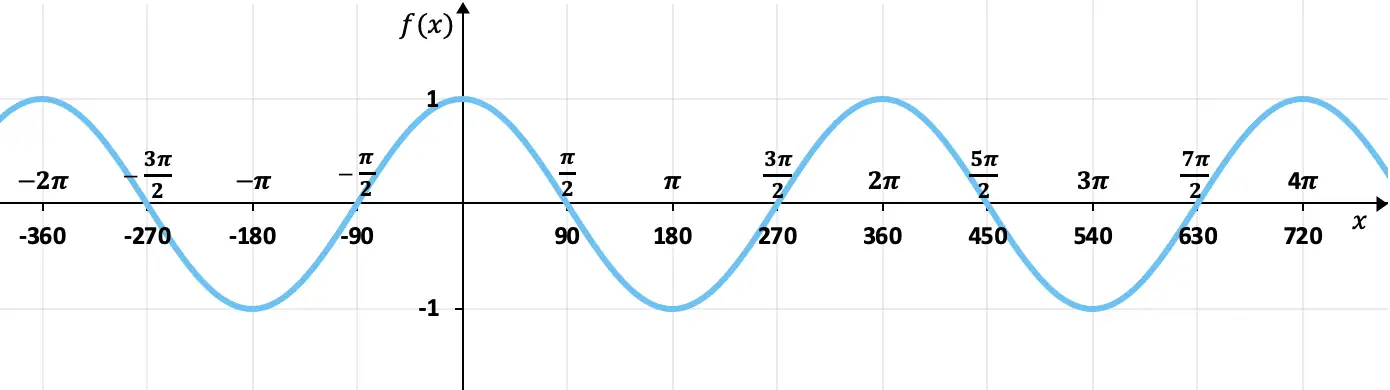
그래프에서 볼 수 있듯이 코사인 함수의 이미지 값은 항상 +1과 -1 사이에 있습니다. 즉, 상단은 +1로 하단은 -1로 제한됩니다. 또한, 그 값은 360도(2π 라디안)마다 반복되므로 주기가 360°인 주기함수 이다.

반면에, 이 그래프에서 우리는 코사인 함수가 짝수라는 것을 완벽하게 인식합니다. 그 반대 요소가 동일한 이미지를 갖기 때문입니다. 즉, 컴퓨터 축(Y축)을 기준으로 대칭입니다. 예를 들어, 90°의 코사인은 0이고 -90°의 코사인은 0입니다.

코사인 함수의 속성

코사인 함수에는 다음과 같은 특징이 있습니다.

코사인 함수의 정의역은 그래프에서 알 수 있듯이 독립 변수 x의 모든 값에 대해 함수가 존재하기 때문에 모두 실수입니다.

$\text{Dom } f = \mathbb{R}$

코사인 함수의 경로 또는 범위는 음수 1부터 양수 1까지(둘 다 포함)입니다.

$\text{Im } f= [-1,1]$

연속함수이고 주기성이 2π인 짝이다.

$\displaystyle \text{cos }x = \text{cos}(-x)$

이 유형의 삼각 함수에는 점 (0,1)에서 OY 축과의 단일 교차점이 있습니다.

$(0,1)$

대신 평균 pi의 홀수 배수 좌표에서 가로좌표(X축)를 주기적으로 가로챕니다.

$\displaystyle \left(\frac{\pi}{2}+k\pi ,0\right) \qquad k \in \mathbb{Z}$

코사인 함수의 최대값은 다음과 같은 경우에 발생합니다.

$x = 2\pi k \qquad k \in \mathbb{Z}$

반대로, 코사인 함수의 최소값은 다음에서 발생합니다.

$x = \pi(2k +1 ) \qquad k \in \mathbb{Z}$

코사인 함수의 미분은 부호가 변경된 사인입니다.

$f(x)=\text{cos } x \ \longrightarrow \ f'(x)= -\text{sen } x$

마지막으로 코사인 함수의 적분은 사인입니다.

$\displaystyle \int \text{cos } x \ dx= \text{sen } x + C$

코사인 함수의 주기와 진폭

그의 그래프에서 보았듯이 코사인 함수는 주기 함수입니다. 즉, 그 값이 주파수와 함께 반복됩니다. 또한 진동하는 최대값과 최소값은 진폭에 따라 달라집니다. 따라서 코사인 함수를 결정하는 두 가지 중요한 특성은 주기와 진폭입니다.

$\displaystyle f(x)= A\text{cos}(wx)$

코사인 함수의 주기는 그래프가 반복되는 두 점 사이의 거리이며 다음 공식으로 계산됩니다.

$\displaystyle \text{Periodo}=T=\cfrac{2\pi}{w}$

코사인 함수의 크기는 코사인 항 앞의 계수와 동일합니다.

$\displaystyle \text{Amplitud}=A$

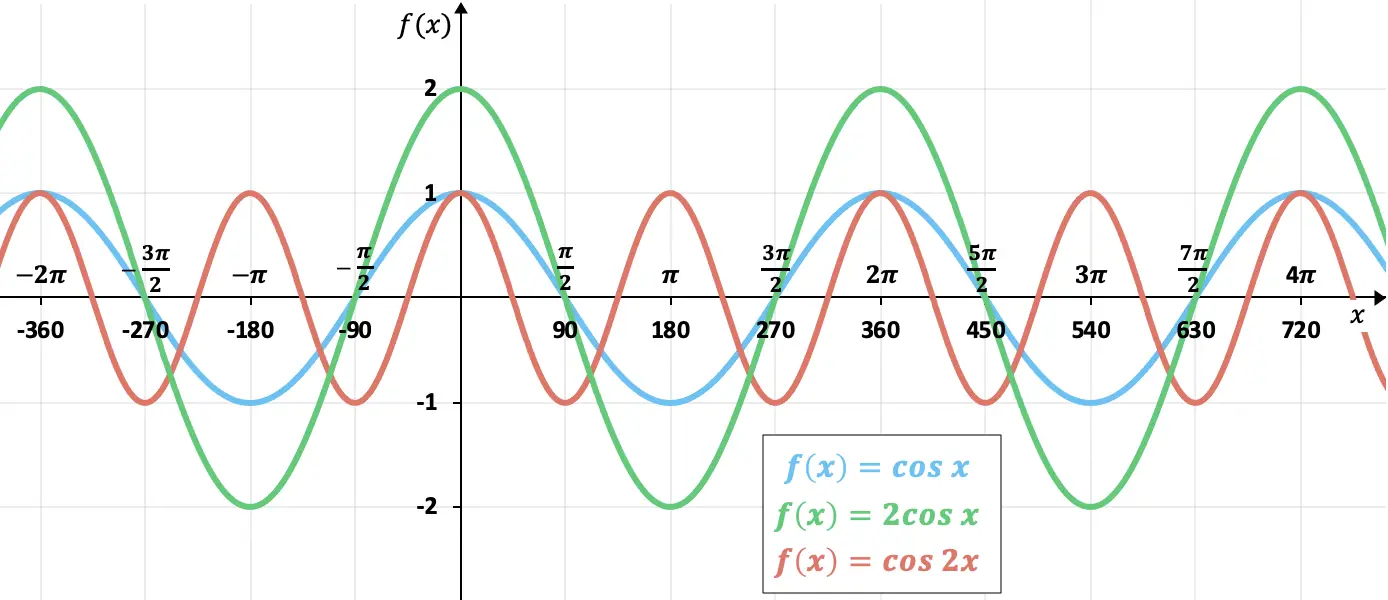
아래에서는 주기 또는 진폭 변경의 효과를 보여주는 그래프를 볼 수 있습니다.

녹색으로 표시된 함수에서 진폭을 두 배로 늘리면 함수가 +1에서 -1이 아닌 +2에서 -2로 바뀌는 것을 볼 수 있습니다. 반면, 빨간색으로 표시된 함수에서는 주기가 절반으로 줄어들었기 때문에 “표준” 코사인 함수보다 두 배 빠르게 진행되는 것을 볼 수 있습니다.

코사인 정리

코사인 공식은 일반적으로 직각 삼각형에 사용되지만 모든 유형의 삼각형에 적용할 수 있는 정리인 코사인 정리 또는 코사인 정리도 있습니다.

코사인 정리는 삼각형의 변과 각도를 다음과 같이 연결합니다.

$a^2=b^2+c^2-2\cdot b \cdot c\cdot \text{cos }\alpha$

$b^2=a^2+c^2-2\cdot a \cdot c\cdot \text{cos }\beta$

$c^2=a^2+b^2-2\cdot a \cdot b\cdot \text{cos }\gamma$

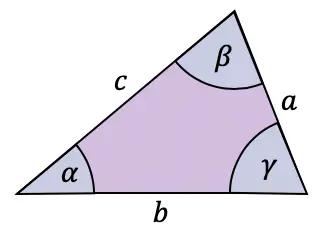
코사인 함수와 다른 삼각비의 관계

그러면 삼각법에서 가장 중요한 삼각비와의 코사인 관계를 얻을 수 있습니다.

유방과의 관계

사인 함수의 그래프는 코사인 곡선과 동일하지만 이동되었습니다.
$\displaystyle \frac{\pi}{2}$

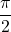
따라서 오른쪽의 두 함수는 다음 표현식으로 연결될 수 있습니다.

$\displaystyle \text{cos }\alpha = \text{sen}\left(\alpha + \frac{\pi}{2} \right)$

사인과 코사인을 삼각법의 기본 항등식과 연관시킬 수도 있습니다.

$\displaystyle \text{sen}^2\alpha + \text{cos}^2\alpha=1$

접선과의 관계

증명하기는 복잡하지만 코사인은 탄젠트에 따라서만 표현할 수 있습니다.

$\displaystyle \text{cos }\alpha = \pm \cfrac{1}{\sqrt{1+\text{tg}^2\alpha \vphantom{\bigl( }}}$

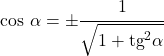
시컨트와의 관계

코사인과 시컨트는 곱셈의 역원입니다.

$\displaystyle \text{cos }\alpha = \cfrac{1}{\text{sec }\alpha}$

코시컨트와의 관계

코사인은 코시컨트에만 의존하도록 풀 수 있습니다.

$\displaystyle \text{cos }\alpha =\pm \cfrac{\sqrt{\text{csc}^2\alpha -1 } }{\text{csc }\alpha}$

코탄젠트와의 관계

각도의 코사인과 코탄젠트는 다음 방정식으로 관련됩니다.

$\displaystyle \text{cos }\alpha =\pm \cfrac{\text{cot }\alpha}{\sqrt{1+\text{cot}^2\alpha \vphantom{\bigl( }}}$