최소 제곱법은 일련의 점에 해당하는 최상의 직선을 찾기 위한 수학적 도구입니다. 우리는 그것을 간단한 방법으로 설명합니다:
여기 저기 흩어져 있는 그래프에 여러 개의 점이 있다고 상상해 보십시오. 선과 점 사이의 거리를 최소화하기 위해 이러한 점에 가장 잘 맞는 직선을 찾고 싶습니다. 이것이 최소제곱법의 기본 아이디어입니다.
이 방법은 공식을 사용하여 점과 선 사이의 차이의 제곱의 합을 최소화하는 선의 방정식을 계산합니다. 즉, 점으로부터 ‘편차’가 가장 작은 선을 찾는 것입니다.
간단히 말해서 최소 제곱법은 조사 중에 얻은 데이터를 분석하는 데 유용하며, 데이터의 동작을 선형 방식으로 표현하고 도난당한 정보의 오류를 줄이는 것을 목표로 합니다.
최소제곱법을 만든 사람은 누구입니까?
통계 및 데이터 분석의 기본 도구인 최소 자승법은 독일 수학자 칼 프리드리히 가우스(Carl Friedrich Gauss) 가 1794년에 제안한 것으로 알려져 있습니다. 그러나 가우스는 1809년 까지 이 방법을 발표하지 않았습니다.
흥미롭게도 프랑스 수학자 앙드리앙-마리 르장드르(Andrien-Marie Legendre)는 1805년에 비슷한 버전을 출판하여 독립적으로 개발했습니다.
두 수학자 모두 관찰된 데이터에 모델을 맞추고 정확한 예측을 하기 위해 다양한 분야에서 널리 사용되는 이 방법을 만드는 데 도움을 주었습니다.
최소제곱 공식
의심할 바 없이 이 방법이 무엇을 포함하는지 이해하려면 공식과 구현 과정을 설명하는 것이 필수적입니다. 최소 제곱 공식에 대한 자세한 설명은 다음과 같습니다.
문제를 정의하다
독립 변수(x)와 종속 변수(y)라는 두 개의 변수가 있는 데이터 세트가 있고 이 데이터에 직선을 맞추려고 한다고 가정해 보겠습니다.
목표는 y의 실제 값과 예측 값 사이의 차이의 제곱의 합을 최소화하는 직선 방정식(절편과 기울기)의 계수 값을 찾는 것입니다. 맞는 라인.
선의 방정식을 계산합니다.
직선 방정식의 형식은 y = mx + b입니다. 여기서 m은 기울기이고 b는 y 절편입니다. myb 값을 계산하기 위한 최소 제곱 공식은 다음과 같습니다.
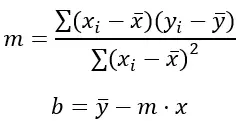
금:
Σ는 값의 합을 나타냅니다.
x i 와 y i 는 각각 각 데이터 포인트에 대한 변수 x와 y의 값입니다.
x̄과 ̳는 각각 x와 y 값의 평균입니다.
(x i – x̄) 및 (y i – )는 x와 y 값과 각각의 평균 간의 차이입니다.
(x i – x̄) 2 는 x 값과 평균 사이의 차이의 제곱입니다.
결과를 해석하다
공식을 사용하여 m과 b의 값을 계산한 후에는 이를 사용하여 적합선의 방정식을 얻을 수 있습니다. 예를 들어 m = 2이고 b = 3인 경우 적합선의 방정식은 y = 2x + 3이 됩니다. 이를 통해 다양한 x 값에 대한 y 값을 예측하거나 추정할 수 있습니다. 조정된 권리를 기준으로 합니다.
최소제곱법은 언제 사용되나요?
아마도 이 방법이 언제 사용되는지 스스로에게 물어볼 것입니다. 다양한 상황에서 매우 유용합니다! 예를 들어, 실험 또는 연구 데이터를 분석하여 관계나 추세를 찾으려 는 경우입니다.
주택 가격과 면적(제곱미터) 사이의 관계를 조사한다고 가정해 보겠습니다. 최소제곱법을 사용하면 데이터에 가장 잘 맞는 직선을 찾을 수 있고 이 관계에 대한 명확한 아이디어를 얻을 수 있습니다.
이는 또한 경제학에서 제품 수요나 가격 행동과 같은 변수를 모델링하고 예측하는 데 사용됩니다. 또한 엔지니어링에서는 수학적 모델을 테스트 또는 시뮬레이션 데이터에 맞추기 위해 최소 제곱법이 적용됩니다.
최소 제곱법은 데이터를 분석하고 중요한 관계를 찾기 위해 다양한 연구 및 작업 분야에서 사용되는 강력하고 다양한 도구입니다.
다른 정리에서 최소제곱법의 응용
최소제곱법은 그 자체로 사용되는 것 외에도 다른 정리에서도 매우 유용합니다. 아래에서 해당 주제에 대해 좀 더 살펴보겠습니다.
회귀 정리
이는 회귀 정리에서 데이터 집합에 가장 적합한 선을 찾는 데 널리 사용됩니다. 예를 들어, 식물의 높이와 받는 빛의 양 사이의 관계를 분석하여 다양한 조명 조건에서 식물이 어떻게 자라는지 판단하는 데 사용할 수 있습니다.
정리 보간
이 경우, 점 집합에 가장 잘 맞는 다항식 함수를 찾기 위해 보간 정리에 최소 제곱법도 적용됩니다. 예를 들어 위치 및 시간 데이터를 기반으로 움직이는 물체의 궤적을 대략적으로 계산하는 데 사용할 수 있습니다.
곡선 피팅 정리
이는 일련의 데이터에 맞는 곡선을 찾기 위해 곡선 피팅 정리에 사용됩니다. 이는 기후 변화를 예측하거나 발사체의 궤적을 예측하기 위한 기후 데이터 모델링과 같은 응용 프로그램에 유용합니다.
푸리에 분석 정리
푸리에 분석 정리에서 최소 제곱법은 일련의 이산 데이터로부터 주기 함수를 근사화하는 데 사용됩니다. 이는 데이터 신호, 이미지 및 사운드 압축에 적용됩니다.
비선형 회귀 정리
마지막으로, 선형 관계를 따르지 않는 데이터 세트에 맞는 최적의 곡선을 찾기 위해 비선형 회귀 정리에 최소 제곱법도 적용됩니다. 예를 들어, 화학물질의 농도가 반응 속도에 어떤 영향을 미치는지 분석하는 데 사용할 수 있습니다.
최소제곱법의 예
최소 제곱법을 적용하는 방법을 더 잘 이해하기 위해 아래 예를 살펴보겠습니다.
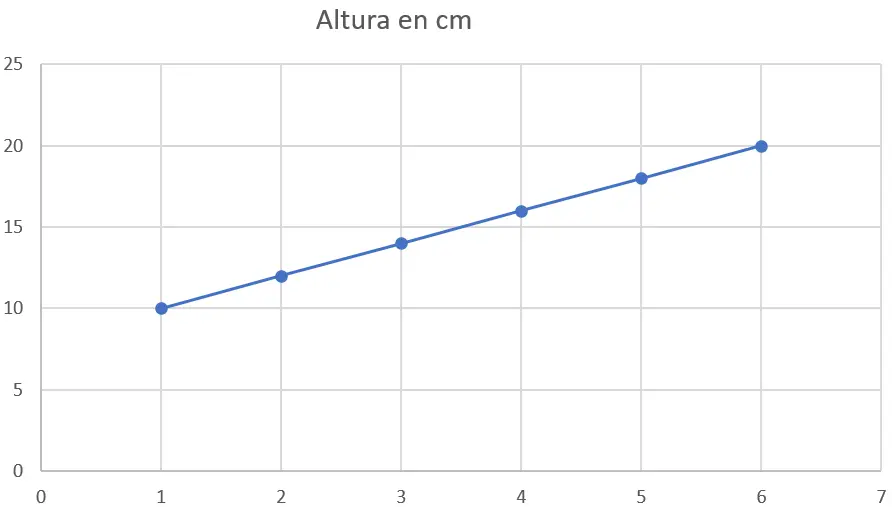
여러 주에 걸쳐 다음과 같은 식물의 높이 데이터(센티미터)가 있다고 가정해 보겠습니다.
| 주 | 높이(센티미터) |
| 1 | 십 |
| 2 | 12 |
| 삼 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | 이십 |
미래의 식물 높이를 예측하기 위해 이 데이터에 가장 적합한 직선을 찾고 싶습니다.
1단계 : 데이터 그래프 작성
가장 먼저 할 일은 산점도에 데이터를 그리는 것입니다. x축은 주를 나타내고 y축은 키를 센티미터 단위로 나타냅니다. 그래프는 다음과 같습니다.
2단계 : 최소제곱법 적용
최소제곱법은 실제 데이터와 선으로 예측한 값의 차이의 제곱의 합을 최소화하는 선을 찾는 방법입니다. 이 경우 선은 선의 방정식으로 표현됩니다: y = mx + b, 여기서 “y”는 높이, “x”는 주, “m”은 선의 기울기, “b”는 y절편.
차이의 제곱합을 최소화하는 “m”과 “b”의 값을 찾으려면 다음 공식을 사용합니다.
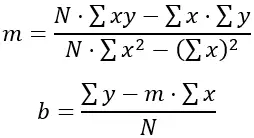
여기서 N은 데이터 포인트 수(이 경우 6), Σxy는 주의 합 x 키, Σx는 주의 합, Σy는 키의 합, Σx 2 는 주의 제곱의 합입니다. .
이러한 공식을 높이 데이터에 적용하면 다음을 얻습니다.
Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630
Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21
Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90
Σx 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 = 91
이 값을 “m”과 “b”의 공식에 대입하면 다음과 같습니다.
m = (6 · 630 – 21 · 90) ¼ (6 · 91 – 21 2 ) ≒ 2.07
b = (90 – 2.07 · 21) ¼ 6 ≒ 3.24
따라서 높이 데이터에 해당하는 직선의 방정식은 y입니다.