평면에서 두 선의 상대적 위치

이 페이지에서는 평면(R2)에서 두 선의 상대적 위치를 결정하기 위해 존재하는 다양한 방법에 대한 설명을 찾을 수 있습니다. 또한, 여러 가지 예를 볼 수 있으며 단계별로 문제를 풀어서 연습할 수 있습니다.

평면에서 두 선의 상대적인 위치는 무엇입니까?

평면에서 두 선 사이의 상대적 위치를 살펴보기 전에 선이 무엇인지 정확히 알아야 합니다. 선 정의 에서 이를 찾을 수 있습니다.

따라서 2차원(R2)에서 작업할 때 두 선 사이에 3가지 유형의 상대 위치가 가능합니다.

교차선

교차하는 두 선의 공통점은 단 하나뿐입니다.

평행선

공통점이 없으면 두 선은 평행합니다. 즉, 그들이 길을 건너지 않는 경우입니다.

일치하는 선

두 선의 점이 모두 공통이면 두 선은 동일합니다.

반면에 평면의 두 선 사이의 각도도 상대적 위치에 따라 달라집니다.

교차선은 0°(포함되지 않음)에서 90°(포함) 사이의 각도로 교차합니다. 또한 두 선이 90° 직각을 이룬다면 두 선이 수직임을 의미합니다.
평행선은 방향이 같으므로 0°의 각도를 이룹니다.
그리고 같은 이유로 일치하는 선들도 그 사이의 각도가 0°가 됩니다.

두 선 사이의 각도가 어떻게 계산되는지 알고 싶다면 두 선 사이의 각도 공식을 확인하세요. 여기에서는 두 선 사이의 각도를 결정하는 방법에 대한 자세한 설명과 몇 가지 예 및 해결된 연습 문제를 찾아 연습하고 개념을 완전히 이해할 수 있습니다.

평면에서 두 선의 상대적 위치를 찾는 방법

2차원 공간에서 두 선 사이의 상대적 위치를 아는 것은 선이 어떻게 표현되는지에 따라 달라집니다.

선 방향 벡터: 두 선의 방향 벡터가 다른 경우 교차해야 합니다. 반면, 방향 벡터의 좌표가 동일하거나 비례하는 경우 평행하거나 일치할 수 있습니다(공통점이 있는지 확인해야 함).

명시적 방정식: 두 직선의 기울기가 다른 경우
$(m)$

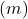
반대로, 선의 기울기는 동일하지만 원점에서의 순서가 다른 경우

$(n)$

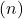
그들은 평행하다. 마지막으로 두 선은 원래 동일한 기울기와 세로 좌표를 갖고 있으면 혼동됩니다.

일반(또는 암시적) 방정식: 비례하지 않는 계수 A와 B를 갖는 두 선은 항상 교차합니다. 그러나 이 두 매개변수가 서로 비례하지만 계수 C에는 비례하지 않을 때 그들은 평행할 것입니다. 그리고 마지막으로 세 항이 비례할 때 이는 선이 혼동된다는 것을 의미합니다.

위 선의 방정식에 대해 의문이 있는 경우 평면의 선 방정식 에 대한 설명을 참조할 수 있습니다. 여기서는 모든 선 방정식의 공식, 계산 방법, 선 방정식의 예제 및 해결 연습을 찾을 수 있습니다.

다음 표에는 이전 속성이 요약되어 있습니다.

다음으로 두 선 사이의 상대적 위치를 결정하는 방법에 대한 두 가지 예를 살펴보겠습니다.

실시예 1

명시적 방정식의 형태로 정의된 다음 두 선 사이의 상대 위치를 찾습니다.

$r: \ y=3x+2 \qquad \qquad s: \ y=3x-4$

두 선의 기울기는 동일합니다.

$m_r = m_s = 3$

그러나 원본에는 다른 컴퓨터가 있습니다.

$n_r =2\neq n_s=-4$

따라서 기울기는 동일하지만 절편이 다르므로 선은 평행합니다 .

실시예 2

암시적(또는 일반) 방정식으로 표현된 다음 두 선 사이의 상대 위치를 결정합니다.

$r: \ 4x+2y-6=0 \qquad \qquad s: \ -2x-y+3=0$

두 선 모두 명시적 방정식으로 표현되므로 계수 중 비례하는 것이 있는지 확인해야 합니다.

$\cfrac{4}{-2}=\cfrac{2}{-1} = \cfrac{-6}{3} = -2$

선의 3항은 비례하므로 선이 일치합니다 .

방정식 시스템을 사용하여 평면에서 두 선의 상대적 위치 결정

두 선 사이의 상대 위치를 아는 또 다른 방법은 선의 방정식으로 구성된 방정식 시스템을 분석하는 것입니다.

시스템에 고유한 솔루션이 있는 경우 선이 교차합니다. 게다가 두 선의 교차점은 시스템의 해이다.
해가 없는 시스템 인 경우 이는 선에 공통점이 없으므로 평행선임을 나타냅니다.
시스템에 무한히 많은 해가 있는 경우 이는 선이 모든 점을 공유하므로 교차하는 선임을 의미합니다.

실시예 3

방정식 시스템을 사용하여 다음 두 선의 상대 위치를 계산합니다.

$r: \ 3x+4y+5=0 \qquad \qquad s: \ 5x+y-3=0$

두 선의 상대적 위치를 찾으려면 두 선으로 구성된 다음 선형 방정식 시스템을 풀어야 합니다.

$\left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\}$

이 경우 대체 방법을 사용하여 시스템을 해결합니다. 따라서 우리는 변수를 분리할 것입니다.

$y$

두 번째 방정식에서 이를 첫 번째 방정식으로 대체합니다.

$\left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\} \begin{array}{l} \\[2ex] \longrightarrow \ y=3-5x \end{array}$

$3x+4(3-5x)+5=0$

$3x+12-20x+5=0$

$3x-20x=-12-5$

$-17x=-17$

$x=\cfrac{-17}{-17} = 1$

그리고 우리가 알려지지 않은 것의 가치가 얼마나 되는지 알게 되면

$x$

우리는 그 값을 찾은 표현식으로 대체합니다.

$y:$

$y=3-5x \ \xrightarrow{x \ = \ 1} \ y = 3 -5\cdot 1$

$y = 3 -5 = -2$

따라서 우리는 두 선으로 구성된 연립방정식의 해를 하나만 얻었으므로 두 선이 교차합니다 . 그리고 그것들이 교차하는 지점이 시스템의 해, 즉 지점이다.

$(1,-2).$

평면에서 두 선의 상대적 위치 문제 해결

연습 1

다음 선이 교차하는지, 평행인지, 일치하는지 확인합니다.

$r: \ 3x-y+4=0 \qquad \qquad s: \ 9x-3y+3=0$

해결책 보기

두 선 모두 암시적(또는 일반) 방정식으로 표현되므로 해당 계수가 비례하는지 확인해야 합니다.

$\cfrac{3}{9}=\cfrac{-1}{-3} \neq \cfrac{4}{3}$

선의 계수 A와 B만이 서로 비례하고 계수 C에는 비례하지 않습니다. 따라서 두 선은 평행합니다 .

연습 2

매개변수 방정식으로 표현된 다음 두 선 사이의 상대 위치를 찾습니다.

$\displaystyle r: \ \begin{cases} x=4-5t \\[2ex] y= 1+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=-2t \\[2ex] y=6+9t \end{cases}$

해결책 보기

우리는 두 선으로 구성된 방정식 시스템을 풀어 상대적인 위치를 찾을 수 있습니다. 그러나 매개변수 방정식 형태이기 때문에 방향 벡터를 쉽게 찾을 수 있고, 비례하지 않으면 선이 교차한다는 뜻이다. 그리고 이 경우 우리는 전체 방정식 시스템을 푸는 데 많은 시간을 소비하지 않을 것입니다.

각 선의 방향 벡터의 데카르트 좌표가 매개변수 앞의 숫자가 되도록

$t:$