이 기사에서는 함수의 단조성을 아는 방법, 즉 함수의 증가 및 감소 간격을 찾는 방법을 설명합니다. 또한 기능의 성장과 쇠퇴에 대한 단계별 연습을 통해 연습할 수도 있습니다.
함수의 단조성은 무엇입니까?
함수는 주어진 순서를 유지하는 경우 구간에서 단조롭습니다. 단조로움에는 다섯 가지 유형이 있습니다.
- 단조 증가 함수: 한 지점의 함수 값이 항상 이전 지점의 함수 값보다 크거나 같을 때.
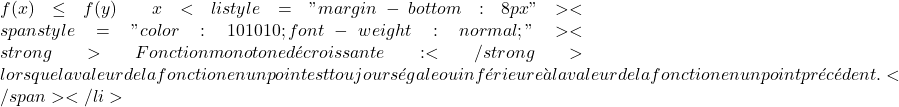엄격 단조 증가 함수: 한 지점의 함수 값이 항상 이전 지점의 함수 값보다 큰 경우.
한 지점의 함수 값이 항상 이전 지점의 함수 값과 같을 때 상수 함수 입니다.
x^2-4=0x^2=4x=\pm 2
\text{Dom } f= \mathbb{R}-\{+2, -2 \}
f(x)=\cfrac{3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-4) – 3\cdot 2x}{\left( x^2-4\right)^2}f'(x)=\cfrac{-6x}{\left(x^2-4\right)^2}
f'(x)=0\cfrac{-6x}{\left(x^2-4\right)^2}=0
\왼쪽(x^2-4\오른쪽)^2}
-6x=0\cdot \left(x^2-4\right)^2-6x=0x=\cfrac{0}{-6}x=0
f'(x)=0,
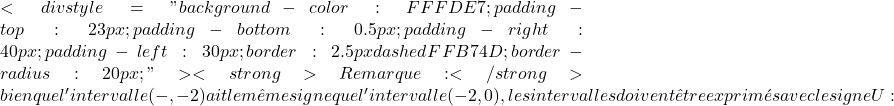
(-\infty,0)
f'(x)=0.
f(x)=x^3-6x^2+9x \ \longrightarrow \ f'(x)=3x^2-12x+9
f'(x)= 03x^2-12x+9=0\begin{정렬됨}x &=\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} = \cfrac{-(- 12) \pm \sqrt{(-12)^2-4\cdot 3 \cdot 9}}{2\cdot 3}=\\[2ex]&= \cfrac{+12 \pm \sqrt{144-108 }}{6} =\cfrac{12 \pm 6}{6}=\begin{사례} \cfrac{12 + 6}{6}= 3 \\[4ex] \cfrac{12 – 6}{6} =1 \end{사례} \end{정렬됨}
f'(x)=0
\text{Dom } f= \mathbb{R}-\{+3, -3 \}
f(x)=\cfrac{5}{x^2-9} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-9) – 5\cdot (2x)}{\ 왼쪽(x^2-9\right)^2}f'(x)= \cfrac{-10x}{\left(x^2-9\right)^2}
f'(x)= 0\cfrac{-10x}{\left(x^2-9\right)^2}=0 -10x=0\cdot \left(x^2-9\right)^2 – 10x= 0 x= \cfrac{0}{-10} x=0
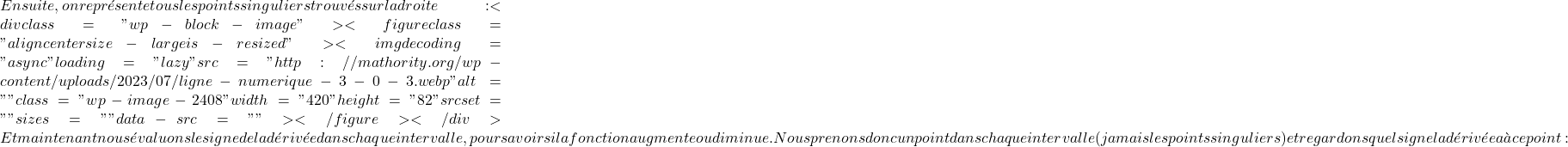
f(x)=\ln \bigl(x^2+1 \bigr) \ \longrightarrow \ f'(x)=\cfrac{1}{x^2+1 } \cdot (2x)f'(x) = \cfrac{2x}{x^2+1}
f'(x)= 0\cfrac{2x}{x^2+1}=0 2x=0\cdot \left(x^2+1\right) 2x= 0 x= \cfrac{0}{2} x=0
