이 기사에서는 직접 비례 함수가 무엇인지, 공식이 무엇인지, 그래프로 표현하는 방법, 주어진 지점에서 방정식을 계산하는 방법을 설명합니다.
직접 비례 함수란 무엇입니까?
직접 비례 함수는 두 개의 정비례 수량을 연결하는 함수입니다. 따라서 종속변수(y)의 값을 계산하려면 종속변수(x)의 값에 비례상수를 곱해야 합니다.
직접 비례 함수는 선형 함수라고도 합니다.
한 수량의 가치가 증가하고 다른 수량도 증가하며 그 반대의 경우에도 두 수량은 정비례한다는 점을 기억하십시오.
정비례 함수의 공식
직접 비례 함수를 정의하는 공식은 다음과 같습니다.
![]()
여기서 y는 독립 변수, x는 종속 변수, ym은 함수의 기울기 또는 비례 상수입니다.
보시다시피, 이 공식을 사용하면 크기 y의 값을 계산하는 것이 매우 쉽습니다. 크기 x의 값에 각 직접 비례 함수의 특성인 함수의 기울기를 곱하면 됩니다.
예를 들어 다음과 같은 직접 비례 함수가 있다고 가정합니다.
![]()
x가 5일 때 y의 양이 얼마인지 확인하려면 함수 (3)의 기울기에 5를 곱하기만 하면 됩니다.
![]()
정비례 함수의 그래픽 표현
다음으로 정비례함수 그래프를 그리는 방법을 알아보겠습니다. 예를 들어 다음 연습을 수행하겠습니다.
![]()
정비례함수를 그래프로 나타내기 위해서는 좌표의 원점 (점 (0,0))을 지나고 함수의 기울기를 갖는 선을 그리면 됩니다.
이 경우 우리가 표현하려는 함수의 기울기는 다음과 같습니다.
![]()
따라서 선은 x 단위마다 y 단위씩 증가해야 합니다.
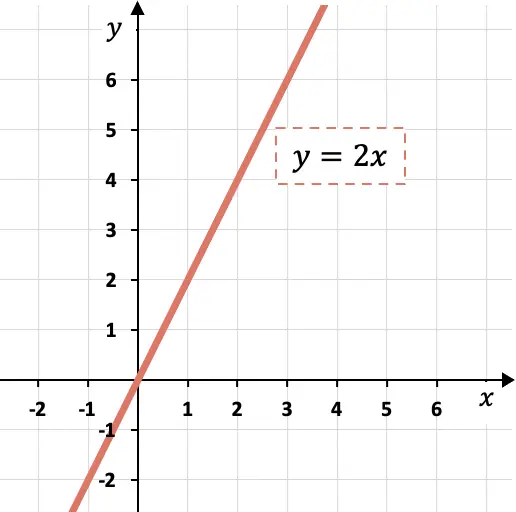
그래프에서 볼 수 있듯이 기울기가 2이면 y 크기가 x 크기의 두 배만큼 증가한다는 의미입니다.
직접 비례 함수는 아핀 함수와 매우 유사한 그래프를 갖지만 두 가지 다른 유형의 함수입니다. 다음 링크에서 아핀 함수와 선형 함수의 차이점을 확인할 수 있습니다.
➤ 참조: 선형 함수와 아핀 함수의 차이점
정비례 함수를 찾는 방법
정비례함수의 한 점을 알면 그 방정식을 쉽게 찾을 수 있습니다. 직접 비례 함수 문제를 해결하여 이것이 어떻게 수행되는지 살펴보겠습니다.
- 화가가 칠하는 방의 수는 대략 그가 일하는 시간에 정비례합니다. 즉, 그가 일하는 시간이 많을수록 그가 칠할 수 있는 방의 수는 더 많아집니다. 그가 하루 8시간 동안 두 개의 방 전체를 칠했다는 것을 안다면 칠해진 방 수와 작업 시간을 연관시키는 정비례 함수는 무엇입니까?
먼저, 어느 것이 종속변수이고 어느 것이 독립변수인지를 결정해야 합니다. 칠해진 조각의 수는 작업한 시간에 따라 달라지며 그 반대는 아닙니다. 따라서 독립변수(x)는 작업한 시간이고 종속변수(y)는 페인트 칠한 방의 수입니다.
문제는 화가가 8시간 안에 방 2개를 칠할 수 있으므로 함수 그래프가 점 (8,2)를 통과해야 한다는 것을 알려줍니다.
![]()
또한 이 명령문은 두 양이 정비례 관계를 가지고 있음을 나타냅니다. 즉, 정비례 함수 공식과 수학적으로 관련되어 있음을 의미합니다.
![]()
이제 점 (8,2)의 좌표를 방정식에 대입하여 함수의 기울기 값을 계산할 수 있습니다.
![]()
그리고 마지막으로 방정식의 알려지지 않은 m을 풉니다.
![]()
![]()
![]()
간단히 말해서, 문제의 정비례 함수는 다음과 같습니다.
![]()
당신은 또한 다음을 좋아할 수도 있습니다:
- 역비례 함수
- 상수 함수