탄젠트 함수

이 페이지에서는 탄젠트 함수에 대한 모든 것을 찾을 수 있습니다: 탄젠트 함수가 무엇인지, 공식은 무엇인지, 그래프로 표현하는 방법, 함수의 특성, 기간 등. 또한 개념을 완전히 이해하기 위해 접선 함수의 예를 볼 수 있습니다. 그는 심지어 접선 정리와 접선 함수가 다른 삼각법 관계와 갖는 관계에 대해서도 설명합니다.

탄젠트 함수 공식

각도 α의 접선 함수는 공식이 직각 삼각형(직각이 있는 삼각형)의 반대 가지와 인접한(또는 인접한) 가지 사이의 비율로 정의되는 삼각 함수입니다.

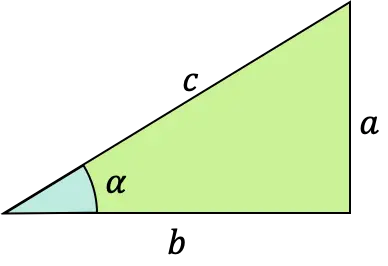
이러한 유형의 수학 함수를 접선, 접선 또는 접선 함수라고도 합니다. 그리고 약어 “tg” 또는 “tan”으로 표현될 수도 있습니다.

탄젠트 함수는 각도의 사인 및 코사인과 함께 가장 잘 알려진 세 가지 삼각비 중 하나입니다.

탄젠트 함수의 특성값

자주 반복되는 특정 각도가 있으므로 이러한 각도에서 접선 함수의 값을 아는 것이 편리합니다.

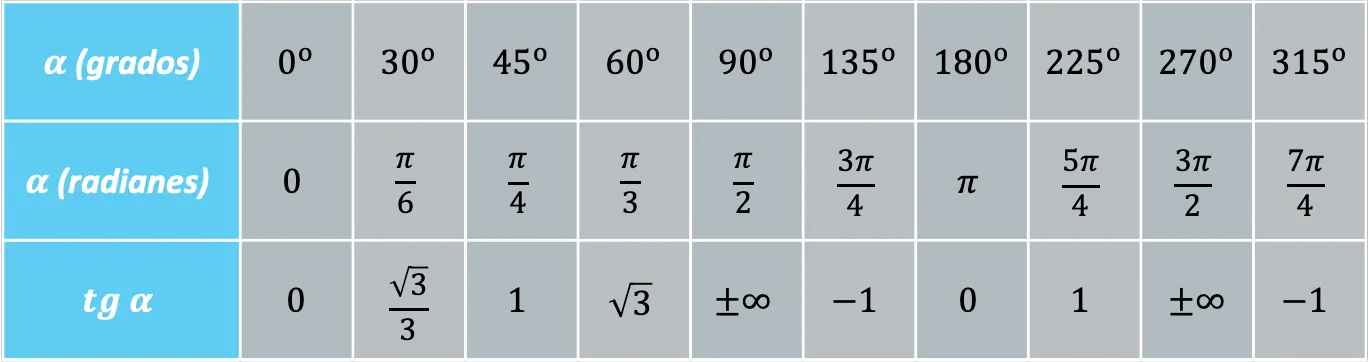
반면, 탄젠트 함수는 다음과 같은 기본 삼각법 항등식을 통해 사인 및 코사인 함수에 연결될 수 있습니다.

$\text{tg } \alpha = \cfrac{\text{sen }\alpha}{\text{cos }\alpha}$

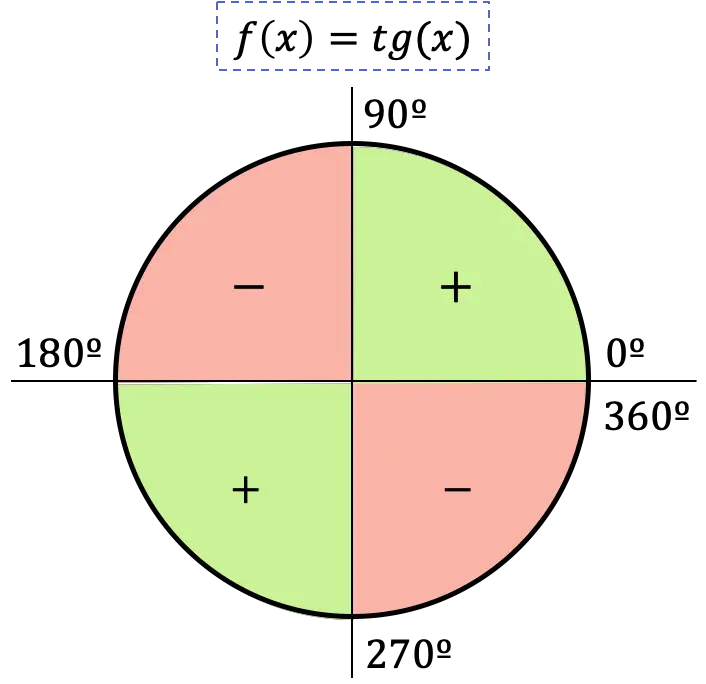
따라서 접선 함수의 부호는 각도가 위치한 사분면에 따라 달라집니다.

각도가 첫 번째 사분면에 속하면 접선은 양수입니다. 이 사분면에서 사인과 코사인도 양수이기 때문입니다.
각도가 두 번째 사분면에 있으면 접선은 음수가 됩니다. 왜냐하면 이 사분면에서 사인은 양수이지만 코사인은 음수이기 때문입니다.
각도가 세 번째 사분면에 있으면 접선은 양수입니다. 왜냐하면 이 사분면에서 사인과 코사인이 음수이기 때문입니다.
각도가 네 번째 사분면에 있으면 접선은 음수가 됩니다. 왜냐하면 이 사분면에서 사인은 음수이고 대신 코사인은 양수이기 때문입니다.

탄젠트 함수의 그래픽 표현

이전 섹션에서 본 값 표를 사용하여 접선 함수를 그래프로 표시할 수 있습니다. 그리고 탄젠트 함수를 그래프로 나타내면 다음과 같은 결과를 얻을 수 있습니다.

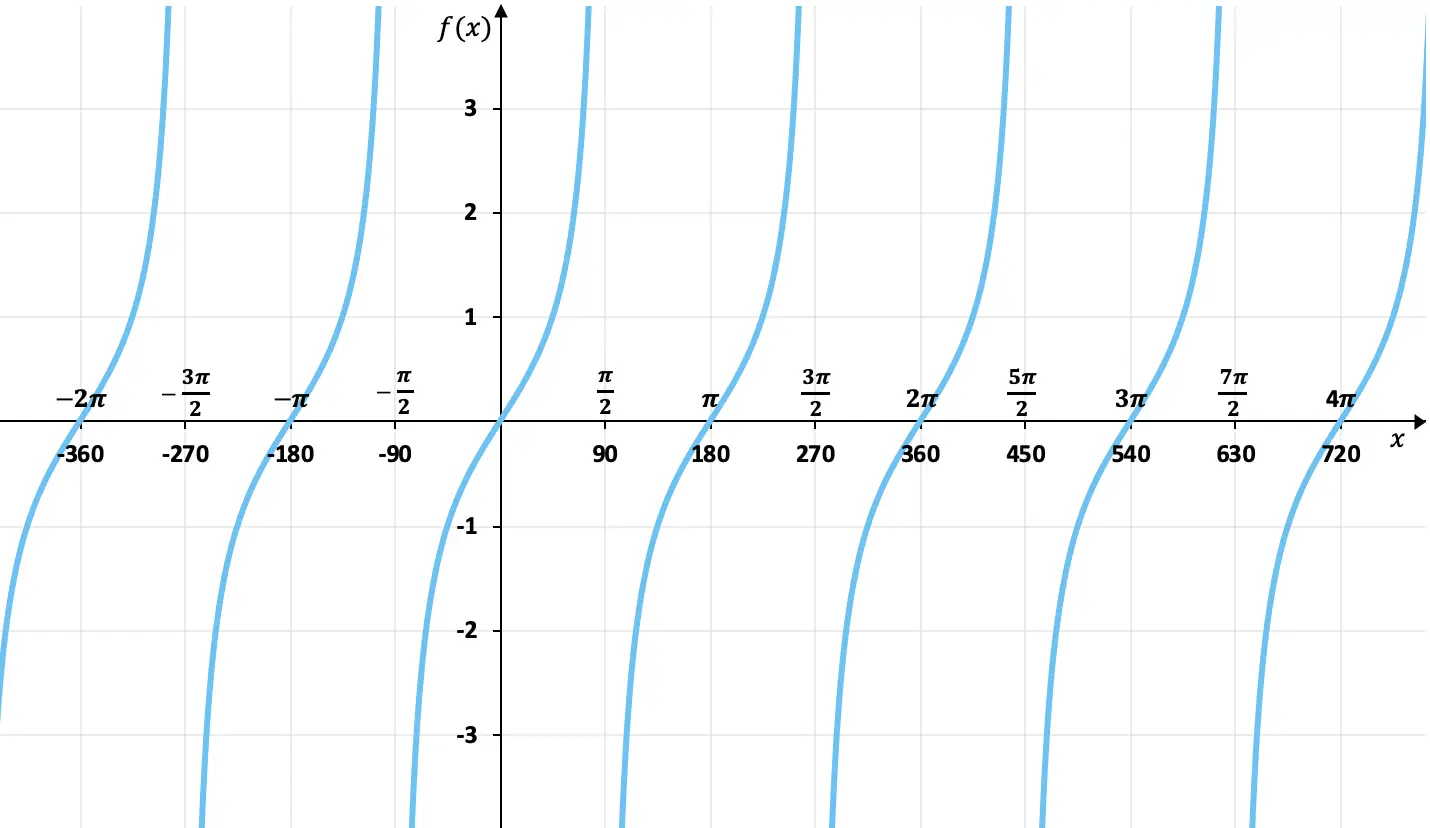
그래프에서 볼 수 있듯이 탄젠트 함수의 이미지 값은 사인, 코사인 함수와 달리 경계가 없습니다. 추가적으로 그 값은 180도(π 라디안)마다 반복되므로 주기가 180°인 주기함수 입니다.

반면, 이 그래프에서는 접선 함수가 홀수 라는 것을 알 수 있습니다. 그 이유는 반대 요소가 반대 이미지를 갖기 때문입니다. 즉, 원점(0,0)을 기준으로 대칭입니다. 예를 들어, 45°의 접선은 1의 가치가 있고 -45°의 접선은 -1의 가치가 있습니다.

마지막으로, 접선 함수에 수직 점근선이 있다는 것도 볼 수 있습니다. 예를 들어 x=90° 선에 매우 가깝지만 절대 닿지 않으며 180도마다 같은 일이 발생합니다. 이는 이 지점에서 함수의 한계가 무한대에 가까워지는 경향이 있음을 의미합니다.

접선 함수의 속성

탄젠트 함수에는 다음과 같은 특징이 있습니다.

접선 함수의 정의역은 수직 점근선이 있는 점을 제외한 모든 실수입니다.

$\displaystyle \text{Dom } f = \mathbb{R} - \left\{(2k+1)\cdot \frac{\pi}{2} \right\} \qquad k \in \mathbb{Z}$

$\displaystyle \text{Dom } f = \mathbb{R} - \left\{\ldots \ , \ -\frac{\pi}{2} \ , \ \frac{\pi}{2} \ , \ \frac{3\pi}{2} \ , \ \ldots \right\}$

탄젠트 함수의 범위 또는 범위는 모두 실수입니다.

$\text{Im } f= \mathbb{R}$

주기성이 π인 연속적이고 홀수 함수입니다.

$\displaystyle \text{tg}(-x) =- \text{tg }x$

이러한 유형의 삼각 함수는 점 (0,0)에서 y축(Y축)과의 단일 교차점을 갖습니다.

$(0,0)$

대신 pi의 여러 좌표에서 가로좌표(X축)를 주기적으로 가로챕니다.

$\displaystyle (k\pi ,0) \qquad k \in \mathbb{Z}$

이 함수는 전체 영역에 걸쳐 엄격하게 증가하므로 최대값도 최소값도 없습니다.

탄젠트의 미분은 다음과 같습니다.

$f(x)=\text{tg } x \ \longrightarrow \ f'(x)= 1+\text{tg}^2 x=\cfrac{1}{\text{cos}^2 x} =\text{sec}^2 x$

마지막으로 탄젠트 함수의 적분은 다음과 같습니다.

$\displaystyle \int \text{tg } x \ dx= -\ln \lvert \text{cos }x \rvert + C$

접선 함수의 주기

사인, 코사인 등 다른 삼각 함수와 달리 탄젠트 함수는 최대값과 최소값이 없으므로 크기가 없습니다. 그러나 이는 주기적인 함수입니다. 즉, 그래프에서 본 것처럼 해당 값이 빈도로 반복됩니다.

$\displaystyle f(x)= \text{tg}(wx)$

탄젠트 함수의 주기는 그래프가 반복되는 두 점 사이의 거리로, 다음 공식으로 계산됩니다.

$\displaystyle \text{Periodo}=T=\cfrac{\pi}{w}$

탄젠트 정리

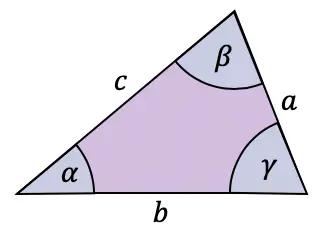
접선 공식은 일반적으로 직각 삼각형에 사용되지만 모든 유형의 삼각형에 적용할 수 있는 정리인 접선 정리도 있습니다.

접선 정리는 삼각형의 변과 각도를 다음과 같이 연결합니다.

$\displaystyle \cfrac{a+b}{a-b} = \cfrac{ \text{tg}\left(\frac{\alpha+\beta}{2}\right)}{\text{tg}\left(\frac{\alpha-\beta}{2}\right)}$

$\displaystyle \cfrac{a+c}{a-c} = \cfrac{ \text{tg}\left(\frac{\alpha+\gamma \vphantom{\beta}}{2}\right)}{\text{tg}\left(\frac{\alpha-\gamma\vphantom{\beta}}{2}\right)}$

$\displaystyle \cfrac{b+c}{b-c} = \cfrac{ \text{tg}\left(\frac{\beta+\gamma}{2}\right)}{\text{tg}\left(\frac{\beta-\gamma}{2}\right)}$

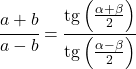
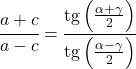
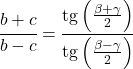
접선 함수와 다른 삼각비의 관계

아래에는 삼각법의 가장 중요한 삼각비와 접선의 관계가 나와 있습니다.

유방과의 관계

각도의 탄젠트와 사인은 다음과 같은 관계가 있습니다.

$\displaystyle \text{tg }\alpha = \pm \cfrac{\text{sen }\alpha }{\sqrt{1-\text{sen}^2\alpha \vphantom{\bigl( }}}$

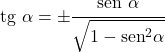
코사인 비율

마찬가지로 각도의 탄젠트와 코사인은 다음 동등성과 관련됩니다.

$\displaystyle \text{tg }\alpha = \pm \cfrac{\sqrt{1-\text{cos}^2\alpha \vphantom{\bigl( }} }{\text{cos }\alpha}$

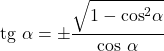
코시컨트와의 관계

증명하기는 어렵지만 탄젠트는 코시컨트에만 의존하도록 풀 수 있습니다.

$\displaystyle \text{tg }\alpha = \pm \cfrac{1}{\sqrt{\text{csc}^2\alpha -1 \vphantom{\bigl( }}}$

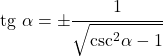
시컨트와의 관계

각도의 접선과 시컨트는 다음 방정식과 관련됩니다.

$\displaystyle \text{tg }\alpha = \pm\sqrt{\text{sec}^2\alpha -1$

코탄젠트와의 관계

탄젠트와 코탄젠트는 곱셈의 역수입니다.

$\displaystyle \text{tg }\alpha =\pm \cfrac{1}{\text{cot }\alpha}$