거듭제곱(또는 잠재적 함수)의 파생

9월 17, 2023

여기에서는 거듭제곱(또는 잠재 함수)을 유도하는 방법을 설명하고, 거듭제곱의 파생 공식과 몇 가지 예를 찾을 수 있으며, 단계별로 연습문제를 풀어 연습할 수도 있습니다.

거듭제곱의 미분 공식

거듭제곱 또는 전위 함수의 도함수는 거듭제곱의 지수에 밑의 도함수를 뺀 지수에서 밑의 도함수의 1을 곱한 값입니다.

$f(x)=u^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot u^{k-1}\cdot u'$

따라서 밑이 항등 함수 인 경우 거듭제곱을 얻으려면 함수에 지수를 곱하고 지수에서 한 단위를 빼면 됩니다.

$f(x)=x^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot x^{k-1}$

실제로 항등함수의 미분은 1과 같습니다.

요약하자면, 잠재 함수를 도출하려면 두 가지 공식이 있습니다. 첫 번째는 항상 사용할 수 있고 두 번째는 밑이 x일 때만 적용할 수 있습니다.

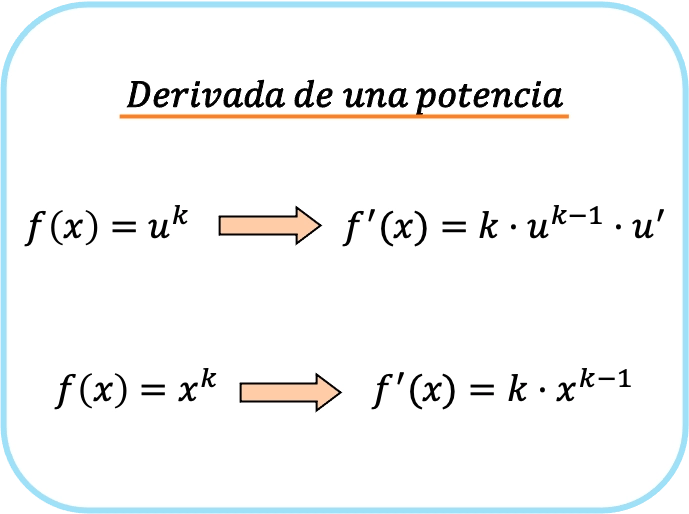
힘에서 파생된

우리는 거듭제곱의 도함수에 대해 제시된 첫 번째 공식이 두 번째 공식과 같지만 체인 규칙을 적용한다는 것을 쉽게 확인할 수 있습니다.

이 공식은 변수가 거듭제곱인 경우에만 사용할 수 있으며, x가 분모에 있는 경우 지수 함수의 도함수에 대한 규칙을 적용해야 합니다.

➤ 참조: 지수 함수의 미분

거듭제곱 미분의 예

잠재 함수의 도함수에 대한 공식을 본 후에는 거듭제곱이 어떻게 도출되는지 이해할 수 있도록 이러한 유형의 도함수에 대한 몇 가지 예를 설명할 것입니다.

예 1: 기본 거듭제곱 x의 미분

$f(x)=x^4$

이전 섹션에서 설명했듯이 거듭제곱의 밑이 x일 때 함수를 도출하기 위해 사용해야 하는 공식은 다음과 같습니다.

$f(x)=x^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot x^{k-1}$

따라서 4의 거듭제곱 x의 도함수는 다음과 같습니다.

$f(x)=x^4 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=4\cdot x^{4-1}=4x^3$

예 2: 괄호를 사용한 거듭제곱의 파생

$f(x)=(2x-1)^5$

이 예에서 밑은 항등 함수가 아니므로 거듭제곱의 도함수에 대한 일반 공식을 사용해야 합니다.

$f(x)=u^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot u^{k-1}\cdot u'$

괄호 안의 함수는 선형 함수이므로 그 도함수는 2입니다. 따라서 전체 전위 함수의 도함수는 다음과 같습니다.

$f(x)=(2x-1)^5 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=5\cdot (2x-1)^4\cdot 2=10(2x-1)^4$

예시 3: 음의 거듭제곱의 미분

$f(x)=(\log 9x)^{-2}$

이 경우 지수가 음수이고 밑이 로그인 잠재적 함수가 있으므로 다음 공식을 사용하여 함수를 차별화합니다.

$f(x)=u^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot u^{k-1}\cdot u'$

거듭제곱 지수가 음수이더라도 그 지수에서 1을 빼야 합니다. 따라서 함수의 미분은 다음과 같습니다.

$f'(x)=-2\cdot (\log 9x)^{-3}\cdot \cfrac{1}{9x\cdot \ln 10}\cdot 9 =\cfrac{-2(\log 9x)^{-3}}{x\ln 10}$

해법에 대해 의문이 있는 경우 여기에서 로그 함수의 미분 공식을 참조할 수 있습니다.

➤ 참고: 로그 함수의 미분

예 4: 근이 있는 거듭제곱의 파생

$f(x)=\sqrt[3]{(5x+2)^7}$

이 예의 함수는 정규식 내의 거듭제곱입니다. 그러나 근호는 전위 표현식으로 변환될 수 있으므로 분수 지수가 있는 전위 함수로 변환하여 함수를 단순화할 수 있습니다.

$f(x)=(5x+2)^{\frac{7}{3}}$

이제 변수 거듭제곱의 미분 공식을 적용합니다.

$f(x)=u^k \quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=k\cdot u^{k-1}\cdot u'$

그리고 파생물은 다음과 같습니다.

$f'(x)=\cfrac{7}{3}\cdot (5x+2)^{\frac{7}{3}-1} \cdot 5=\cfrac{35}{3}(5x+2)^{\frac{4}{3}}$

근미분 규칙을 사용하여 이러한 유형의 함수를 구별할 수도 있습니다.

➤ 참조: 루트에서 파생됨

거듭제곱의 미분에 대한 해결 연습

다음 거듭제곱의 미분을 계산합니다.

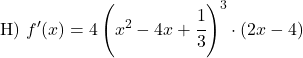
$\text{A) } f(x)=x^8$

$\text{B) } f(x)=3x^5$

$\text{C) } f(x)=-2x^{-4}$

$\text{D) } f(x)=(3x^2-4x)^6$

$\text{E) } f(x)=6(x^2+10)^3$

$\text{F) } f(x)=\cfrac{1}{(9x+2)^3}$

$\text{G) } f(x)=\sqrt{4x^5}$

$\text{H) } \displaystyle f(x)=\left(x^2-4x+\frac{1}{3}\right)^4$

$\text{I) } f(x)=\text{sen}^3(6-2x)$

솔루션 보기

$\text{A) } f'(x)=8x^7$

$\text{B) } f'(x)=15x^4$

$\text{C) } f'(x)=8x^{-5}$

$\text{D) } f'(x)=6(3x^2-4x)^5\cdot (3x-4)$

$\text{E) } f'(x)=3\cdot 6(x^2+10)^2 \cdot 2x=36x(x^2+10)^2$

$\text{F) } f'(x)=-3\cdot (9x+2)^{-4}\cdot 9 =-27(9x+2)^{-4}$

$\text{G) } f'(x)=\cfrac{5}{2}\cdot 2x^{\frac{5}{2}-1} =5x^{\frac{3}{2}}$

$\text{H) } \displaystyle f'(x)=4\left(x^2-4x+\cfrac{1}{3}\right)^3\cdot (2x-4)$

$\text{I) } f'(x)=3\text{sen}^2(6-2x)\cdot \text{cos}(6-2x)\cdot (-2)=-6x\cdot \text{sen}^2(6-2x)\cdot \text{cos}(6-2x)$

댓글 달기 댓글 취소