이 글에서는 함수의 주기성이 무엇인지 설명합니다. 또한 주기 함수의 몇 가지 예를 볼 수 있습니다. 마지막으로 삼각함수의 주기는 가장 중요한 특징 중 하나이기 때문에 분석하겠습니다.
함수의 주기성은 무엇입니까?
함수의 주기성은 그 값을 주기적으로 반복하는 함수의 특징입니다. 즉, 그래프가 특정 간격마다 반복되면 함수는 주기적입니다. 이 간격을 기간이라고 합니다.
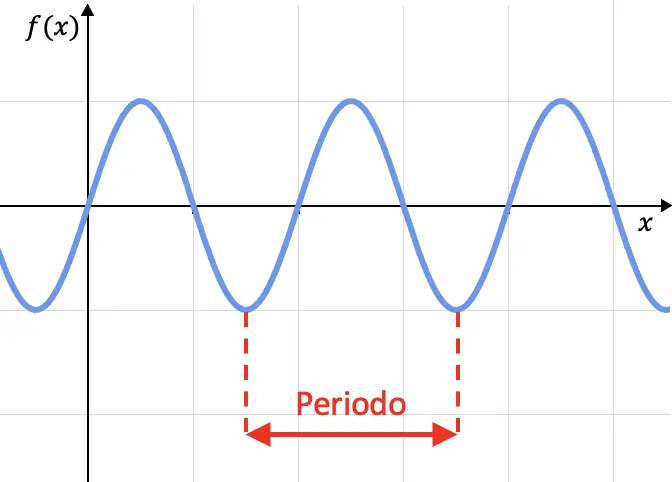
수학적으로 함수는 함수가 충족되는 경우만 주기적으로 정의됩니다.
![]()
독립 변수 x의 모든 값에 대해.
![]()
여기서 T는 주기 함수 i k 정수의 주기입니다.
함수 주기성의 예
함수의 주기성 개념을 살펴본 후에는 함수의 주기성을 계산하는 방법에 대한 몇 가지 예를 살펴보겠습니다.
실시예 1
다음 함수가 주기적인지 확인합니다.
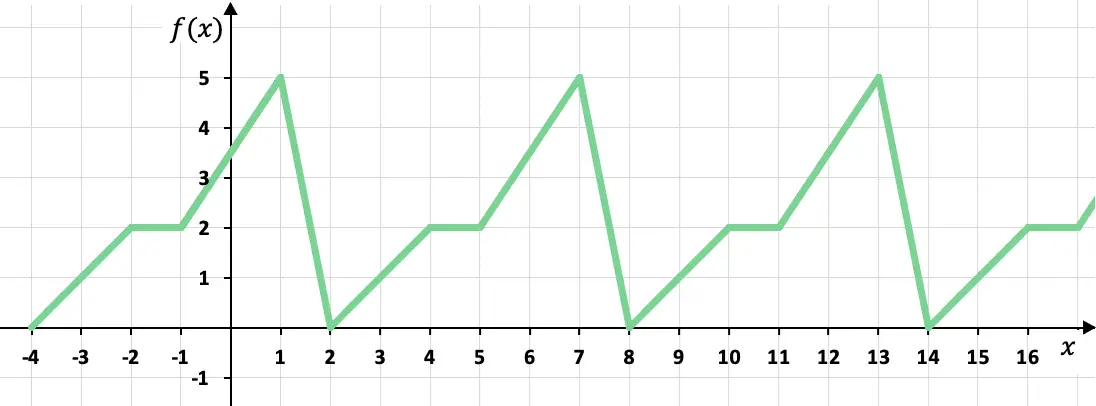
이 조각별로 정의된 함수는 그래프의 값이 주기적으로 반복되므로 주기 함수입니다. 보다 정확하게는 함수는 6 x마다 동일한 값을 취하므로 함수의 주기는 6과 같습니다.
![]()
실시예 2
다음 함수의 주기성을 구합니다.
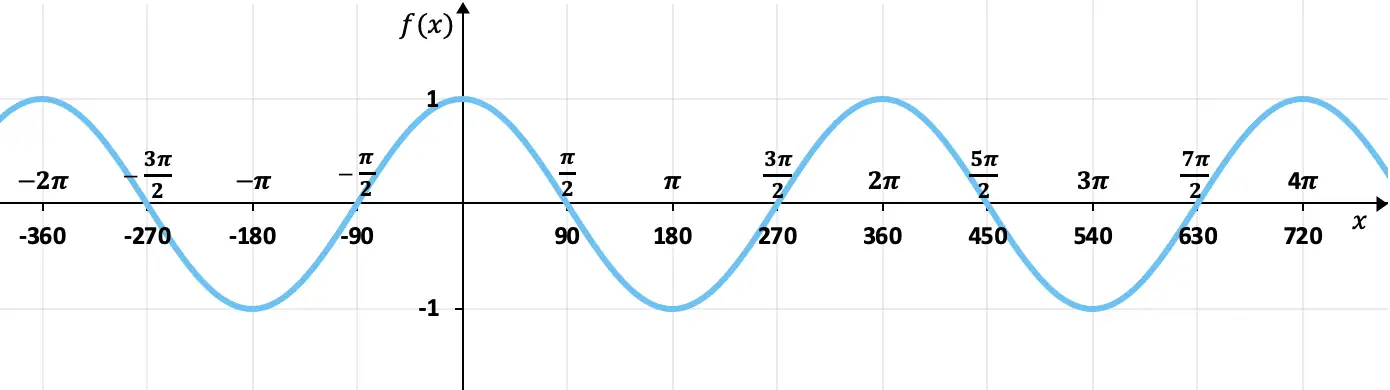
이 함수는 삼각 함수, 더 정확하게는 코사인 함수의 그래픽 표현에 해당합니다.
그래프에서 볼 수 있듯이, 함수는 자신의 값을 주기적으로 반복하므로 주기함수이다. 또한 파동의 정점과 정점 사이에는 2π(또는 360°)의 공간이 있으므로 이것이 함수의 주기입니다.
![]()
삼각함수의 주기성
주기성과 삼각 함수는 밀접하게 관련되어 있습니다. 실제로 이러한 유형의 함수의 주요 특징 중 하나는 대부분의 삼각 함수가 주기적이라는 것입니다.
다음으로 사인, 코사인, 탄젠트 등 3가지 주요 삼각 함수의 주기성을 연구합니다.
사인 함수 기간
사인 함수의 표현식은 다음과 같습니다.
![]()
이 경우, 주기를 찾기 위해 함수를 그래프로 표시할 필요는 없지만, 다음 공식을 적용하면 간단히 계산할 수 있습니다.
![]()
또한 사인 함수에는 주기를 변경하면 그래프의 모양도 변경된다는 특징이 있습니다. 다음 링크에서 기간 값이 그래픽 표현에 어떤 영향을 미치는지 확인할 수 있습니다.
➤ 참조: 사인 함수 그래프
코사인 함수의 주기
코사인 함수의 대수적 표현은 다음과 같습니다.
![]()
사인과 마찬가지로 코사인 함수의 주기는 다음 공식을 사용하여 직접 찾을 수 있습니다.
![]()
코사인 기간의 값에 따라 그래프가 완전히 결정됩니다. 다음 링크를 클릭하여 그 이유를 알아보세요.
➤ 참조: 코사인 함수 그래프
접선 함수의 주기
탄젠트 함수는 수학적으로 설명됩니다.
![]()
탄젠트 함수의 주기는 사인 및 코사인의 주기와 동일한 공식으로 계산됩니다.
![]()
그러나 탄젠트 함수 그래프는 주기적으로 반복되는 점근선도 가지고 있다는 점에서 사인, 코사인과 다릅니다. 다음 링크에서 이 삼각 함수의 기능과 기타 기능을 볼 수 있습니다.
➤ 참조: 접선 함수 그래프