고대부터 자연수의 집합은 수학의 많은 분야가 구축되는 기초가 되어 왔습니다. 예를 들어 산술과 기하학은 이러한 숫자를 기반으로 합니다. 그렇기 때문에 이 짧은 기사에서 우리는 자연수의 정의와 이 집합과 관련된 모든 개념을 볼 것입니다.
자연수란 무엇입니까?
자연수는 물리적 세계에서 물체의 수를 세고 순서를 지정 하는 데 사용하는 추상 요소 집합입니다. 수학에서 자연수의 집합은 일반적으로 문자 ℕ로 표시됩니다. 이는 소수가 없고 분수가 아닌 모든 양의 정수로 구성됩니다: ℕ = {1, 2, 3, 4, 5, 6…}.
즉, 자연수는 실제 물체의 개수를 세는 데 사용할 수 있는 모든 양의 정수 입니다. 이런 식으로 우리는 숫자 1을 실제 물체의 수를 세는 데 사용할 수 있기 때문에 자연수라고 말할 수 있습니다. 예를 들어, 사과 1개와 배 2개가 있으면 총 3개의 과일이 됩니다.
다음 이미지에서는 모든 숫자 집합을 요약한 다이어그램을 보여 주므로 집합 ℕ이 어디에 있는지 확인할 수 있습니다. 그리고 자연수의 개념을 더 잘 동화시키기 위해 다른 것들과 어떤 관계가 있습니까? 설명을 계속하기 전에 개념도를 잘 살펴보고 이해하는 것이 좋습니다.

숫자가 자연수인지 아닌지 어떻게 알 수 있나요?
우리가 이미 말했듯이, 자연수는 우리가 계산하고 주문하는 데 사용하는 숫자입니다. 값이 자연값인지 아닌지를 알려면 다음 사항을 염두에 두어야 합니다. 숫자 ℕ에는 음수 기호가 없고 소수 자릿수가 없으며 허수 단위가 없고 분수가 아닙니다. 다음으로, 처음 100개의 자연수 목록을 보여드리겠습니다.
1장, 2장, 3장, 4장, 5장, 6장, 7장, 8장, 9장, 10장, 11장, 12장, 13장, 14장, 15장, 16장, 17장, 18장, 19장, 20장, 21장, 22장, 23장, 24장, 25장, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 6 4, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75 , 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99 및 100 .
자연수는 어떻게 읽고 쓰나요?
자연수는 십진수 체계를 따릅니다. 즉, 값의 산술 밑수는 10입니다. 모든 숫자는 1, 2, 3, 4, 5, 6, 7, 8, 9 등 9개의 숫자 중 적어도 하나로 구성됩니다. 그리고 어떤 경우에도 자연수에는 소수점이나 음수 부호가 없다는 점을 기억하십시오. .
모든 산술 연산에 관한 한 이 숫자는 수학 표기법 에 따라 작성됩니다. 기호 나 표현식 에 대해 의문이 있는 경우 이 마지막 링크에 액세스하여 기사를 읽어 보시기 바랍니다. 여기서는 수학 언어 및 모든 표기법과 관련된 모든 정보를 찾을 수 있습니다.
자연수의 특성
자연수의 가장 중요한 특성 중 일부는 다음과 같습니다.
- 첫 번째 자연수는 1입니다. 0은 자연수가 아니기 때문입니다.
- 측정, 제어 및 계산에 사용됩니다. 길이, 무게, 용량 등을 측정하는 데 사용할 수 있습니다.
- 그들은 서로 비교할 수 있습니다. 어느 것이 다른 자연수보다 크거나 작은지 말할 수 있습니다.
- 순서가 있습니다. 자연수는 1에서 시작하여 무한대에서 끝나는 논리적 순서를 따릅니다.
- 두 명의 자연인은 동일한 후계자나 동일한 전임자를 가질 수 없습니다.
- 자연수는 소수나 분수가 아닌 양의 정수이기 때문에 모든 자연수는 정수입니다.
이 섹션을 마무리하기 위해 학생들 사이에서 종종 의심을 불러일으키는 이 세트에 대한 일련의 설명을 제공합니다. 숫자 0은 자연수가 아니며 자연수는 정수이며 자연수는 음수가 될 수 없으며 자연수에는 소수가 없습니다. 장소와 자연수는 무한합니다.
자연수의 표현
ℕ라고도 불리는 자연수의 집합은 1, 2, 3, 4… 등의 양의 정수로 구성됩니다. 이 집합은 다음 표기법으로 표시됩니다: ℕ = {1, 2, 3, 4, 5…}. 그러나 수직선 에 배치하여 보다 그래픽적으로 표시할 수도 있습니다.
두 번째 방법은 수평선을 직선으로 그리고 그 선을 따라 자연수의 값을 순서대로 쓰는 것입니다. 따라서 집합의 순서를 쉽게 시각화할 수 있으며, 이 시스템은 이 숫자 집합을 배우는 사람들에게 매우 좋습니다. 다음 이미지에서 행 레이아웃이 어떻게 보이는지 확인할 수 있습니다.
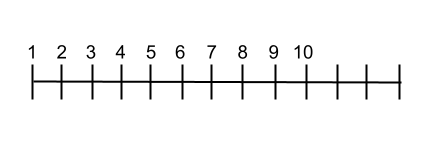
자연수를 이용한 연산
이제 집합 ℕ의 모든 특성과 속성을 알았으므로 이를 산술 연산 에 적용할 차례입니다. 이는 이러한 숫자의 주요 응용 프로그램입니다. 다음으로 4가지 기본 연산(덧셈, 뺄셈, 곱셈, 나눗셈)에 대해 자세히 설명하겠습니다.
자연값을 더하면 또 다른 숫자 ℕ( 3 + 6 = 9) 을 얻게 됩니다. 그러나 자연수 사이에서 뺄셈을 하면 그 결과는 양수가 될 수도 있고 음수가 될 수도 있습니다. 후자는 우리가 말하는 집합에 속하지 않으므로 양의 결과를 갖는 뺄셈만이 집합 ℕ: 4 – 2 = 2 의 일부입니다.
자연수 사이의 곱셈은 덧셈과 동일합니다. 왜냐하면 양수만 나올 수 있기 때문입니다. 예를 들어, 3과 8을 곱하면 3 · 8 = 24가 됩니다. 그러나 집합 ℕ의 숫자를 나누면 어떤 경우에는 십진수 를 얻을 수 있습니다. 이 상황에서 결과는 자연적인 전체의 일부가 아닙니다.
따라서 자연수의 집합에서는 덧셈과 곱셈만이 정의된다. 이 두 가지 작업은 교환 및 결합 속성을 확인합니다. 따라서 초기 숫자가 자연수이면 항상 자연수가 됩니다. 이러한 방식으로 이는 항상 집합 ℕ의 속성을 존중하는 작업입니다.
자연수의 응용
자연수는 일상생활 에서 자주 사용됩니다. 예를 들어 테이블의 길이나 사람이 상점까지 걸어가는 데 걸리는 시간을 측정하는 데 사용할 수 있습니다. 또한 덧셈이나 뺄셈과 같은 수학적 계산을 수행하는 데에도 사용할 수 있습니다. 정수는 선반에 책을 놓는 것과 같이 공간에서 객체의 위치를 결정하는 데에도 사용될 수 있습니다.