이 페이지에서는 일반 행렬이 무엇인지와 일반 행렬의 예를 볼 수 있습니다. 또한 이러한 유형의 행렬의 특성과 연습문제를 단계별로 찾아볼 수 있습니다.
정규 행렬이란 무엇입니까?
일반적인 배열 정의는 다음과 같습니다.
정규 행렬은 켤레 전치 행렬을 곱한 복소 행렬이며 그 자체로 켤레 전치의 곱과 같습니다.
금
는 다음의 켤레 전치 행렬입니다.
.
그러나 실수 행렬인 경우 이전 조건은 행렬이 전치로 교환된다는 의미입니다. 즉, 다음과 같습니다.
분명히 실수 행렬의 켤레 전치 행렬은 단순히 전치(또는 전치) 행렬이기 때문입니다.
정규 행렬의 예
복소수의 예
다음과 같은 2×2 차원의 복소 정사각 행렬은 정상입니다.
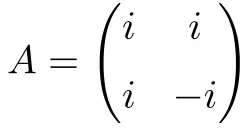
그 정상성에 대한 시연은 아래에 첨부되어 있습니다:
![\displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f44b98cec879a8332c462d2393fbfbba_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fddc406493ac1c81c86edf1ad6e58d0b_l3.png "Rendered by QuickLaTeX.com")
실수의 예
2차 실수를 갖는 다음 정사각 행렬도 정규입니다.
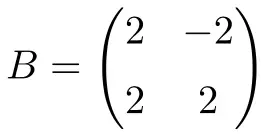
이 경우에는 실수만 있기 때문에 정규임을 증명하려면 행렬이 전치로 교환 가능하다는 것을 검증하면 충분합니다.
![\displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a320a8e300315c6a48bb8095266408ca_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6ad5bd62deeb5bcbf561a2ee6b29741_l3.png "Rendered by QuickLaTeX.com")
일반 행렬의 속성
일반 행렬은 다음과 같은 특징을 가지고 있습니다.
- 모든 일반 행렬은 대각화 가능 행렬입니다.
- 각 유니터리 행렬은 또한 일반 행렬입니다.
- 마찬가지로 에르미트 행렬(Hermitian Matrix)은 정규 행렬입니다.
- 마찬가지로, 반에르미트 행렬은 정규 행렬입니다.
- A가 정규 행렬인 경우 켤레 전치 행렬 A*의 고유값(또는 고유값)은 A의 켤레 고유값입니다.
![\displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i](https://mathority.org/wp-content/ql-cache/quicklatex.com-a91ee46b5f8dda0d51ecb57474f5b816_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i](https://mathority.org/wp-content/ql-cache/quicklatex.com-48c80a017a9afd8b4cf3923757f4e945_l3.png "Rendered by QuickLaTeX.com")
- 정규 행렬에서 서로 다른 고유값과 연관된 고유벡터(또는 고유벡터)는 직교합니다.
- 행렬이 실수로만 구성되어 있고 대칭 인 경우 이는 동시에 일반 행렬입니다.
- 마찬가지로 반대칭 실수 행렬 도 정규 행렬입니다.
- 마지막으로, 실수로 구성된 모든 직교 행렬도 정규 행렬입니다.
일반 행렬에 대한 해결된 연습 문제
연습 1
다음과 같은 2 × 2 차원의 복소 행렬이 정규인지 확인합니다.
![\displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff27d19373c5a4dc8e95472ec295c657_l3.png "Rendered by QuickLaTeX.com")
행렬이 정규임을 보여주기 위해 먼저 켤레 전치(conjugate transpose)를 계산해야 합니다:
![\displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-17c96c654ce5b978f90a905b973d5ae7_l3.png "Rendered by QuickLaTeX.com")
이제 가능한 두 방향 모두에서 행렬 A에 행렬 A*를 곱하여 검증을 수행합니다.
![\displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36212e1d12cf35ea5dd27bd91d77ee56_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3db0fc8fdc948037452b4c6275896686_l3.png "Rendered by QuickLaTeX.com")
두 곱셈의 결과는 동일하므로 행렬 A는 정규 행렬입니다.
연습 2
다음과 같이 크기가 2 × 2인 실수 행렬이 정규 행렬임을 보여주세요.
![\displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854e13859be417985691b5ed6d2a050f_l3.png "Rendered by QuickLaTeX.com")
이 경우에는 실수만 있는 환경을 다루기 때문에 행렬 A와 전치 사이의 행렬 곱이 곱셈 방향에 관계없이 동일한 결과를 제공하는지 확인하는 것으로 충분합니다.
![\displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1b6314188f394b3053d3dac0613cf5c_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2b33f892cd29c0ee232b88eaa4946cc_l3.png "Rendered by QuickLaTeX.com")
두 곱의 결과는 동일하므로 행렬 A는 정상입니다.
연습 3
다음 2차 복소수 행렬이 정규 행렬인지 확인합니다.
![\displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00075db37b045e08349f7d5b3f679570_l3.png "Rendered by QuickLaTeX.com")
행렬이 정규인지 확인하려면 먼저 켤레 전치를 계산해야 합니다.
![\displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0b39733376eb2aef269012eb1d6c24be_l3.png "Rendered by QuickLaTeX.com")
이제 행렬 A와 그 공액 전치가 전환 가능한지 확인합니다.
![\displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c207cb9842dacbaf9bc59d4aaff00473_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bcf52f3da81fd7c56b090604c2b6f368_l3.png "Rendered by QuickLaTeX.com")
두 곱셈의 결과는 동일하므로 행렬 A는 정규 행렬입니다.
연습 4
다음과 같은 3×3 차원의 실수 행렬이 정규인지 확인합니다.
![\displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92ee07759c3e6e88af5a68479b5833ea_l3.png "Rendered by QuickLaTeX.com")
행렬은 완전히 실수 요소로 구성되어 있으므로 행렬 A와 전치 사이의 행렬 곱이 곱셈 방향과 무관하다는 것을 검증하는 것으로 충분합니다.
![\displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc7ee02c75239b430c7fc2418f43e343_l3.png "Rendered by QuickLaTeX.com")
![\displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e661b877ee225983c797584e2b61d429_l3.png "Rendered by QuickLaTeX.com")
두 곱의 결과는 동일하므로 행렬 A는 정상입니다.
연습 5
다음과 같은 3×3 차 복소 행렬이 정규 행렬인지 확인합니다.
![\displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-81ca0ac1da07c151a62dcfb06b4be877_l3.png "Rendered by QuickLaTeX.com")
먼저 행렬의 공액 전치를 계산합니다.
![\displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fd0a2dfe1b8bfe18020ab68c1eb3bda6_l3.png "Rendered by QuickLaTeX.com")
이제 우리는 가능한 두 방향 모두에서 행렬 A와 그 켤레 전치 사이의 행렬 곱셈을 수행해야 합니다. 그러나 A의 켤레 전치 행렬은 행렬 A 자체와 동일하므로 에르미트 행렬입니다. 따라서 정규 행렬의 속성을 보면 A는 정규 행렬입니다 . 왜냐하면 모든 에르미트 행렬은 정규 행렬이기 때문입니다.