이 페이지에서는 인자 정리가 무엇인지 설명합니다. 또한, 인수 정리가 다항식의 나눗셈, 근 찾기, 다항식 인수분해 등의 용도로 사용되는 것을 보여줍니다. 마지막으로, 인자 정리에 대한 단계별 연습을 통해 연습할 수 있습니다.
인자 정리는 무엇입니까?
수학에서 인수 정리는 P(a)=0인 경우에만 다항식 P(x)가 (xa) 형식의 다른 다항식으로 나누어진다고 말합니다.
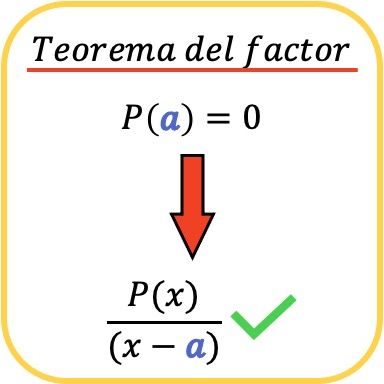
마찬가지로, 인자 정리의 결과로, 다항식 P(x)가 (x−a) 항으로 나누어지면 값 a가 다항식 P( x의 근(또는 0)임을 의미합니다. ) .
하나의 다항식이 다른 다항식으로 나누어진다는 것은 두 다항식 사이의 나눗셈의 나머지(또는 나머지)가 0과 같다는 것을 의미합니다. 이 개념을 완전히 기억하지 못하는 경우 다음 링크에서 다항식 나눗셈의 예를 볼 수 있습니다. 또한 다항식을 나눗셈하는 방법에 대한 설명과 단계별로 해결되는 연습 문제도 찾을 수 있습니다.
인수 정리 예
이제 우리는 인자 정리의 수학적 정의를 알았으니, 그것이 어떻게 적용되는지 알아보기 위해 몇 가지 예를 살펴보겠습니다.
실시예 1
인수 정리의 한 가지 적용은 주어진 다항식이 이항식 으로 나누어지는지 여부를 알아내는 것입니다. 인자 정리를 사용하여 이것이 어떻게 수행되는지에 대한 예를 살펴보겠습니다.
- 다항식 P(x)가 이항식 Q(x)로 나누어지는지 여부를 확인합니다. 두 가지 모두 다음과 같습니다.
![]()
첫째, 제수 다항식 Q(x)는 (xa) 유형의 다항식이므로 인수 정리를 적용하여 문제를 해결할 수 있습니다.
따라서 P(x)를 Q(x)로 나눌 수 있는지 확인하려면 x=1에 대한 다항식 P(x)의 수치 값을 계산해야 합니다. 1은 부호가 변경된 나눗셈 다항식의 독립항이기 때문입니다. :
![Rendered by QuickLaTeX.com \begin{aligned} P(1) & =1^2-4\cdot 1+3 \\[2ex] & = 1-4+3 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-00216efc4a2e53b0b38de1175e73a5bd_l3.png)
x = 1에서 다항식 P(x)의 수치 값은 0을 제공하므로 인수 정리에 따라 P(x)는 Q(x)로 나눌 수 있습니다. 즉, 둘 다로 나눈 나머지는 null이 됩니다.
2개의 다항식을 Ruffini의 정리 로 나누어 나눔성 조건이 충족되는지 확인할 수 있습니다.
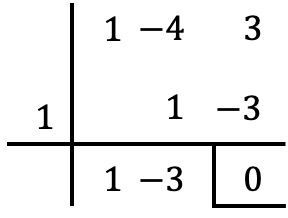
이 예에서 볼 수 있듯이 인자 정리는 나머지(또는 나머지) 정리의 특별한 경우입니다. 나머지 정리가 무엇인지 설명하는 이 글을 남깁니다. 또한 이를 통해 해결된 예제와 연습 문제도 찾을 수 있습니다. 그리고, 게다가 나머지 정리와 인자 정리의 차이가 무엇인지도 알 수 있게 됩니다.
실시예 2
인수 정리는 다항식의 근(또는 0)을 찾는 데에도 사용할 수 있습니다. 그러나 분명히 이러한 유형의 문제를 이해하려면 다항식의 근이 무엇인지 알아야 합니다. 아직도 이 개념을 이해하지 못한다면 링크된 페이지를 참조하세요. 자세히 설명되어 있습니다.
이제 다항식의 근을 찾기 위해 인자 정리가 어떻게 적용되는지 예를 통해 살펴보겠습니다.
- 다항식 P(x)가 주어지면 근 중 하나가 x=2인지 계산합니다.
![]()
인자 정리를 적용하면 x=2라는 항은 x=2에 대한 P(x)의 수치 값이 0인 경우에만 다항식 P(x)의 근이 됩니다. 따라서 우리는 다음과 같은 숫자 값을 찾아야 합니다.
![Rendered by QuickLaTeX.com \begin{aligned} P(2) & =2^3-3\cdot 2^2+5\cdot 2-6 \\[2ex] & = 8-3\cdot 4 +5\cdot 2 -6\\[2ex] & = 8-12+10-6 \\[2ex] & = 0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-82d50f0361613cb6c540051f8da4bc20_l3.png)
실제로 다항식 P(x)의 수치 값은 x=2에서 사라지므로 인수 정리 덕분에 x=2가 다항식 P(x)의 근임을 확인할 수 있습니다.
인수 정리를 사용하여 다항식 인수분해
인자 정리의 또 다른 응용은 다항식의 인수분해 입니다. 그것이 무엇인지 모르는 경우, 다항식을 인수분해한다는 것은 다항식의 표현을 인수의 곱으로 변환하는 것을 의미합니다. 즉, 다항식을 인수분해하면 대수적 표현이 단순화됩니다.
따라서, 계승 정리는 다항식 P(x)가 주어진 값 a에 대해 P(a)=0을 충족하면 해당 다항식의 표현이 곱 P(x)=(xa)· Q(로 인수분해될 수 있음을 확립합니다. x), 여기서 Q(x)는 다항식 P(x)를 (xa)로 나눈 결과인 다항식입니다.
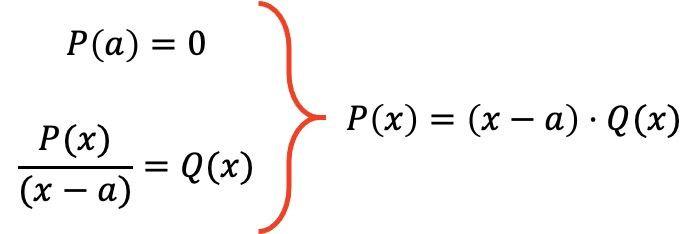
예를 들어, 계승 정리를 사용하여 다음 다항식을 인수분해하겠습니다.
![]()
이전 다항식에서 x=-2에 대한 다항식의 숫자 값이 0이기 때문에 x=-2가 근 중 하나라는 것을 알 수 있습니다.
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =(-2)^3+2\cdot (-2)^2+4\cdot (-2)+8 \\[2ex] & =-8+2\cdot 4+4\cdot (-2)+8 \\[2ex] & = -8+8-8+8 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d94a4657a385e672badeabd7458b376_l3.png)
따라서 우리는 Ruffini의 법칙을 사용하여 x에 의해 형성된 이항식과 근 변경 부호, 즉 인수 (x+2) 사이의 다항식 P(x)를 나눕니다.
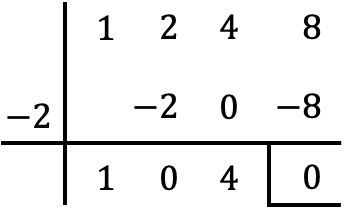
따라서 다항식 나눗셈의 몫은 다음과 같습니다.
![]()
그리고 마지막으로 인수 정리로부터 인수 (x+2)와 이전 나눗셈에서 얻은 몫의 곱셈 형태로 다항식 P(x)를 표현할 수 있습니다.
![]()
따라서 우리는 다항식 P(x)를 인수분해했지만 부분적으로만 수행했습니다. 다항식을 완전히 인수분해하려면 더 긴 절차를 적용해야 합니다. 우리는 Ruffini 다항식을 인수분해하는 방법을 단계별로 가르치는 가이드를 만들었습니다. 또한 이 기사에서는 인수분해의 모든 유형을 설명했으며 해결된 연습문제를 통해 연습할 수 있습니다. 따라서 집합에서 다항식을 인수분해하는 방법을 알아보려면 링크를 클릭하세요.
해결 인자 정리 문제
그런 다음, 인자 정리를 단계별로 풀어서 연습할 수 있도록 여러 가지 연습문제를 준비하여, 이 정리를 이해했는지 확인해보세요. 직접 시도해 보고 솔루션을 올바르게 이해했는지 확인하는 것이 좋습니다. 또한 아래 댓글에 질문을 남길 수 있다는 점도 잊지 마세요! ❓❓💬💬
연습 1
계승 정리를 사용하여 다항식 P(x)가 이항 Q(x)로 나누어 떨어지는지 확인하고, 그렇다면 다항식의 근을 찾아 인수분해합니다.
![]()
이 경우, 다항식 제수 Q(x)는 x와 독립항만으로 구성된 이항식입니다. 따라서 다항식 P(x)가 계승 정리를 사용하여 다른 다항식 Q(x)로 나누어질 수 있음을 보여주기 위해, 제수 다항식 변경 부호의 독립 항에서 다항식 P(x)의 수치 값을 평가해야 합니다. 즉, x=3에서:
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =2\cdot 3^3-4\cdot 3^2+3-7\\[2ex] & = 2\cdot 27-4\cdot 9+3-7 \\[2ex] & = 54-36+3-7\\[2ex] & = 14 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e8ac752f8e16fae1d66386e9d2a02a0_l3.png)
x=3에서 다항식 P(x)의 수치는 14와 동일합니다. 즉, 0과 다릅니다. 따라서 인수 정리에 따르면 나눗셈의 나머지가 0이 아니기 때문에 P(x)는 Q(x)로 나누어지지 않습니다.
연습 2
다항식 P(x)가 이항식 Q(x)로 나누어지는지 여부를 계승 정리로 알아보고, 그렇다면 다항식 P(x)의 근을 찾아 인수분해합니다.
![]()
이 경우 다항식 제수 Q(x)는 x와 독립 항으로만 구성된 이항식이므로 계승 정리를 적용할 수 있습니다.
그리고 다항식 P(x)가 다항식 Q(x)로 나누어질 수 있는지 확인하려면 다항식 Q(x)의 변경된 부호의 독립항에 대한 다항식 P(x)의 수치 값을 찾아야 합니다. 즉, x=-1에서:
![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3+5\cdot (-1)^2+3\cdot (-1)-1\\[2ex] & = -1+5\cdot 1+3\cdot (-1)-1\\[2ex] & = -1+5-3-1\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-34b63772a1b44bee2c746d94b6ca4785_l3.png)
이 문제에서 x=-1에서 다항식의 수치는 0이므로 P(x)는 Q(x)로 나눌 수 있습니다.
그러면 x=-1에서 P(x)의 수치가 사라지기 때문에 x=-1이 다항식 P(x)의 근이라는 계승 정리를 통해 추론할 수 있습니다.
따라서 x=-1은 다항식 P(x)의 근이므로 인수분해하려면 간단히 x+1로 나누면 됩니다. 이를 위해 Ruffini 방법을 사용하겠습니다.
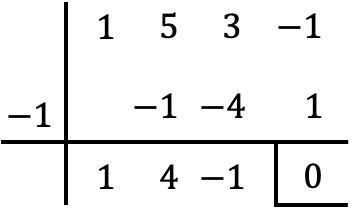
따라서 작업 결과는 다음과 같습니다.
![]()
따라서 다항식 P(x)를 다음과 같이 인수분해할 수 있습니다.
![]()
연습 3
다항식 P(x)가 이항식 Q(x)로 나누어지는지 여부를 계승 정리로 찾아보고, 그렇다면 다항식 P(x)의 근을 찾아 인수분해합니다.
![]()
이 경우, Q(x)를 나누는 다항식은 x와 독립항만으로 구성된 이항식이므로 인자 정리를 이용할 수 있습니다.
그리고 다항식 P(x)가 다항식 Q(x)로 나누어지는지 확인하려면 다항식 Q(x) 변경된 부호의 독립 항에 대한 다항식 P(x)의 수치 값을 결정해야 합니다. 즉, 즉, x =-3에서:
![Rendered by QuickLaTeX.com \begin{aligned} P(-3) & =(-3)^3+5\cdot (-3)^2+4\cdot (-3)-6\\[2ex] & = -27+5\cdot 9+4\cdot (-3)-6\\[2ex] & = -27+45-12-6\\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef8bb895fe041193d71351ffadb94f2f_l3.png)
이 경우 x=-3에서 다항식의 수치는 0이므로 실제로 P(x)는 Q(x)로 나눌 수 있습니다.
이러한 이유로 우리는 계승 정리로부터 x=-3이 다항식 P(x)의 근이라는 것을 추론합니다. 왜냐하면 P(-3)는 0이기 때문입니다.
따라서 x=-3은 다항식 P(x)의 근이므로 이를 인수분해하려면 x+3으로 나누어야 합니다. 그리고 이를 위해 Ruffini의 규칙을 사용합니다.
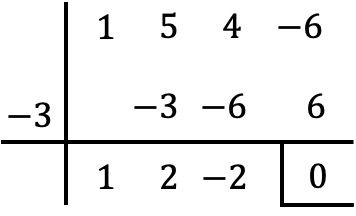
따라서 나눗셈의 결과는 다음과 같습니다.
![]()
따라서 다항식 P(x)를 다음과 같은 방식으로 인수분해할 수 있습니다.
![]()
인자 정리에 대해 어떻게 생각하시나요? 그것이 대수학에서 유용하다고 생각하시나요? 댓글에서 여러분의 의견을 읽었습니다!
🙌⬇⬇⬇🙌