뉴턴의 이항식(이항정리)

이 페이지에서는 뉴턴의 이항식(또는 이항정리)이 무엇인지, 그리고 그 공식이 무엇인지에 대한 설명을 찾을 수 있습니다. Tartaglia(또는 Pascal) 삼각형을 사용하여 이것이 어떻게 단순화될 수 있는지 확인할 수도 있습니다. 또한 뉴턴의 이항식과 그 모든 속성에 대한 단계별 해결 연습을 찾을 수 있습니다. 마지막으로, 우리는 이 특별한 정리의 기원 뒤에 숨겨진 호기심을 설명할 것입니다.

뉴턴의 이항식은 무엇입니까?

수학에서 이항 정리라고도 알려진 뉴턴의 이항식은 이항식의 거듭제곱을 쉽게 계산할 수 있는 공식입니다. 즉, 뉴턴의 이항식은 (a+b) 형태의 대수적 표현을 풀 수 있는 공식으로 구성됩니다.

분명히 이 정리는 물리학자, 수학자, 철학자 아이작 뉴턴 경의 이름을 따서 명명되었습니다. 그러나 이 정리가 이미 사용된 중동 문헌이 발견되었기 때문에 이와 관련하여 약간의 논란이 있습니다. 아래에서 우리는 이 수학 공식의 기원에 대해 심도있게 논의할 것입니다.

뉴턴의 이항식

뉴턴의 이항식 정의에서 보았듯이 이 정리는 이항식의 거듭제곱을 풀기 위해 사용됩니다. 그런데… 뉴턴의 이항식은 어떻게 적용되나요? 아니면, 즉, 뉴턴의 이항식은 무엇입니까?

뉴턴의 이항식의 수학 공식은 다음과 같습니다.

\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}a^{n-k}b^k

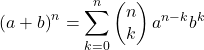
또는 이에 상응하는 것:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

뉴턴의 이항식의 개념을 이해하기에는 공식이 다소 복잡하므로, 여러분이 더 잘 이해할 수 있도록 아래에 가장 낮은 차수의 이항식의 힘을 제시했습니다.

뉴턴의 이항 정리 공식

보시다시피, 이항식을 전개하면 조합수의 하위 요소가 증가 하는 것처럼 첫 번째 항(a)의 지수는 감소하고 두 번째 항(b) 의 지수는 증가합니다.

따라서 이항정리를 이용하기 위해서는 조합수, 즉 유형의 대수적 표현을 푸는 방법을 알아야 한다.

\begin{pmatrix} 4 \\ 2 \end{pmatrix}

. 따라서 뉴턴 이항식을 계산하는 방법의 예를 살펴보기 전에 조합수에 대해 간략하게 살펴보겠습니다.

조합 번호

조합수 (또는 이항 계수)를 결정하려면 다음 공식을 적용해야 합니다.

\begin{pmatrix}n \\ k \end{pmatrix} = \cfrac{n!}{k!(n-k)!}

금

n!

그리고

k!

이것은 팩토리얼 숫자 입니다. 팩토리얼 숫자는 모든 양의 정수 1에 해당 숫자를 곱하여 계산된다는 점도 기억하세요.

n! = 1 \cdot 2 \cdot 3 \cdots (n-1) \cdot n

예를 들어, 조합 번호를 찾아 그것이 어떻게 수행되는지 확인할 수 있습니다.

\begin{pmatrix} 4\\ 3 \end{pmatrix} = \cfrac{4!}{3!(4-3)!}=\cfrac{4!}{3!\cdot 1!}= \cfrac{1 \cdot 2\cdot 3 \cdot 4}{(1 \cdot 2\cdot 3) \cdot 1} = \cfrac{24}{6} = 4

조합 숫자는 키를 사용하여 계산기를 통해 결정할 수도 있습니다.

\boxed{nCr}.

뉴턴 이항식 예

이제 이항 정리가 무엇인지 알았으니 두 가지 수치 예를 사용하여 뉴턴의 이항 공식을 적용하는 방법을 살펴보겠습니다.

실시예 1

  • 뉴턴의 이항식을 적용하여 다음 이항식의 거듭제곱을 계산합니다.

(x+3)^2

분명히 이 이항식은 제곱이므로 주목할만한 항등식에 대한 공식( How to 풀기 주목할만한 항등식 )으로도 풀 수 있지만, 이항 정리를 예로 들어 계산하겠습니다.

우선 뉴턴의 이항 공식을 적용해야 합니다.

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

이 경우 n=2이므로 다음과 같습니다.

\left( x+3\right)^2 =\begin{pmatrix} 2 \\ 0 \end{pmatrix} \right)x^2 \cdot 3^0 + \begin{pmatrix} 2 \\ 1 \end{pmatrix} x^1\cdot3^1 + \begin{pmatrix} 2 \\ 2 \end{pmatrix} x^{0}\cdot3^{2}

잘 보세요. 처음에는 첫 번째 항(x)을 가능한 최대값(이 경우 2)으로 올립니다. 반면에 두 번째 항(3)을 가능한 최소값(항상 0)으로 올립니다. 오른쪽으로 갈수록 첫 번째 항은 이전보다 낮은 숫자로 , 두 번째 항은 이전보다 높은 숫자로 올려야 합니다.

이제 조합 숫자를 계산해 보겠습니다.

\left( x+3\right)^2 =1\cdot x^2\cdot 3^0 + 2\cdot x^1\cdot 3^1 + 1\cdot x^{0}\cdot 3^{2}

우리는 힘을 해결합니다:

\left( x+3\right)^2 =1\cdot x^2\cdot 1 + 2\cdot x\cdot 3 + 1\cdot 1\cdot 9

마지막으로 곱셈을 계산합니다.

\left( x+3\right)^2 =x^2 + 6x + 9

실시예 2

이제 조금 더 어려운 문제를 풀어보겠습니다.

  • 뉴턴의 이항식을 적용하여 다음 이항식의 거듭제곱을 구하세요.

(2x+1)^3

이항 정리의 공식은 다음과 같습니다.

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

이 경우 n=3이므로 다음과 같습니다.

\left( 2x+1\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)(2x)^3 \cdot 1^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^{2}\cdot 1^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^{1}\cdot 1^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^{0}\cdot 1^{3}

조합 숫자를 계산합니다.

\left( 2x+1\right)^3 =1\cdot (2x)^3 \cdot 1^0 + 3\cdot (2x)^{2}\cdot 1^1 + 3 \cdot (2x)^{1}\cdot 1^{2} + 1\cdot (2x)^{0}\cdot 1^{3}

이제 거듭제곱을 해결합니다. 이를 위해서는 다음 두 가지 속성을 기억하는 것이 중요합니다.

• 단항식을 지수로 올리면 계수와 변수도 같은 지수로 올라간다 →

(2x)^3=2^3\cdot x^3 =8\cdot x^3 =8x^3

• 0이 되는 항은 1 →

(2x)^0=1

따라서 우리는 다음 두 가지 속성을 통해 힘을 찾습니다.

\left( 2x+1\right)^3 =1\cdot 2^3x^3 \cdot 1 + 3\cdot 2^2x^{2}\cdot 1 + 3 \cdot 2^1x^{1}\cdot 1 + 1\cdot 1\cdot 1

\left( 2x+1\right)^3 =1\cdot 8x^3 \cdot 1 + 3\cdot 4x^{2}\cdot 1 + 3 \cdot 2x\cdot 1 + 1\cdot 1\cdot 1

마지막으로 항을 곱합니다.

\left( 2x+1\right)^3 =8x^3 + 12x^{2}+6x + 1

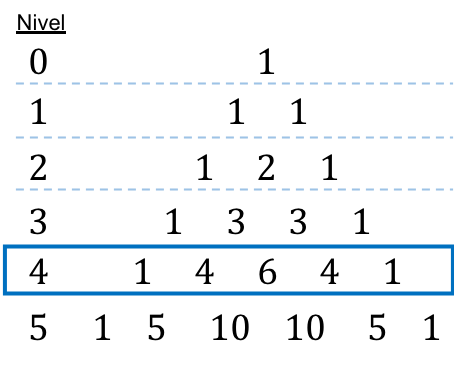
뉴턴의 이항식과 타르탈리아(또는 파스칼)의 삼각형

위의 예에서 보았듯이 조합수를 계산하는 것은 약간 지루합니다. 그렇기 때문에 조합수를 풀 필요가 없도록 트릭을 가르쳐 드리겠습니다. 파스칼의 삼각형이라고도 알려진 Tartaglia 삼각형을 사용하면 해당 조합의 가치가 얼마인지 직접 알 수 있기 때문입니다.

그것이 무엇인지 모르는 경우를 대비해 파스칼의 삼각형 이라고도 불리는 타르탈리아 삼각형은 삼각형 모양으로 배열된 숫자를 수학적으로 표현한 것입니다.

Tartaglia 또는 Pascal 삼각형을 구성하려면 항상 1인 삼각형의 꼭지점에서 시작해야 하며, 그런 다음 아래 선의 수가 결정됩니다. 다음 줄의 각 숫자는 항상 1인 줄의 끝을 제외하고 바로 위에 있는 두 숫자의 합과 같습니다.

뉴턴 쌍 1 고등학교 온라인

따라서 Tartaglia 삼각형의 각 숫자는 조합 숫자의 결과에 해당합니다. 다음 그림을 살펴보십시오.

예를 들어, 이항 계수

\begin{pmatrix} 3 \\ 1 \end{pmatrix}

Tartaglia 삼각형의 위치에 3이 있기 때문에 3과 동일합니다.

따라서 우리는 Tartaglia(또는 Pascal)의 삼각형을 사용하여 뉴턴의 이항식을 훨씬 더 빨리 풀 수 있습니다. 왜냐하면 조합수 계산을 생략할 수 있기 때문입니다.

예를 들어, 다음과 같은 이항식 전위화를 수행하려는 경우:

(x+5)^3

뉴턴의 이항 법칙을 적용하면 다음과 같은 대수식을 얻을 수 있습니다.

\left(x+5\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)x^3 \cdot 5^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 5^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 5^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 5^{3}

글쎄, 조합 수를 하나씩 계산하는 대신 각 조합 수를 해당 Tartaglia 삼각형의 계수로 간단히 대체할 수 있습니다. 이 경우 이항식은 3차로 올라가므로 삼각형의 세 번째 수준에 해당합니다.

Tartaglia 또는 Pascal의 삼각형과 Newton의 이항식

\left(x+5\right)^3 =\color{red} \bm{1} \color{black} \cdot x^3 \cdot 5^0 + \color{red} \bm{3} \color{black} \cdot x^{2}\cdot 5^1 + \color{red} \bm{3} \color{black} \cdot x^{1}\cdot 5^{2} +\color{red} \bm{1} \color{black} \cdot x^{0}\cdot 5^{3}

이제 우리가 해야 할 일은 나머지 작업을 수행하는 것입니다.

\left(x+5\right)^3 =1 \cdot x^3 \cdot 1 + 3\cdot x^{2}\cdot 5 + 3 \cdot x\cdot 25 +1\cdot 1\cdot 125

\left(x+5\right)^3 =x^3+ 15x^2 + 75x +125

보시다시피, Tartaglia(또는 Pascal)의 삼각형은 우리가 보여준 것처럼 더 간단하고 빠른 방법으로 뉴턴의 이항식을 계산하는 데 사용됩니다. 이것이 우리가 그것을 사용하는 것이 좋습니다 이유입니다.

지금까지 우리가 본 모든 것을 요약하기 위해 Tartaglia(또는 Pascal) 삼각형의 숫자를 사용한 뉴턴의 이항식 표현이 어떻게 보이는지 보여주는 이미지를 남겨드립니다.

뉴턴의 이항식과 파스칼의 삼각형 또는 타르탈리아

음의 뉴턴 이항식: 빼기의 힘

지금까지 우리가 풀었던 뉴턴 이항식의 모든 예는 덧셈이었습니다. 반면, 이항식의 두 항 중 하나가 음의 부호를 갖는 경우 절차는 유사하지만 약간 변경됩니다.

이항식의 항 중 하나가 음수인 경우, 즉 (ab) n 유형의 뺄셈인 경우 뉴턴 이항식의 전개 기호는 + – + – + – + – …

아래에서 우리는 이항 정리와 이미 존재하는 Tartaglia 삼각형의 계수를 사용하여 처음 5도의 음이항식의 거듭제곱을 개발했습니다. 따라서 필요한 이항식을 직접 찾을 수 있습니다.

음의 뉴턴 뺄셈의 이항 거듭제곱 2

뉴턴의 이항식의 속성

뉴턴의 이항식은 다음과 같은 특징을 가지고 있습니다.

  • 뉴턴의 이항식을 분해하면 항상 이항식의 차수보다 하나의 항이 더 많아집니다. 즉, 쌍을 위한 것입니다.

    (a+b)^n

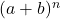
    그들은 영향을 받는다

    n+1

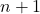
    자귀.

  • 요소의 힘

    a

    다음으로 시작

    n

    마지막 분기에는 0에 도달할 때까지 감소합니다.

  • 요소의 힘

    b

    그들은 다른 방향으로 갑니다: 0에서 시작하여 도달할 때까지 증가합니다.

    n

    마지막 학기에.

  • 뉴턴 이항식의 각 요소에 대해 지수의 합은 다음과 같습니다.

    a

    그리고

    b

    동일하다

    n.

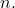
  • 뉴턴의 이항식의 첫 번째 항의 계수는 항상 1(양수)이고 두 번째 계수는 이항식의 지수(양수 또는 음수)와 같습니다.

뉴턴 이항식의 k번째 항을 계산합니다.

이는 드문 일이지만 뉴턴의 이항 전개를 하는 대신에 뉴턴의 이항식의 k번째 항, 즉 위치 k를 차지하는 항을 결정하라는 문제에 직면할 때도 있습니다.

따라서 뉴턴의 이항식에서 k 자리를 차지하는 항을 계산하려면 이항식이 덧셈인지 뺄셈인지에 따라 달라지는 공식을 사용해야 합니다.

  • 뉴턴의 이항식이 양수인 경우 k번째 항의 값은 다음 공식을 사용하여 계산됩니다.

(a+b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

  • 뉴턴의 이항식이 음수인 경우 k번째 항의 값은 다음 공식으로 결정됩니다.

(a-b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

예를 들어, 다음 5차 이항식의 네 번째 항을 찾습니다.

(x+3)^5

합계로 구성된 이항식이므로 첫 번째 공식을 적용합니다.

T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

수식의 변수를 해당 값으로 바꿉니다.

T_4 = \begin{pmatrix} 5 \\ 4-1 \end{pmatrix} x^{5-4+1}\cdot 3^{4-1}

그리고 우리는 다음 작업을 수행합니다.

T_4 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} x^{2}\cdot 3^{3}

T_4 = 10 \cdot x^{2}\cdot 27

T_4 = 270 x^{2}

그리고 이런 방식으로 우리는 다른 모든 항을 계산할 필요 없이 뉴턴의 이항 확장의 네 번째 항을 계산했습니다.

뉴턴의 이항식에 대한 해결된 연습문제

이제 이항 정리가 무엇인지 설명했으므로 연습할 수 있도록 뉴턴의 이항에 대한 몇 가지 단계별 연습 문제를 해결해 보겠습니다. 또한 의견에 질문이나 제안 사항을 남길 수 있다는 점을 기억하세요.

연습 1

이항 정리를 사용하여 다음 이항 거듭제곱을 확장합니다.

(x+4)^3

먼저 뉴턴의 이항 공식을 사용합니다.

\left(x+4\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} x^3 \cdot 4^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 4^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 4^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 4^{3}

이항식은 3의 거듭제곱이므로 조합수를 직접 찾기 위해 Tartaglia 삼각형의 세 번째 수준을 살펴봅니다.

뉴턴의 이항정리 연습문제를 단계별로 풀다 1 고등학교

(x+4)^3 = 1\cdot x^3 \cdot 4^0+3 \cdot x^2 \cdot 4^1 + 3 \cdot x^1 \cdot 4^2+1 \cdot x^0 \cdot 4^3

우리는 다음과 같은 권한을 수행합니다.

1\cdot x^3 \cdot 1 + 3 \cdot x^2 \cdot 4+ 3 \cdot x \cdot 16 +1 \cdot 1 \cdot 64

그리고 마지막으로 다음과 같이 곱합니다.

x^3 + 3x^2 \cdot 4 + 3 x \cdot 16 + 64

\bm{x^3 + 12x^2 + 48 x + 64}

연습 2

뉴턴의 이항식을 사용하여 다음과 같은 거듭제곱을 계산합니다.

(3x+2)^3

먼저 뉴턴의 이항 공식을 적용합니다.

\displaystyle \left(3x+2\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} (3x)^3 \cdot 2^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (3x)^{2}\cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (3x)^{1}\cdot 2^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (3x)^{0}\cdot 2^{3}

이항식은 세제곱이므로 조합수의 값을 직접 알기 위해 파스칼 삼각형의 세 번째 수준을 살펴보겠습니다.

뉴턴의 이항정리 연습문제를 단계별로 풀다 1 고등학교

\left(3x+2\right)^3 = 1\cdot (3x)^3 \cdot 2^0+3 \cdot (3x)^2 \cdot 2^1+ 3 \cdot (3x)^1 \cdot 2^2+1 \cdot (3x)^0 \cdot 2^3

우리는 단항식의 거듭제곱을 계산합니다.

1\cdot 27x^3 \cdot 1+ 3 \cdot 9x^2 \cdot 2+3 \cdot 3x \cdot 4 + 1 \cdot 1 \cdot 8

그리고 마지막으로 곱셈을 수행합니다.

27x^3 + 27x^2 \cdot 2 +9x \cdot 4+8

\bm{27x^3 + 54x^2 +36x+8}

연습 3

뉴턴의 이항식을 사용하여 다음 다항식을 확장합니다.

(2x-2)^3

먼저 뉴턴의 이항식을 사용합니다. 그러나 괄호 안에 뺄셈이 있으므로 각 항의 계수 부호를 번갈아 바꿔야 합니다.

(2x-2)^3=\begin{pmatrix} 3 \\ 0 \end{pmatrix} (2x)^3 \cdot 2^0-\begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^2 \cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^1 \cdot 2^2-\begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^0 \cdot 2^3

이항식은 3의 거듭제곱이므로 조합수를 직접 계산하기 위해 Tartaglia 삼각형의 세 번째 수준을 살펴보겠습니다.

뉴턴의 이항정리 연습문제를 단계별로 풀다 1 고등학교

(2x-2)^3=1\cdot (2x)^3 \cdot 2^0-3 \cdot (2x)^2 \cdot 2^1 + 3 \cdot (2x)^1 \cdot 2^2-1 \cdot (2x)^0 \cdot 2^3

우리는 다음과 같은 권한을 수행합니다.

1\cdot 8x^3 \cdot 1- 3 \cdot 4 x^2 \cdot 2+ 3 \cdot 2x \cdot 4-1 \cdot 1 \cdot 8

그리고 우리는 곱셈을 푼다:

8x^3 - 12 x^2 \cdot 2 +6x \cdot 4 -8

\bm{8x^3 -24 x^2 +24x -8}

연습 4

다음 공식을 사용하여 다음 뉴턴 이항식의 확장된 표현을 찾습니다.

(4x-3y)^4

뉴턴의 이항식에 대한 일반 공식을 적용해야 하지만 이 경우 괄호 안에 뺄셈이 있으므로 각 항의 부호를 번갈아 사용해야 합니다.

\begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}

이항식은 네 번째로 증가하므로 Tartaglia 삼각형의 레벨 4를 보고 조합 숫자를 직접 찾습니다.

뉴턴의 이항 피라미드

\begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}

우리는 모든 힘을 깨닫습니다:

1\cdot 256x^4 \cdot 1-4\cdot 64x^3 \cdot 3y+6 \cdot 16x^2 \cdot 9y^2 - 4 \cdot 4x \cdot 27y^3+1 \cdot 1 \cdot 81y^4

그리고 마지막으로 곱셈을 푼다.

256x^4-256x^3 \cdot 3y+96x^2 \cdot 9y^2 - 16x \cdot 27y^3+81y^4

\bm{256x^4-768x^3y+864x^2y^2-432xy^3+81y^4}

연습 5

다음 이항식의 전개에서 일곱 번째 항을 결정합니다.

(2x-5y)^{10}

음이항식이므로 다음 공식을 사용해야 합니다.

T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

우리는 항 7을 결정하고 이항식을 10의 거듭제곱으로 올리므로 해당 값을 공식에 대입하면 다음과 같습니다.

T_7= (-1)^{7-1} \begin{pmatrix} 10 \\ 7-1 \end{pmatrix} (2x)^{10-7+1} \cdot (5y)^{7-1}

따라서 다음 용어를 아는 것으로 충분합니다.

\begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}

뉴턴의 이항식의 역사

이항 정리의 기원은 영국의 유명한 과학자 아이작 뉴턴(1642-1727)에 기인하지만 실제로 이 정리의 첫 번째 공식은 1000년경 페르시아 엔지니어 알 카리지(Al-Karijí)에 의해 처음 발견되었습니다. 13세기에 중국 수학자 Yang Hui와 Chuh Shih-Chieh는 이미 작은 각도의 이항 확장을 알고 있었습니다.

이후 17세기에 뉴턴은 이전 수학자들이 마련한 기초 위에 이항 정리를 확장했습니다. 수학자 John Walls의 보간 및 외삽 방법과 일반화된 지수의 개념을 사용하여 그는 다항식을 무한 급수로 변환할 수 있었습니다.

1665년경 뉴턴은 이항 정리의 지수 n도 유리수일 수 있음을 증명하는 데 성공했습니다. 즉, 지수가 분수이면 이항식의 거듭제곱도 풀 수 있다는 것입니다. 반면에 음의 지수의 경우에도 증명되었습니다. 그리고 놀랍게도 그는 두 표현의 전개가 무한한 용어의 계열이라는 것을 발견했습니다.

이 발견으로 뉴턴은 무한 급수와 유한 다항식 사이의 관계에 의문을 제기하기 시작했고, 유한 다항식과 같은 방식으로 무한 급수를 사용하여 수학적 연산을 수행할 수 있다고 추론했습니다. 뉴턴은 이 정리를 발표한 적이 없지만 존 월스(John Walls)는 결국 1685년에 발표했고 뉴턴이 이 정리를 발견한 공로를 인정했습니다.

댓글 달기

이메일 주소는 공개되지 않습니다. 필수 필드는 *로 표시됩니다

Scroll to Top