이차 방정식 또는 이차 방정식은 항 중 하나의 최대 지수가 2인 2차 방정식입니다. 이는 방정식이 고유한 해 또는 해를 가질 수도 있지만 최대 두 개의 서로 다른 해를 가질 수 있음을 의미합니다. 전혀.
이차 방정식의 해 또는 근을 계산하려면 두 가지 다른 절차를 따를 수 있습니다: 이차 공식을 사용하거나 표현식을 인수분해합니다 . 이 기사에서는 두 가지 방법에 대해 설명하고 몇 가지 실제 연습을 제공합니다. 전체 설명이 매우 잘 이해되고 읽기를 최대한 활용할 수 있도록 몇 가지 개념을 명확히 하기 전에.
이차 방정식의 유형
이차 방정식 간의 주요 분류는 표현식 자체의 구조를 기반으로 합니다. 따라서 이러한 표현식의 표준 또는 일반적인 구조는 다음과 같습니다: ax² + bx + c . 이 공통 형식은 완전한 방정식과 동일하지만 null 또는 null 항이 있는 경우 구조가 달라질 수 있으며, 여기서 불완전한 방정식이 나타납니다. 다음으로 모든 유형의 특징에 대해 좀 더 자세히 설명하겠습니다.
완전한 이차 방정식
우리가 이미 말했듯이, 우리는 완전한 이차 방정식을 가지고 있습니다. 이 방정식은 모든 계수 a, b 및 c가 0이 아닙니다. 따라서 표현식은 문자에 대해 ax² + bx + c 구조를 따릅니다. 왜냐하면 이차 항, 선형 항 및 독립 항과 같은 모든 항을 갖기 때문입니다. 이 유형의 예는 다음 방정식입니다: x² + 2x + 1 = 0.
불완전한 이차 방정식
불완전한 방정식의 경우 어떤 계수가 0인지에 따라 구별할 수 있습니다. 이 설명으로 의심이 해결되지 않으면 바로 아래에서 단계별로 설명된 모든 사례를 찾을 수 있는 이미지를 참조하세요.
- 불완전 방정식(b = 0): 이 첫 번째 상황에서 우리는 다음 구조를 따르는 표현식을 찾습니다: ax² + c = 0. 이를 통해 우리는 두 가지 결과를 얻습니다: 분수 c/a의 근의 음수와 양수 .
- 불완전 방정식(c = 0): ax² + bx = 0 형식을 가질 때 방정식을 인수분해하여 x(ax + b) = 0이라는 표현식을 가져야 합니다. 따라서 x = 0 및 x = -라는 두 가지 해를 갖게 됩니다. b/a.
- 불완전 방정식(b = c = 0): 이 경우 방정식 ax² = 0이 있고 가능한 해는 x = 0 하나만 있습니다.
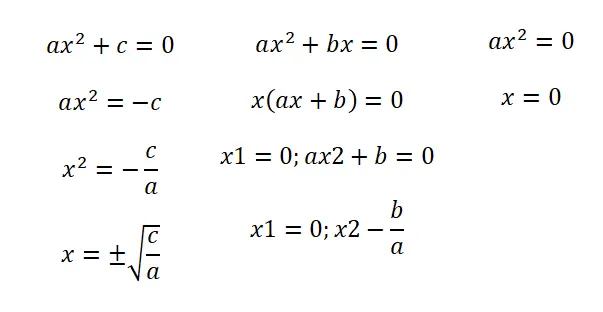
우리가 가르친 절차를 사용하면 불완전한 방정식을 풀 때 더 빨리 풀 수 있다는 점은 언급할 가치가 있습니다. 그러나 모든 경우에 우리가 아래에서 가르칠 2차 공식을 사용할 수 있으며, 존재하지 않는 계수에는 0만 쓰면 됩니다.
이차 방정식의 공식
2차 방정식(ax² + bx + c = 0)을 풀려면 일반 공식이나 2차 공식을 적용한 다음 수식의 각 문자에 해당하는 수치 값을 대입 해야 합니다.
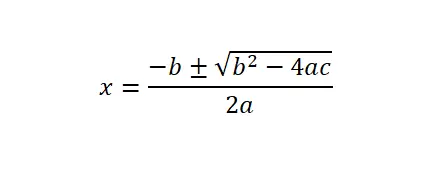
또한 판별식(Δ)이 b² – 4ac라는 표현으로 제곱근 아래에 위치한다는 점을 설명하는 것이 중요합니다. 이 수학적 개념으로부터 우리는 이 이차 방정식이 얼마나 많은 해를 가지고 있는지 알 수 있습니다. 기본적으로 세 가지 옵션이 있습니다. 판별식이 음수(실제 해가 없음), 판별식이 0(해가 하나만 있음) 또는 판별식이 양수(해가 두 개 있음)입니다.
완전한 이차 방정식 풀이의 예
다음 이차 방정식을 풀어보세요: 2x²+4x-6=0 그리고 아래 방정식으로 결과를 확인하세요. 다음 절차를 따르는 것이 좋습니다. 방정식 유형을 분석하고(0항 식별), 판별식을 계산하여 기존 해의 수를 알고, 마지막으로 공식을 사용하여 제안된 방정식을 푸는 것입니다.
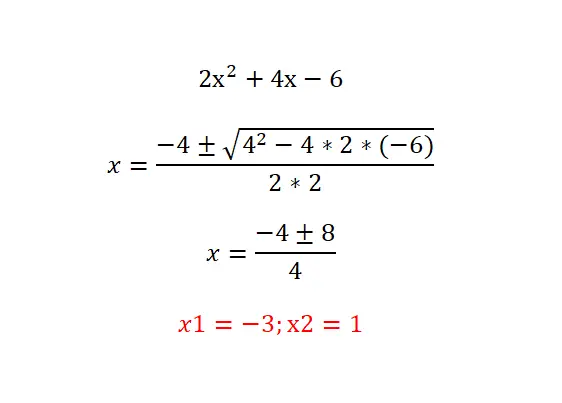
계승 이차 방정식
이차 방정식을 푸는 두 번째 방법은 인수분해 입니다. 따라서 다항식(우리의 경우에는 2차 다항식)을 인수분해하기 위해 다양한 방법을 사용할 수 있습니다. 일반적으로 이러한 스타일의 방정식의 경우 일반적으로 공통 용어로 인수분해됩니다. 그렇지 않은 경우 Notable Identities 를 적용해 볼 수 있지만 일반적으로 이러한 상황에서는 다른 방법을 알 필요가 없습니다.
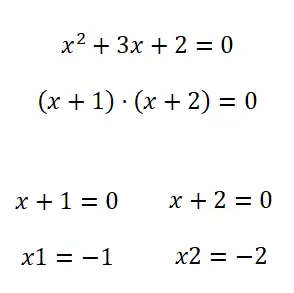
해를 이용한 이차방정식 연습
아래에서는 완전 및 불완전 이차 방정식 에 대한 일련의 연습을 찾을 수 있습니다. 이렇게 하면 이 기사 전반에 걸쳐 설명된 모든 이론을 검토하고 이를 연습에 적용하는 방법이 더 명확해질 것입니다. 스스로 해결해 보시고, 문제를 완료했거나 막히는 경우에만 해결책을 살펴보시기를 권장합니다. 즉, 이제 연습문제를 풀 수 있습니다.
연습 1
다음 이차 방정식을 푼다:
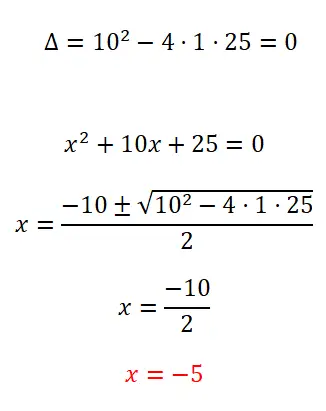
- 가능한 해의 수를 알기 위해 판별식을 계산하는 것부터 시작합니다.
- 이는 완전한 이차방정식이므로 이차방정식을 적용하여 계산을 푼다.
- 우리는 알려지지 않은 x의 값을 얻습니다.
연습 2
다음 이차 방정식을 푼다:
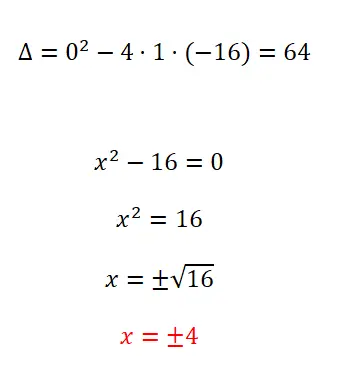
- 판별식을 계산하는 것부터 시작합니다.
- b = 0인 불완전한 이차 방정식이 있으므로 이 유형의 방정식에 대한 표준을 적용합니다.
- 결과를 얻기 위해 계산을 풀고 ± 기호를 잊을 수 없습니다.
연습 3
다음의 순서가 없는 이차 방정식을 풀어보세요:
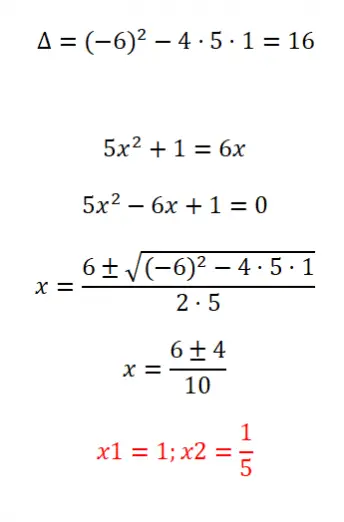
- 방정식의 판별식을 계산하는 것부터 시작합니다.
- 공식을 적용하기 전에 ax² + bx + c = 0 구조에 따라 방정식의 순서를 지정해야 합니다.
- 그런 다음 일반 공식을 적용합니다.
- 그리고 마침내 우리는 결과를 얻습니다.
연습 4
인수분해를 통해 다음 이차 방정식을 푼다:
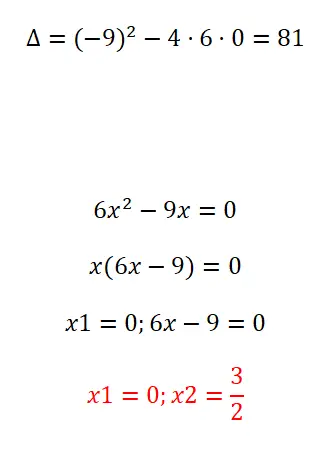
- 먼저 판별식을 계산합니다.
- 다음으로 x의 공통인수를 추출합니다.
- 따라서 첫 번째 해는 x = 0입니다.
- 그리고 두 번째는 x = 3/2입니다.
연습 5
아래에 표시된 완전한 이차 방정식을 풀어보세요.
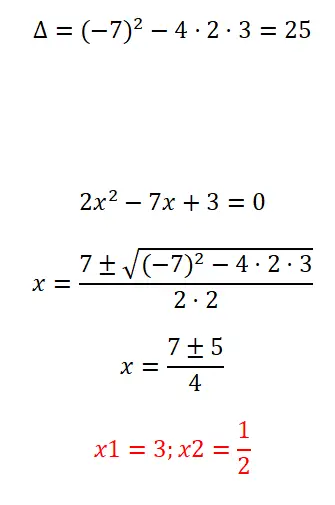
- 항상 그렇듯이, 문제의 방정식에 몇 개의 해가 있는지 알아내기 위해 판별식을 계산합니다.
- 다음으로 완전한 방정식이므로 이차 공식을 적용합니다.
- 마지막으로 방정식의 결과를 표현합니다.
연습 6
우리가 제공하는 분수로 이차 방정식을 풀어보세요:
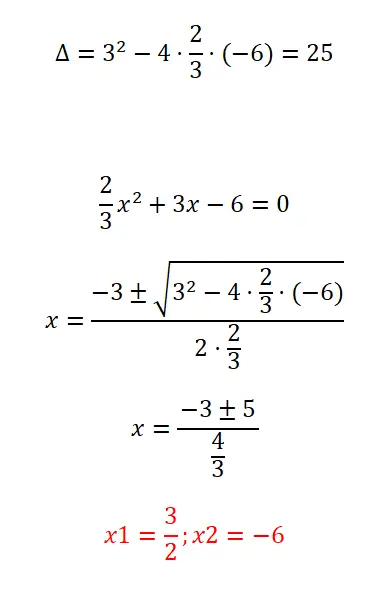
- 표현식의 판별식을 계산하는 것부터 시작합니다.
- 다음으로 계수 “a”가 분수로 구성된다는 점을 고려하여 이차 공식을 적용합니다.
- 우리는 계산을 해결합니다.
- 그리고 우리는 이미 방정식의 두 가지 근을 갖고 있습니다.
연습 7
다음 이차 방정식을 푼다:
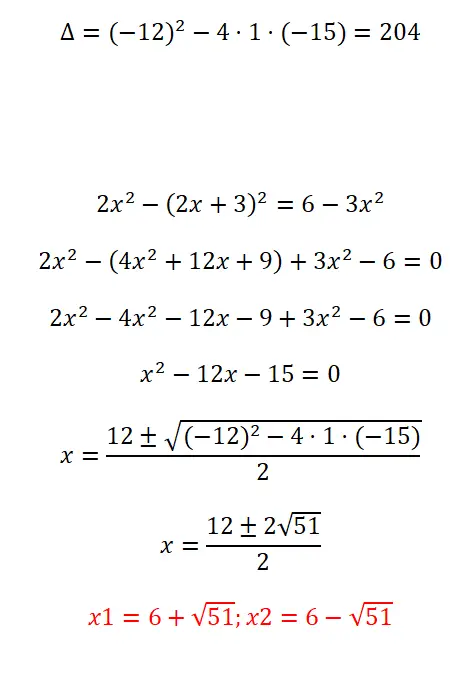
- 판별식을 계산하는 것부터 시작합니다.
- 공식을 적용하기 전에 식을 단순화하고 ax² + b + c = 0 형식을 제공해야 합니다.
- 공식의 모든 계수를 대체하고 계산을 해결합니다.
- 마침내 우리는 결과를 얻습니다.
연습 8
다음 이차 방정식의 풀이 증명:
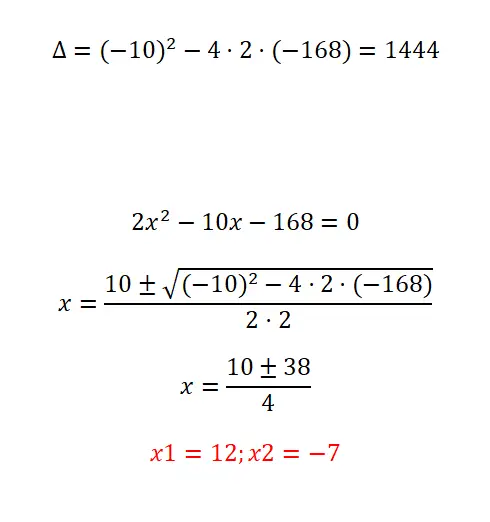
- 판별식을 계산하는 것부터 시작합니다.
- 보시다시피, 이것은 꽤 큰 계수를 가지고 있지만 간단한 이차 방정식입니다. 그러므로 우리는 공식을 적용하고 연산을 수행할 때 주의해야 합니다.
- 결국 우리는 가능한 두 가지 해결책을 모두 얻습니다.