유리수가 다른 숫자와 어떻게 다른지 궁금한 적이 있습니까? 이 글에서는 유리수의 고유한 특성과 분류를 포함하여 유리수의 깊이를 살펴보겠습니다. 개념을 더 잘 이해할 준비를 하세요!
유리수란 무엇입니까?
유리수(ℚ)는 분수로 표현될 수 있는 모든 숫자를 포함하는 실수 의 하위 클래스입니다. 이는 유리수란 두 정수의 비율인 a/b(여기서 b ≠ 0)로 쓸 수 있는 숫자라는 것을 의미합니다.
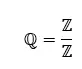
유리수는 일련의 반복되는 숫자로 구성되기 때문에 반복 또는 유한 소수로 표현될 수도 있습니다. 유리수의 예로는 1/2, 3/4, 10/3, 2/3 및 π(pi)가 있습니다.
합리성의 부분집합
유리수는 두 가지 하위 집합 으로 나눌 수 있습니다.
- 0, 모든 자연수, 모든 음수를 포함하는 정수입니다 .
- 십진수 또는 분수는 정수 부분과 소수 부분으로 구성된 값을 표현하는 모든 숫자로, 후자는 1보다 작은 값을 표현할 수 있습니다.

실수 집합의 또 다른 하위 범주는 좀 더 복잡한 무리수 입니다.
유리수의 예
유리수는 분수, 즉 두 정수의 몫으로 표현될 수 있는 숫자입니다. 다음은 유리수의 몇 가지 예입니다.
-23
-4/5
-1/2
-7/9
정수를 나타내는 모든 분수는 동일하게 유리수입니다. 예를 들어:
-1/1
-2/2
-3/3
유리수의 속성
유리수의 주요 특징은 항상 0이 아닌 분모를 갖는다는 것입니다.
이 집합의 두 번째 속성은 각각의 유리수는 등가 분수의 무한대로 표현될 수 있다는 것입니다. 예를 들어, 7/2와 같은 유리수 3.5는 14/4, 28/8… 및 기타 분수의 무한대로 쓸 수도 있습니다.
유리수는 분배 법칙도 만족합니다. 이는 한 분수를 다른 분수로 곱하거나 나누어도 결과에 영향을 미치지 않음을 의미합니다.
(a/b) (c/d) = (ac)/(bd)
(a/b)/(c/d) = (ad)/(bc)
유리수의 표현
유리수는 여러 가지 방법으로 표현할 수 있지만 가장 일반적인 방법은 분수 입니다. 분수는 분자와 분모라는 두 개의 숫자로 구성됩니다.
분자는 전체에서 고려되는 부분의 수를 나타내고, 분모는 전체에서 동일한 부분의 수를 나타냅니다. 예를 들어, 케이크를 8개의 동일한 조각으로 나누고 그 중 3개의 조각을 먹는다면, 먹은 케이크의 양을 나타내는 분수는 3/8이 됩니다.
유리수를 표현하는 또 다른 방법은 소수를 사용하는 것 입니다. 소수는 분모가 10, 100, 1000 등의 숫자인 분수를 나타내는 간단한 방법입니다. 예를 들어, 파이가 1/4이라면 이는 0.25(“전체가 0이고 25/100”임을 의미)로 표현할 수 있습니다.
하지만 그래픽으로 표현하려면 숫자의 순서가 잘 보이는 수직선 에 쓸 수도 있습니다. 다음으로 다음 줄의 예를 보여드리겠습니다.
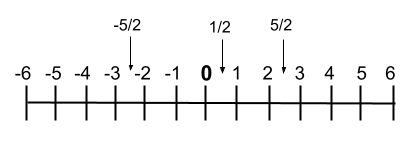
합리적인 운영
유리수의 기본 연산은 정수의 연산과 동일합니다: 덧셈, 뺄셈, 곱셈, 나눗셈. 이러한 유형의 연산을 해결하는 방법을 배우려면 분수 연산 에 대한 기사를 읽는 것이 좋습니다.
그러나 소수 밑이 있는 유리수로 작업하는 경우 소수 값을 처리할 때 사용하는 연산을 풀기 위한 절차를 따라야 합니다.
유리수 집합에 대한 결론
이 철저한 설명 후에 우리는 유리수 집합이 수학에서 가장 중요한 것 중 하나라는 결론을 내릴 수 있습니다. 여기에는 분수로 표현할 수 있는 모든 숫자가 포함되어 있어 수량을 매우 정확하게 표현할 수 있습니다.