가우스 방법 – 요르단

이 페이지에서는 Gauss-Jordan 방법이 무엇인지, Gauss 방법을 사용하여 방정식 시스템을 푸는 방법을 배웁니다. 또한, 가우스법을 적용한 시스템의 예제와 해결 연습문제도 함께 제공하므로 완벽하게 연습하고 이해할 수 있습니다.

가우스의 방법은 무엇입니까?

Gauss-Jordan 방법은 3개의 미지수를 갖는 방정식 시스템을 해결하는 데 사용되는 절차입니다. 즉, 다음과 같습니다.

$\left. \begin{array}{r} 3x-4y+5z=10 \\[2ex] x+5y-2z=4 \\[2ex] -x+4y+2z=-1 \end{array} \right\}$

가우스 방법의 목적은 초기 방정식 시스템을 계단식 시스템 , 즉 각 방정식이 이전 방정식보다 알려지지 않은 것이 하나 적은 시스템으로 변환하는 것입니다.

$\left. \begin{array}{r} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{array} \right\} \ \bm{\longrightarrow} \left. \begin{array}{r} A_1x+B_1y+C_1z=D_1 \\[2ex] B_2y+C_2z=D_2 \\[2ex] C_3z=D_3 \end{array} \right\}$

그러나 이렇게 하려면 먼저 연립방정식을 행렬 형식으로 표현하는 방법과 이 행렬에 허용되는 변환을 알아야 합니다. 그래서 이 두 가지에 대해서는 앞서 설명을 드리고, 이어서 가우스법 절차를 어떻게 활용하는지 알아보겠습니다.

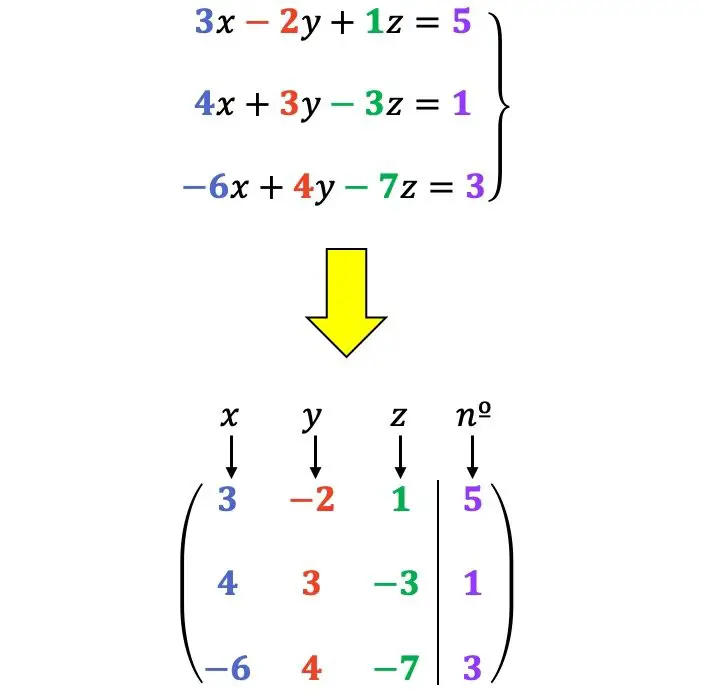
시스템 확장 매트릭스

시스템이 어떻게 해결되는지 보기 전에 방정식 시스템이 행렬 형태로 표현될 수 있다는 것을 알아야 합니다.

$x}$

첫 번째 열에 배치되며, 계수는

$y}$

두 번째 열에는 계수

$z$

세 번째 열에는 알 수 없는 숫자가 있고 네 번째 열에는 숫자가 있습니다.

예를 들어:

허용되는 행 변환

방정식 시스템을 스케일링된 시스템으로 변환하기 위해 시스템과 연관된 행렬에 대해 다음 작업 중 하나를 수행할 수 있습니다.

행렬의 행 순서를 변경합니다 .

예를 들어, 행렬의 라인 2와 3의 순서를 변경할 수 있습니다.

$\left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] -2 & 4 & -1 & 2 \\[2ex] 6 & 1 & -3 & 10 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] 6 & 1 & -3 & 10 \\[2ex] -2 & 4 & -1 & 2 \end{array} \right)$

행의 모든 항에 0이 아닌 숫자를 곱하거나 나눕니다 .

예를 들어, 라인 1을 4로 곱하고 라인 3을 2로 나눌 수 있습니다.

$\left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 2 & -4 & -2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc|c} 4 & -8 & 12 & 4 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 1 & -2 & -1 & 3 \end{array} \right)$

행을 동일한 행과 다른 행의 합에 숫자를 곱한 값으로 바꿉니다 .

예를 들어, 다음 행렬에서는 2행을 3행에 더하고 1을 곱합니다.

$\left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 2 & 4 & 1 & -5 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1 \cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 3 & 2 & 4 & -6 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right)$

가우스 방법을 사용하여 방정식 시스템을 푸는 방법은 무엇입니까?

이제 가우스 방법을 사용하여 방정식 시스템을 해결하는 절차를 예를 통해 살펴보겠습니다.

$\left. \begin{array}{r} -x+2y+2z=-24 \\[2ex] x+y+z=48 \\[2ex] 2x-6y+4z=12 \end{array} \right\}$

가장 먼저 해야 할 일은 시스템의 확장 행렬 입니다.

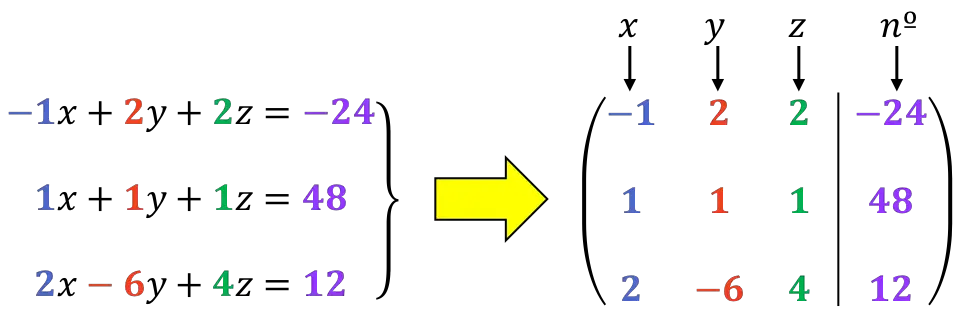
나중에 살펴보겠지만 첫 번째 줄의 첫 번째 숫자는 1인 것이 더 좋습니다. 따라서 줄 1과 2의 순서를 변경하겠습니다.

$\left( \begin{array}{ccc|c} -1 & 2 & 2 &-24 \\[2ex] 1 & 1 & 1 & 48 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \xrightarrow{ f_1 \rightarrow f_2} \\[2ex] \xrightarrow{ f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} \color{blue}\boxed{\color{black}1} & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 &-24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

가우스 방법의 목표는 주대각선 아래의 숫자를 0으로 만드는 것입니다. 즉, 빨간색 숫자를 0으로 변환해야 합니다.

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{red}\bm{-1} & 2 & 2 &-24 \\[2ex] \color{red}\bm{2} & \color{red}\bm{-6} & 4 & 12 \end{array} \right)$

이러한 숫자를 제거하려면 행을 적절하게 변환해야 합니다.

예를 들어, 두 번째 행의 첫 번째 요소인 -1은 첫 번째 행의 첫 번째 요소인 1의 음수입니다. 따라서 첫 번째 줄을 두 번째 줄에 추가하면 -1이 제거됩니다.

$\begin{array}{lccc|c} & -1 & 2 & 2 & -24 \\ + & \phantom{-}1 & 1 & 1 & \phantom{-}48 \\ \hline & \phantom{-}0 & 3 & 3 & \phantom{-}24 \end{array} \begin{array}{l} \color{blue}\bm{\leftarrow f_2} \\ \color{blue}\bm{\leftarrow f_1} \\ \phantom{hline} \\ \end{array}$

따라서 이 합을 계산하면 다음 행렬이 됩니다.

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 & -24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{blue}\boxed{\color{black}0} & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)$

이런 식으로 우리는 -1을 0으로 변환했습니다.

이제 우리는 2를 변환할 것입니다. 눈치채셨겠지만, 세 번째 행의 첫 번째 요소인 2는 첫 번째 행의 첫 번째 요소인 1의 두 배입니다. 따라서 첫 번째 행에 -2를 곱한 값을 세 번째 행에 추가하면 2가 제거됩니다.

$\begin{array}{lccc|c} & \phantom{-}2 & -6 & \phantom{-}4 & \phantom{-}12 \\ + & -2 & -2 & -2 & -96 \\ \hline & \phantom{-}0 & -8 & \phantom{-}2 & -84 \end{array} \begin{array}{l} \color{blue} \bm{\leftarrow f_3} \\ \color{blue} \bm{\leftarrow -2 f_1} \\ \phantom{hline} \\ \end{array}$

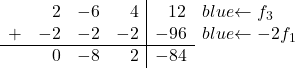
따라서 우리는 다음 매트릭스로 끝납니다.

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] \color{blue}\boxed{\color{black}0} & -8 & 2 & -84 \end{array} \right)$

이런 식으로 우리는 2를 0으로 변환했습니다.

이제 우리가 해야 할 일은 -8을 0으로 변환하는 것뿐입니다. 이를 위해 세 번째 줄에 3을 곱하고 두 번째 줄에 8을 곱합니다.

$\begin{array}{lccc|r} & 0 & -24 & \phantom{2}6 & -252 \\ + & 0 & \phantom{-}24 & 24 & \phantom{-}192 \\ \hline & 0 & \phantom{-2}0 & 30 & -60 \end{array} \begin{array}{l}\color{blue}\bm{ \leftarrow 3f_3} \\\color{blue}\bm{ \leftarrow 8f_2} \\ \phantom{hline} \\ \end{array}$

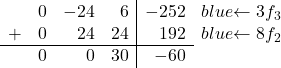
따라서 우리는 다음 행렬을 얻습니다.

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & -8 & 2 & -84 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3f_3 + 8f_2} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & 30 & -60 \end{array} \right)$

그리고 이러한 변환을 통해 주대각선 아래의 모든 숫자는 0이 됩니다. 이제 방정식 시스템을 풀 수 있습니다.

이제 행렬을 미지수가 있는 방정식 시스템으로 변환 해야 합니다. 이렇게 하려면 첫 번째 열이

$x$

, 의 두 번째 열

$y$

, 의 세 번째 열

$z$

마지막 열은 알 수 없는 숫자입니다.

$\left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & 0 & 30 & -60 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x+1y+1z=48 \\[2ex] 3y+3z=24 \\[2ex] 30z=-60 \end{array} \right\}$

그리고 마지막으로 시스템을 풀려면 방정식의 미지수를 아래에서 위로 풀어야 합니다. 마지막 방정식에는 미지수가 하나만 있으므로 이를 풀고 그 값을 찾을 수 있습니다.

$30z=-60$

$z = \cfrac{-60}{30}$

$\bm{z=-2}$

이제 z가 무엇인지 알았으므로 그 값을 두 번째 방정식에 대입하면 다음 값을 찾을 수 있습니다.

$y$

$3y+3z=24 \ \xrightarrow{z \ = \ -2} \ 3y+3(-2)=24$

$3y-6=24$

$3y=24+6$

$3y=30$

$y=\cfrac{30}{3}$

$\bm{y=10}$

그리고 첫 번째 방정식에서도 동일한 작업을 수행합니다. 다른 미지수의 값을 대체하고 지웁니다.

$x$

$1x+1y+1z=48 \ \xrightarrow{y \ = \ 10 \ ; \ z \ = \ -2} \ 1x+1(10)+1(-2)=48$

$x+10-2=48$

$x=48-10+2$

$\bm{x=40}$

따라서 연립방정식의 해는 다음과 같습니다.

$\bm{x=40} \quad \bm{y=10} \quad \bm{z=-2}$

Gauss-Jordan 방법으로 방정식 시스템의 문제를 해결했습니다.

연습 1

가우스 방법을 사용하여 다음 방정식 시스템을 풉니다.

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\}$

해결책 보기

우리가 가장 먼저 해야 할 일은 시스템의 확장된 매트릭스입니다.

$\left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right)$

이제 기본 배열 아래의 모든 숫자를 0으로 만들어야 합니다.

따라서 첫 번째 열의 마지막 두 항을 취소하기 위해 행 연산을 수행합니다.

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3-2f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right)$

이제 두 번째 열에서 마지막 요소를 제거합니다.

$\left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right)$

주대각선 아래의 모든 숫자가 0이 되면 이제 방정식 시스템을 풀 수 있습니다. 이를 위해 우리는 미지수를 갖는 방정식 시스템의 형태로 행렬을 다시 표현합니다.

$\left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y-z=2 \\[2ex] -3y+4z=-2 \\[2ex] 1z=1 \end{array} \right\}$

그리고 방정식의 미지수를 아래에서 위로 해결합니다. 먼저 마지막 방정식을 푼다.

$1z= 1$

$z=\bm{1}$

이제 z 값을 두 번째 방정식에 대입하여 y 값을 찾습니다.

$-3y+4z=-2 \ \xrightarrow{z \ = \ 1} \ -3y+4(1)=-2$

$-3y+4=-2$

$-3y=-2-4$

$-3y=-6$

$y=\cfrac{-6}{-3} = \bm{2}$

그리고 우리는 첫 번째 방정식에서도 동일한 작업을 수행합니다. 다른 미지수의 값을 대체하고 x를 해결합니다.

$x+y-z=2 \ \xrightarrow{y \ = \ 2 \ ; \ z \ = \ 1} \ x+(2)-(1)=2$

$x+1=2$

$x=2-1$

$\bm{x=1}$

따라서 연립방정식의 해는 다음과 같습니다.

$\bm{x=1} \qquad \bm{y=2} \qquad \bm{z=1}$

연습 2

가우스 방법을 사용하여 다음 방정식 시스템의 해를 구합니다.

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\}$

해결책 보기

우리가 가장 먼저 해야 할 일은 시스템의 확장된 매트릭스입니다.

$\left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right)$

가우스 방법을 적용하려면 첫 번째 줄의 첫 번째 숫자가 1이면 더 간단합니다. 따라서 줄 1과 2의 순서를 변경합니다.

$\left( \begin{array}{ccc|c}2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1\rightarrow f_2} \\[2ex] \xrightarrow{f_2\rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1\end{array} \right)$

이제 기본 배열 아래의 모든 숫자를 0으로 만들어야 합니다.

따라서 첫 번째 열의 마지막 두 요소를 바꾸기 위해 행 작업을 수행합니다.

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] \xrightarrow{f_3-4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21 \end{array} \right)$

이제 두 번째 열의 마지막 요소를 0으로 변환합니다.

$\left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right)$

주대각선 아래의 모든 숫자가 0이 되면 방정식 시스템을 풀 수 있습니다. 이를 위해 우리는 미지수를 갖는 방정식 시스템의 형태로 행렬을 다시 표현합니다.

$\left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+2z=5 \\[2ex] -5y-2z=-13 \\[2ex] -5z=5 \end{array} \right\}$

그리고 방정식의 미지수를 아래에서 위로 해결합니다. 먼저 마지막 방정식을 푼다.

$-5z= 5$

$z=\cfrac{5}{-5}=\bm{-1}$

이제 z 값을 두 번째 방정식에 대입하여 y 값을 찾습니다.

$-5y-2z=-13 \ \xrightarrow{z \ = \ -1} \ -5y-2(-1)=-13$

$-5y+2=-13$

$-5y=-13-2$

$-5y=-15$

$y=\cfrac{-15}{-5} = \bm{3}$

그리고 우리는 첫 번째 방정식에서도 동일한 작업을 수행합니다. 다른 미지수의 값을 대체하고 x를 해결합니다.

$x+3y+2z=5 \ \xrightarrow{y \ = \ 3 \ ; \ z \ = \ -1} \ x+3(3)+2(-1)=5$

$x+9-2=5$

$x=5-9+2$

$\bm{x=-2}$

따라서 연립방정식의 해는 다음과 같습니다.

$\bm{x=-2} \qquad \bm{y=3} \qquad \bm{z=-1}$

연습 3

가우스 방법을 사용하여 다음 방정식 시스템의 해를 계산합니다.

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5 \end{array} \right\}$

해결책 보기

우리가 가장 먼저 해야 할 일은 시스템의 확장된 매트릭스입니다.

$\left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5 \end{array} \right)$

이제 상위 배열 아래의 모든 숫자를 0으로 만들어야 합니다.

따라서 첫 번째 열의 마지막 두 요소를 바꾸기 위해 행 작업을 수행합니다.

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+2f_1} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right)$

이제 두 번째 열의 마지막 요소를 0으로 변환합니다.

$\left( \begin{array}{ccc|c}2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+8f_2} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39 \end{array} \right)$

$\left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39\end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 2x+3y+1z=-1 \\[2ex] -5y+z=3 \\[2ex] 13z=39 \end{array} \right\}$

그리고 방정식의 미지수를 아래에서 위로 해결합니다. 먼저 마지막 방정식을 푼다.

$13z= 39$

$z=\cfrac{39}{13}=\bm{3}$

이제 z 값을 두 번째 방정식에 대입하여 y 값을 찾습니다.

$-5y+z=3 \ \xrightarrow{z \ = \ 3} \ -5y+(3)=3$

$-5y=3-3$

$-5y=0$

$y=\cfrac{0}{-5} = \bm{0}$

그리고 우리는 첫 번째 방정식에서도 동일한 작업을 수행합니다. 다른 미지수의 값을 대체하고 x를 해결합니다.

$2x+3y+1z=-1 \ \xrightarrow{y \ = \ 0 \ ; \ z \ = \ 3} \ 2x+3(0)+1(3)=-1$

$2x+0+3=-1$

$2x=-1-3$

$2x=-4$

$x=\cfrac{-4}{2}=\bm{-2}$

따라서 연립방정식의 해는 다음과 같습니다.

$\bm{x=-2} \qquad \bm{y=0} \qquad \bm{z=3}$

연습 4

가우스 방법을 사용하여 3개의 미지수가 있는 다음 방정식 시스템을 풉니다.

$\left. \begin{array}{r} 2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\}$

해결책 보기

가우스 방법을 적용하기 전에 모든 미지수가 방정식 왼쪽에 있고 숫자가 오른쪽에 있도록 방정식 시스템을 배열해야 합니다.

$\left. \begin{array}{r}2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\} \longrightarrow \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6\end{array} \right\}$

시스템이 주문되면 개발된 시스템 매트릭스를 구성합니다.

$\left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right)$

첫 번째 행의 모든 숫자는 짝수이므로 행을 처리하기 전에 첫 번째 행을 2로 나눕니다. 이렇게 하면 계산이 더 쉬워집니다.

$\left( \begin{array}{ccc|c}2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1/2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6\end{array} \right)$

이제 기본 배열 아래의 모든 숫자를 0으로 만들어야 합니다.

따라서 첫 번째 열의 마지막 두 요소를 바꾸기 위해 행 작업을 수행합니다.

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18\end{array} \right)$

이전과 마찬가지로 마지막 줄의 모든 숫자는 9의 배수이므로 계산을 더 쉽게 하기 위해 9로 나눕니다.

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex]\xrightarrow{f_3/9} & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right)$

이제 두 번째 열의 마지막 요소를 0으로 변환합니다.

$\left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right)$

$\left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x-2y-3z=3 \\[2ex] 5y+6z=-8 \\[2ex] 1z=2 \end{array} \right\}$