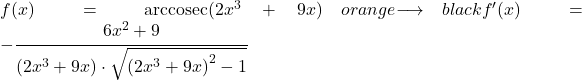코시컨트 호의 미분

이 페이지에서는 역코시컨트의 미분 공식이 무엇인지 볼 수 있습니다. 또한, 함수의 코시컨트 도함수에 대한 해결된 연습 문제를 볼 수 있습니다.

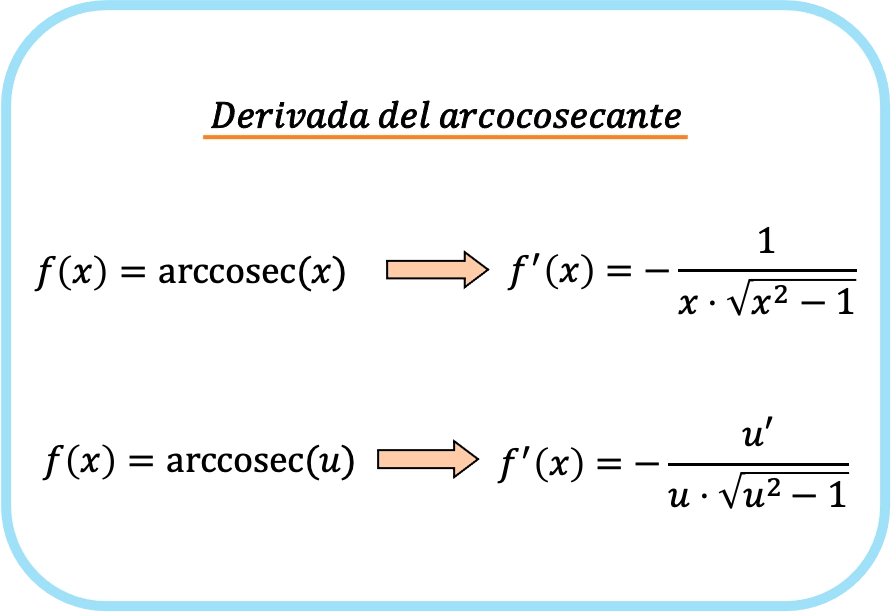
Arccosecant 파생 공식

x의 역코시컨트의 미분은 x 곱하기 x 제곱근 – 1의 곱에 대한 음의 1입니다.

f(x)=\text{arccosec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{x\cdot \sqrt{x^2-1}}

따라서 함수의 역코시컨트의 도함수는 해당 함수의 도함수의 몫을 함수로 나눈 값에 해당 함수의 근을 곱한 값의 제곱 빼기 1과 같습니다.

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

사실 앞의 두 수식은 동일하지만, 두 번째 수식에서는 연쇄법칙이 적용됩니다. 실제로 항등함수 x를 u에 대입하면 x의 도함수가 1이므로 x의 역코시컨트의 도함수를 얻게 됩니다.

역코시컨트 파생 공식

여러분도 잘 아시는 바와 같이, 역코시컨트는 코시컨트의 역삼각 함수이지만, 그 도함수는 상당히 다릅니다. 다음 링크에서 다른 유형의 삼각 함수에 대한 공식을 볼 수 있습니다.

➤ 참조: 코시컨트의 도함수

코시컨트 호의 도함수 예

역코시컨트 도함수 규칙이 무엇인지 살펴보고, 다음으로 이러한 유형의 도함수에 대한 두 가지 예를 풀어보겠습니다. 하지만 코시컨트 호를 도출하는 방법에 대해 여전히 궁금한 점이 있으면 댓글로 문의해 주세요.

실시예 1

이 예에서는 이차 함수 x 2 의 역 코시컨트의 도함수가 얼마나 되는지 살펴보겠습니다.

f(x)=\text{arccosec}(x^2)

x 제곱의 역코시컨트 도함수를 계산하기 위해 위에서 본 공식을 적용합니다.

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

x의 2제곱 미분은 2x이므로 복합 함수의 미분은 다음과 같습니다.

f(x)=\text{arccosec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{x^2\cdot \sqrt{\left(x^2\right)^2-1}}=-\cfrac{2x}{x^2\cdot \sqrt{x^4-1}}

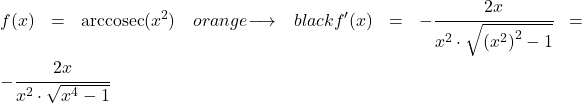
실시예 2

이 두 번째 예에서는 전위 함수의 역코시컨트를 유도합니다.

f(x)=\text{arccosec}(2x^3+9x)

전체 함수의 도함수를 찾으려면 역시선 도함수 규칙을 사용해야 합니다.

f(x)=\text{arccosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{u\cdot \sqrt{u^2-1}}

따라서 분자에 함수 인수의 미분을 쓰고 분모에 잠재적 함수를 다시 작성하고 인수 제곱에서 1을 뺀 함수의 제곱근을 곱합니다.

f(x)=\text{arccosec}(2x^3+9x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{6x^2+9}{(2x^3+9x)\cdot \sqrt{\left(2x^3+9x\right)^2-1}}

댓글 달기

이메일 주소는 공개되지 않습니다. 필수 필드는 *로 표시됩니다

Scroll to Top