▷ 아크탄젠트의 미분(수식 및 예)

이 기사에서는 함수의 아크탄젠트를 유도하는 방법을 배웁니다. 또한 이러한 유형의 도함수에 대한 예를 볼 수 있으며 아크탄젠트 도함수에 대한 연습문제를 풀어 연습할 수도 있습니다. 마지막으로, 아크탄젠트 미분 공식의 증명도 보여드리겠습니다.

아크탄젠트의 미분은 무엇입니까?

x의 아크탄젠트 미분은 1/1 더하기 x 제곱입니다.

$f(x)=\text{arctan}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1+x^2}$

따라서 함수의 아크탄젠트 도함수는 해당 함수의 도함수를 1로 나눈 값과 해당 함수의 제곱을 더한 값과 같습니다.

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

이 경우 함수는 au로 표시되므로 이것이 함수 u의 아크탄젠트 도함수 공식이 됩니다.

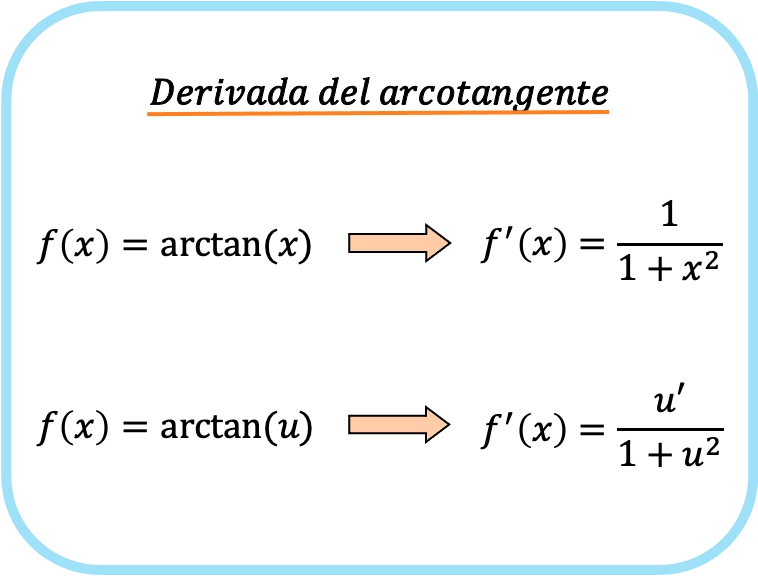
보시다시피, 역탄젠트 미분 공식은 아크사인 및 아크코사인 미분 공식과 매우 유사합니다.

아크탄젠트 도함수의 예

아크탄젠트의 도함수 공식을 알게 되면 이러한 유형의 삼각함수 도함수에 대한 몇 가지 예의 유도를 설명할 것입니다. 이렇게 하면 함수의 아크탄젠트가 어떻게 파생되는지 이해하는 것이 더 쉬울 것입니다.

예 1: 2x 아크탄젠트의 미분

$f(x)=\text{arctan}(2x)$

우리는 도함수를 풀기 위해 공식을 적용합니다:

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

2x의 도함수는 2이므로 2x의 아크탄젠트 도함수는 2/1 + 2x 제곱입니다.

$f(x)=\text{arctan}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{1+(2x)^2}}=\cfrac{2}{1+ 4x^2}$

예 2: x 제곱의 아크탄젠트 파생

$f(x)=\text{arctan}(x^2)$

이 예의 도함수 결과를 찾으려면 아크탄젠트 도함수 공식을 사용해야 합니다.

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

따라서 함수 x ² 의 도함수는 2x이므로 x의 아크탄젠트를 2제곱한 도함수는 다음과 같습니다.

$f(x)=\text{arctan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{1+\left(x^2\right)^2}=\cfrac{2x}{1+x^4}$

예 3: x 사인의 아크탄젠트 도함수

$f(x)=\text{arctan}\bigl(\text{sen}(x)\bigr)$

논리적으로 도함수를 계산하려면 해당 공식을 적용해야 합니다.

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

이 경우에는 복합 함수가 있으므로 아크탄젠트의 도함수를 계산하려면 체인 규칙을 적용해야 합니다.

$f(x)=\text{arctan}\bigl(\text{sen}(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{\text{cos}(x)}{1+\text{sen}^2(x)}$

아크탄젠트 미분에 대한 연습문제 해결

다음 아크탄젠트 함수를 도출합니다.

$\text{A) } f(x)=\text{arctan}(x^3)$

$\text{B) } f(x)=\cfrac{\text{arctan}(3x^4)}{2}$

$\text{C) } f(x)=\text{arctan}(x^5-3x^3+10)$

$\text{D) }f(x)=\text{arctan}^3(4x^2)$

$\text{E) }f(x)=\text{arctan}\bigl(\ln(x)\bigr)$

$\text{F) } f(x)=\text{arctan}\left(\sqrt{x^2+2x}\right)$

솔루션 보기

$\text{A) } f'(x)=\cfrac{3x^2}{1+\left(x^3\right)^2}=\cfrac{3x^2}{1+x^6}$

$\text{B) } f'(x)=\cfrac{12x^3}{2\left(1+\left(3x^4\right)^2\right)}=\cfrac{6x^3}{1+9x^8}$

$\text{C) } f'(x)=\cfrac{5x^4-9x^2}{1+\left(x^5-3x^3+10\right)^2}$

$\text{D) } f'(x)=3\text{arctan}^2(4x^2)\cdot \cfrac{8x}{1+\left(4x^2\right)^2}=\cfrac{24x\cdot\text{arctan}^2(4x^2)}{1+16x^2}$

$\text{E) } f'(x)=\cfrac{\cfrac{1}{x}}{1+\bigl(\ln(x)\bigr)^2}=\cfrac{1}{x\left(1+\ln^2(x)\right)}$

$\text{F) } f'(x)=\cfrac{1}{1+\left(\sqrt{x^2+2x}\right)^2}\cdot \cfrac{2x+2}{2\sqrt{x^2+2x}}=\cfrac{x+1}{\left(1+x^2+2x\right)\sqrt{x^2+2x}}$

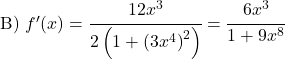
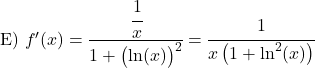
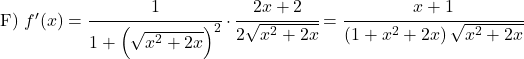
아크탄젠트의 미분 공식 시연

다음으로 아크탄젠트의 미분 공식을 증명하겠습니다.

$y=\text{arctan}(x)$

먼저 아크탄젠트가 탄젠트의 역함수라는 사실을 이용하여 아크탄젠트를 탄젠트로 변환합니다.

$x=\text{tan}(y)$

우리는 방정식의 양면을 구별합니다:

$1=\cfrac{1}{\text{cos}^2(y)}\cdot y'$

우리는 지우고 ‘:

$y'=\text{cos}^2(y)$

반면, 기본적인 삼각법 항등식 덕분에 사인과 코사인의 제곱의 합은 1이라는 것을 알 수 있습니다. 따라서 이전 표현식을 분수로 변환할 수 있습니다.

$\text{sen}^2(y)+\text{cos}^2(y)=1$

$y'=\cfrac{\text{cos}^2(y)}{1}=\cfrac{\text{cos}^2(y)}{\text{sen}^2(y)+\text{cos}^2(y)}$

모든 항을 코사인의 제곱으로 나눕니다.

$y'=\cfrac{\cfrac{\text{cos}^2(y)}{\text{cos}^2(y)}}{\cfrac{\text{sen}^2(y)}{\text{cos}^2(y)}+\cfrac{\text{cos}^2(y)}{\text{cos}^2(y)}}$

$y'=\cfrac{1}{\cfrac{\text{sen}^2(y)}{\text{cos}^2(y)}+1}$

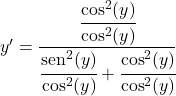
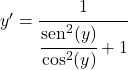
사인을 코사인으로 나눈 값은 탄젠트와 동일하므로 다음과 같습니다.

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

$y'=\cfrac{1}{\text{tan}^2(y)+1}$

위에서 본 것처럼 탄젠트는 변수 x와 동일하므로 아크탄젠트 도함수 공식에 도달하기 위해 표현식을 대체할 수 있습니다.

$y'=\cfrac{1}{x^2+1}$

아크탄젠트의 미분은 무엇입니까?

아크탄젠트 도함수의 예

예 1: 2x 아크탄젠트의 미분

예 2: x 제곱의 아크탄젠트 파생

예 3: x 사인의 아크탄젠트 도함수

아크탄젠트 미분에 대한 연습문제 해결

아크탄젠트의 미분 공식 시연

댓글 달기 댓글 취소