쌍곡선 탄젠트 함수

이 페이지에서는 쌍곡선 탄젠트에 관한 모든 것을 찾을 수 있습니다: 공식, 그래픽 표현, 모든 특성 등은 무엇입니까?

쌍곡탄젠트 공식

쌍곡선 탄젠트 함수는 주요 쌍곡선 함수 중 하나이며 기호 tanh(x) 로 표시됩니다. 수학적으로 쌍곡선 탄젠트는 쌍곡선 사인을 쌍곡선 코사인으로 나눈 값과 같습니다.

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

쌍곡선 사인 공식 과 쌍곡선 코사인 공식 으로부터 다음 표현식에 도달할 수 있습니다.

$\text{tanh}(x)=\cfrac{e^x-e^{-x}}{e^x+e^{-x}}$

따라서 쌍곡선 탄젠트 함수는 지수 함수와 관련이 있습니다. 다음 링크에서 이러한 유형의 함수의 모든 특성을 볼 수 있습니다.

➤ 참조: 지수 함수의 특성

쌍곡선 탄젠트의 그래픽 표현

공식을 통해 쌍곡선 탄젠트 함수를 그래픽으로 표현할 수 있습니다.

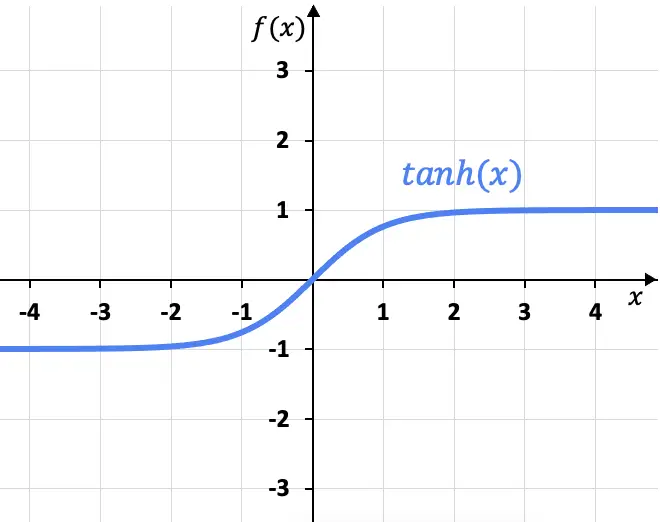
그래프에서 볼 수 있듯이, 쌍곡선 탄젠트 함수는 x=+1과 x=-1에서 두 개의 수평 점근선을 가집니다. 왜냐하면 x가 플러스 무한대에 접근할 때 함수의 극한은 x=+1을 제공하고 마이너스 무한대에 대한 극한은 x=+1을 제공하기 때문입니다. x=-1을 제공합니다.

반면, 쌍곡선 탄젠트 그래프는 주기함수인 탄젠트(삼각함수) 그래프와는 아무런 관련이 없습니다. 다음 링크에서 탄젠트의 그래픽 표현과 쌍곡선 탄젠트와의 차이점을 확인할 수 있습니다.

➤ 참조: 접선 함수의 그래픽 표현

쌍곡탄젠트의 특성

쌍곡선 탄젠트 함수에는 다음과 같은 속성이 있습니다.

쌍곡선 탄젠트 함수의 정의역은 모두 실수입니다.

$\text{Dom } f = \mathbb{R}$

반면 쌍곡선 탄젠트 함수의 경로나 범위는 -1과 +1(포함되지 않음) 사이의 값으로 제한됩니다.

$\text{Im } f= (-1,1)$

쌍곡선 탄젠트는 연속적이고 전단사적이며 홀수 함수(좌표 원점에 대해 대칭)입니다.

$\displaystyle \text{tanh}(-x) =- \text{tanh}(x)$

이 함수는 좌표 원점에서 X축과 Y축을 교차합니다.

$(0,0)$

쌍곡선 탄젠트 함수의 플러스/마이너스 무한대 한계는 +1/-1을 제공합니다. 따라서 함수는 x=+1에서 수평 점근선을 갖고 x=-1에서 또 다른 수평 점근선을 갖습니다.

$\displaystyle\lim_{x\to+\infty}\text{tanh}(x)=+1$

$\displaystyle\lim_{x\to-\infty}\text{tanh}(x)=-1$

쌍곡선 탄젠트는 전체 영역에 걸쳐 엄격하게 증가하므로 상대 극값(최대값도 최소값도 아님)이 없습니다.

그러나 함수는 x = 0 지점에서 볼록형에서 오목형으로 변경되므로 x = 0이 함수의 변곡점입니다.

쌍곡선 탄젠트 함수의 역함수를 쌍곡선 탄젠트(또는 쌍곡선 아크탄젠트) 인수라고 하며 그 공식은 다음과 같습니다.

$\displaystyle\text{tanh}^{-1}(x)=\text{arg tanh}(x)=\cfrac{1}{2}\ln\left(\frac{1+x}{1-x}\right)$

쌍곡선 탄젠트 함수의 도함수는 1을 쌍곡선 코사인의 제곱으로 나눈 값입니다.

$f(x)=\text{tanh}(x) \ \longrightarrow \ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=1-\text{tanh}^2(x)$

쌍곡선 탄젠트 함수의 적분은 쌍곡선 코사인의 자연 로그입니다.

$\displaystyle\int\text{tanh}(x) \ dx= \ln\Bigl(\text{cosh}(x)\Bigr)+C$

서로 다른 두 숫자의 합에 대한 쌍곡선 탄젠트는 다음 방정식을 적용하여 계산할 수 있습니다.

$\text{tanh}(x+y)=\cfrac{\text{tanh}(x)+\text{tanh}(y)}{1+\text{tanh}(x)\cdot \text{tanh}(y)}$

Taylor 다항식 또는 쌍곡선 탄젠트 계열은 수렴 반경을 갖습니다.
$\left|x\right|<\cfrac{\pi}{2}$

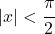
다음 표현식에 해당합니다.

$\displaystyle\text{tanh}(x)=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\cdots =\sum_{n=1}^\infty\frac{2^{2n}(2^{2n}-1)B_{2n} x^{2n-1}}{(2n)!}$

금

$B_n$

베르누이 수 입니다.

쌍곡탄젠트 공식

쌍곡선 탄젠트의 그래픽 표현

쌍곡탄젠트의 특성

댓글 달기 댓글 취소