쌍곡코시컨트의 도함수 - 마토리티(Mathority)

이 글에서는 함수의 쌍곡코시컨트를 유도하는 방법을 설명합니다. 추가적으로, 쌍곡코시컨트의 도함수에 대한 몇 가지 해결된 예를 볼 수 있습니다.

쌍곡코시컨트의 도함수에 대한 공식

x의 쌍곡 코시컨트의 도함수는 x의 쌍곡 코시컨트 곱하기 x의 쌍곡 코시컨트를 빼는 것과 같습니다.

$f(x)=\text{cosech}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(x)\cdot \text{cotgh}(x)$

그러므로, 함수의 쌍곡 코시컨트의 도함수는 함수의 쌍곡 코시컨트 곱하기 함수의 쌍곡 코시컨트 곱하기 상기 함수의 도함수를 뺀 값입니다.

$f(x)=\text{cosech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(u)\cdot \text{cotgh}(u)\cdot u'$

간단히 말해서, 함수의 코시컨트를 유도하는 공식은 다음과 같습니다.

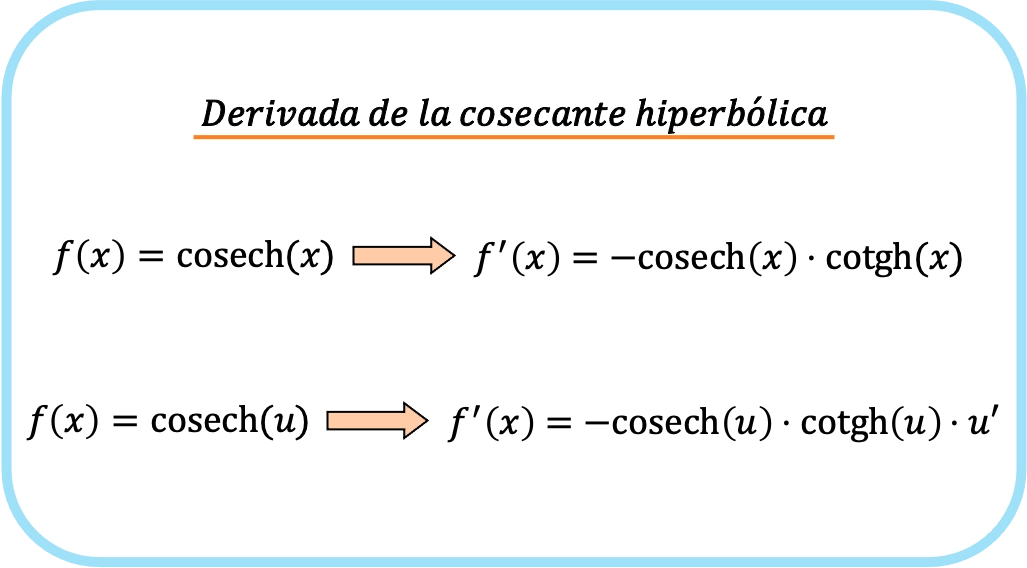
실제로 앞의 두 수식은 하나의 수식에 해당하는데, 차이점은 두 번째 수식에 연쇄법칙이 적용된다는 점이다.

쌍곡 코시컨트의 도함수에 대한 공식이 무엇인지 확인한 후, 여기에 이러한 유형의 삼각 도함수에 대한 몇 가지 작업된 예가 있습니다.

이 첫 번째 예에서는 x 제곱의 쌍곡선 코시컨트를 유도합니다.

$f(x)=\text{cosech}(x^2)$

쌍곡코시컨트 인수의 함수는 x와 다르므로, 연쇄 법칙을 사용하여 쌍곡코시컨트의 도함수에 대한 공식을 사용해야 합니다.

$f(x)=\text{cosech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(u)\cdot \text{cotgh}(u)\cdot u'$

따라서 이 삼각 함수를 도출하려면 이전 공식의 값, 즉 쌍곡 코시컨트와 쌍곡 탄젠트의 인수에 x ^{2 를} 대입하고 모든 값에 도함수를 곱하면 됩니다. x의 제곱은 2x입니다.

$f(x)=\text{cosech}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(x^2)\cdot \text{cotgh}(x^2)\cdot 2x$

이 연습에서는 x의 쌍곡선 코시컨트의 도함수를 세제곱한 값이 얼마나 되는지 살펴보겠습니다.

$f(x)=\text{cosech}(x^3)$

함수의 쌍곡코시컨트의 도함수를 찾기 위해 다음 공식을 적용합니다.

$f(x)=\text{cosech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(u)\cdot \text{cotgh}(u)\cdot u'$

x 세제곱의 도함수는 3x ² 이므로 전체 함수의 도함수는 다음과 같습니다.

$f(x)=\text{cosech}(x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{cosech}(x^3)\cdot \text{cotgh}(x^3)\cdot 3x^2$