쌍곡선 시컨트 도함수

이 글에서는 함수의 쌍곡선 시컨트를 유도하는 방법을 설명합니다. 쌍곡선 시컨트의 도함수에 대한 공식과 이러한 유형의 도함수에 대한 몇 가지 작업 예제를 찾을 수 있습니다.

쌍곡선 시컨트의 도함수에 대한 공식

x의 쌍곡선 시컨트의 도함수는 x의 쌍곡선 탄젠트 곱하기 x의 쌍곡선 시컨트 곱을 뺀 것과 같습니다.

$f(x)=\text{sech}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(x)\cdot \text{tanh}(x)$

그러므로, 함수의 쌍곡선 시컨트의 도함수는 함수의 쌍곡선 시컨트 곱하기 함수의 쌍곡선 탄젠트 곱하기 상기 함수의 도함수의 곱을 뺀 것입니다.

$f(x)=\text{sech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(u)\cdot \text{tanh}(u)\cdot u'$

즉, 쌍곡선 시컨트 함수의 미분 공식은 다음과 같습니다.

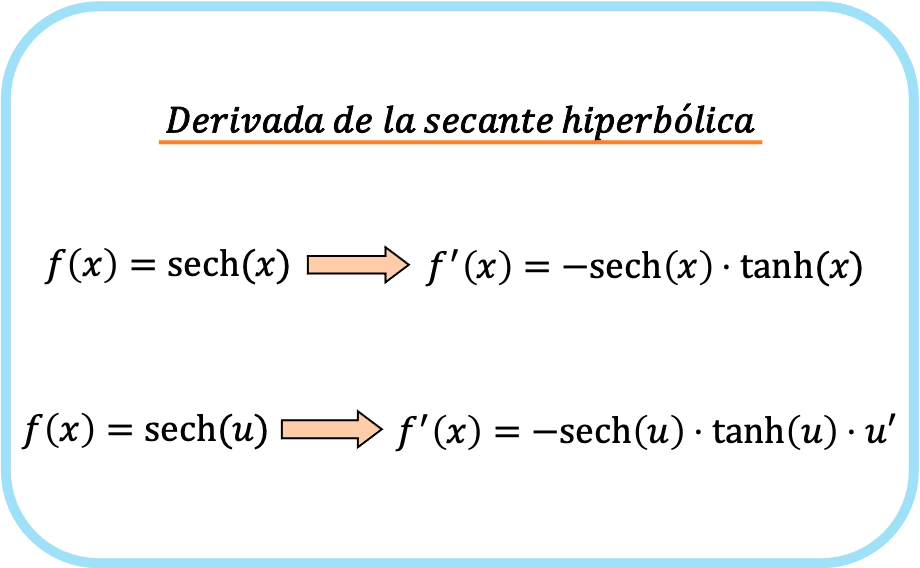
두 표현식 모두 실제로는 단일 수식에 속합니다. 유일한 차이점은 두 번째 공식에서는 체인 규칙이 적용된다는 것입니다.

이제 우리는 쌍곡선 시컨트의 미분에 대한 공식을 알았으므로 이러한 유형의 삼각 미분에 대한 몇 가지 해결된 연습을 볼 것입니다.

$f(x)=\text{sech}(2x)$

이 예에서는 쌍곡선 시컨트 인수의 x와 다른 함수가 있으므로 이를 파생하려면 체인 규칙 공식을 사용해야 합니다.

$f(x)=\text{sech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(u)\cdot \text{tanh}(u)\cdot u'$

함수 2x는 선형이므로 그 도함수는 2입니다. 따라서 도함수를 찾으려면 공식에서 u를 2x로 바꾸고 u’를 2로 바꾸면 됩니다.

$f(x)=\text{sech}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(2x)\cdot \text{tanh}(2x)\cdot 2$

$f(x)=\text{sech}(x^2)$

이 연습의 기능은 복합적입니다. 왜냐하면 쌍곡선 시컨트는 인수에서 또 다른 기능을 갖고 있기 때문입니다. 그러므로 우리는 이를 도출하기 위해 체인 규칙과 함께 쌍곡선 시컨트 공식을 사용해야 합니다:

$f(x)=\text{sech}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(u)\cdot \text{tanh}(u)\cdot u'$

x를 2로 올리면 도함수는 2x가 됩니다. 따라서 x 제곱의 쌍곡선 시컨트 도함수는 다음과 같습니다.

$f(x)=\text{sech}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\text{sech}(x^2)\cdot \text{tanh}(x^2)\cdot 2x$