이 글에서는 함수의 쌍곡선코시컨트를 유도하는 방법을 설명합니다. 또한 쌍곡선 역코시컨트의 도함수에 대한 작업된 예도 찾을 수 있습니다.
쌍곡선 코시컨트 호의 도함수에 대한 공식
x의 아크 쌍곡선 코시컨트의 도함수는 -1을 x 곱하기 1의 루트 + x 제곱의 곱으로 나눈 값과 같습니다.
![]()
그러므로, 함수의 아크쌍곡선 코시컨트의 도함수는 상기 함수의 도함수를 함수 곱하기 1의 근에 제곱 함수를 더한 곱으로 나눈 값입니다.
![]()
요약하면, 쌍곡선 아크코시컨트 함수의 도함수를 계산하는 공식은 다음과 같습니다.
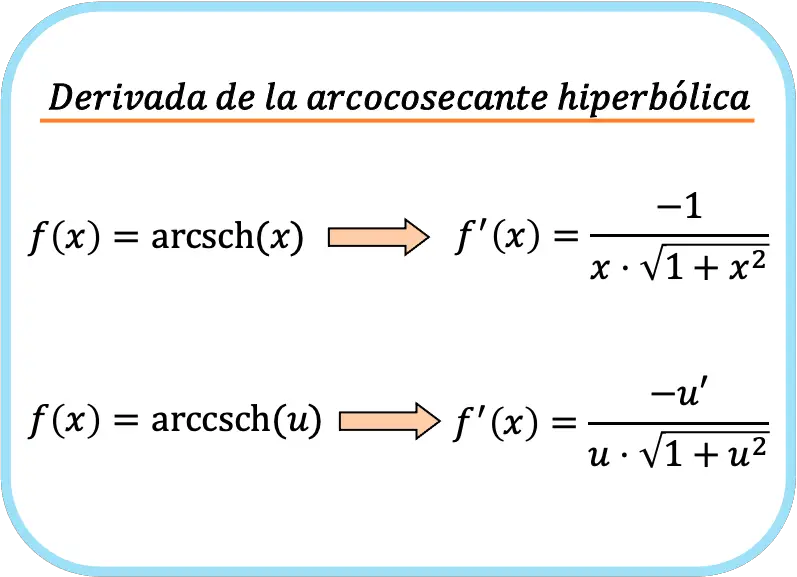
두 가지 공식을 넣었다고 해서 그것이 다르다는 의미는 아닙니다. 자세히 살펴보면 두 번째 공식은 첫 번째 공식과 같지만 체인 규칙을 적용한 것입니다.
쌍곡선 코시컨트 호의 도함수 예
쌍곡선 코시컨트의 도함수에 대한 공식이 주어지면 우리는 그러한 함수 두 개를 유도하여 이것이 어떻게 수행되는지 볼 수 있습니다.
실시예 1
![]()
이 연습에서는 인수에 x와 다른 함수가 있기 때문에 체인 규칙을 사용하여 아크 쌍곡선 코시컨트의 도함수 공식을 사용해야 합니다.
![]()
따라서 도함수를 찾으려면 u를 3x로 바꾸고 u’를 해당 도함수인 3으로 바꿔야 합니다.
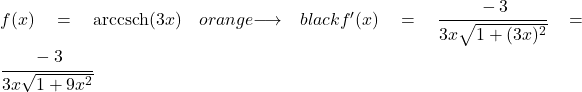
실시예 2
![]()
이 경우 쌍곡선 역코시컨트 인수에 다항식 함수가 있으므로 이를 파생하기 위해 체인 규칙도 사용해야 합니다.
![]()
따라서 우리는 분수의 분자에 인수 함수의 도함수를 넣고 분모에서는 다항식 함수에 의해 u를 변경합니다.
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arccsch}(x^5-2x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(5x^4-6x^2)}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\\[1.5ex] &=\cfrac{-5x^4+6x^2}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6257584425bd348ba75c7680d8ff6f70_l3.png)
유사한 항목
- 쌍곡선 아크코사인의 파생물
- 쌍곡코시컨트의 도함수
- 쌍곡선 코사인의 미분
- 코시컨트 호의 미분
- 코시컨트에서 파생
- 아크코사인의 미분
- 코사인의 파생물