쌍곡사인 함수

7월 4, 2023

이 기사에서는 쌍곡사인에 관한 모든 것을 찾을 수 있습니다: 공식, 그래픽 표현, 모든 특성, 다른 함수와의 관계 등은 무엇입니까?

쌍곡사인 공식

쌍곡선 사인 함수는 주요 쌍곡선 함수 중 하나이며 기호 sinh(x) 또는 sinh(x) 로 표시됩니다. 쌍곡사인은 e ^x 빼기 e ^-x를 2로 나눈 값과 같습니다.

따라서 쌍곡사인의 공식은 다음과 같습니다.

$\displaystyle\text{senh}(x)=\cfrac{e^{x}-e^{-x}}{2}$

따라서 쌍곡선 사인은 지수 함수와 관련이 있습니다.

➤ 참조: 지수 함수의 특성

쌍곡선 사인의 그래픽 표현

이전 섹션에서 본 공식을 사용하여 쌍곡사인 값 테이블을 만들고 함수 그래프를 작성할 수 있습니다.

쌍곡사인

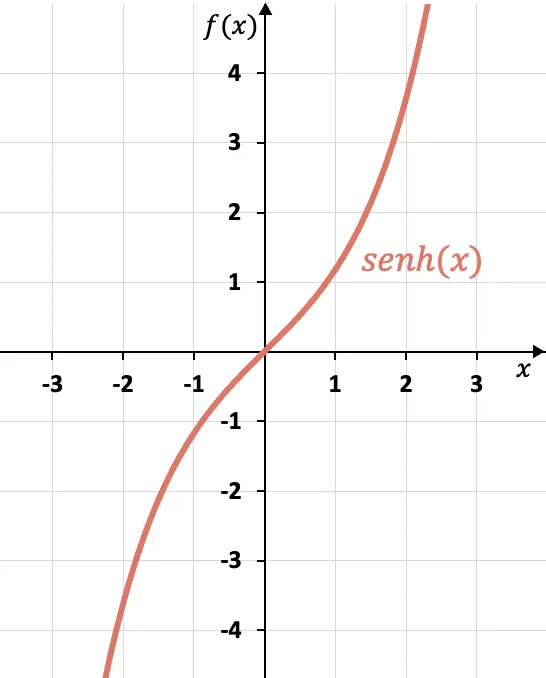
이 그래프에서 우리는 쌍곡선 사인이 홀수 함수라는 것을 알 수 있습니다. 왜냐하면 반대편 x는 반대 이미지를 갖기 때문입니다. 즉, 쌍곡선 사인 그래프는 좌표 원점(0, 0)을 기준으로 대칭입니다.

보시다시피, 쌍곡선 사인 그래프는 주기 함수인 사인 그래프와 매우 다릅니다. 다음 링크에서 사인의 그래픽 표현과 쌍곡선 사인과의 모든 차이점을 볼 수 있습니다.

➤ 참조: 사인 함수의 그래픽 표현

쌍곡사인의 특성

쌍곡선 사인에는 다음과 같은 속성이 있습니다.

쌍곡사인 함수의 정의역은 모두 실수입니다.

$\text{Dom } f = \mathbb{R}$

쌍곡선 사인 함수의 범위 또는 범위도 모두 실수입니다.

$\text{Im } f= \mathbb{R}$

쌍곡사인은 연속적이고 홀수 함수입니다.

$\displaystyle \text{senh}(-x) =- \text{senh}(x)$

동일한 교차점, 좌표 원점에서 X축과 Y축을 차단합니다.

$(0,0)$

x가 플러스/마이너스 무한대에 가까워질 때 쌍곡사인 함수의 한계는 플러스/마이너스 무한대와 같습니다.

$\displaystyle\lim_{x\to+\infty}\text{senh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{senh}(x)=-\infty$

쌍곡사인은 영역 전체에서 엄격하게 증가하므로 최대값이나 최소값이 없습니다.

그러나 x = 0 지점에서 곡률이 변경되므로 이는 함수의 변곡점입니다. x=0보다 작은 값에 대해서는 오목 함수이고, 반면에 x=0보다 큰 값에 대해서는 볼록 함수입니다.

쌍곡선 사인 함수의 파생물은 쌍곡선 코사인입니다.

$f(x)=\text{senh}(x) \ \longrightarrow \ f'(x)=\text{cosh}(x)$

마찬가지로 쌍곡선 사인 함수의 적분은 쌍곡선 코사인입니다.

$\displaystyle \int \text{senh}(x) \ dx= \text{cosh}(x) + C$

쌍곡사인 함수의 테일러 급수는 다음 표현식과 동일합니다.

$\displaystyle\text{senh}(x)=x+\cfrac{x^3}{3!}+\cfrac{x^5}{5!}+\cfrac{x^7}{7!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n+1}}{(2n+1)!}$

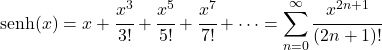
쌍곡사인 함수의 라플라스 변환은 다음과 같습니다.

$\mathcal{L}\bigl[\text{senh}(at)\bigr]=\cfrac{a}{s^2-a^2}$

쌍곡사인의 수학적 관계

쌍곡선 사인은 다음 방정식을 통해 다른 쌍곡선 함수에 연결됩니다.

기본 방정식은 쌍곡선 사인을 쌍곡선 코사인과 연관시킵니다.

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

따라서 쌍곡선 사인 및 코사인 함수는 x ² -y ² =1인 쌍곡선 방정식으로 관련됩니다. 원 방정식(x ² +y ² =1)으로 연결된 삼각 사인 및 코사인 함수와는 다릅니다.

사인, 코사인 및 탄젠트의 쌍곡선 함수는 다음 방정식으로 연관될 수 있습니다.

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

반면, 서로 다른 두 숫자의 덧셈이나 뺄셈에 대한 쌍곡사인은 다음 공식을 사용하여 계산할 수 있습니다.

$\text{senh}(x+y)=\text{senh}(x)\text{cosh}(y)+\text{senh}(y)\text{cosh}(x)$

$\text{senh}(x-y)=\text{senh}(x)\text{cosh}(y)-\text{senh}(y)\text{cosh}(x)$

숫자 두 배의 쌍곡사인은 다음 수학적 관계를 적용하여 결정할 수 있습니다.

$\text{senh}(2x)=2\text{senh}(x)\text{cosh}(x)$

두 쌍곡사인의 합이나 빼기는 다음 공식을 사용하여 구할 수 있습니다.

$\displaystyle\text{senh}(x)+\text{senh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{senh}(x)-\text{senh}(y)=2\text{senh}\left(\frac{x-y}{2}\right)\text{cosh}\left(\frac{x+y}{2}\right)$

마지막으로 쌍곡사인의 제곱은 다음 공식을 적용하여 계산할 수 있습니다.

$\text{senh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)-1\Bigr)$

댓글 달기 댓글 취소