여기에서 항등 함수가 무엇인지 확인할 수 있습니다. 또한 항등함수를 그래픽적으로 어떻게 표현하는지, 그 특징은 무엇인지 알아볼 수 있을 것이다.
신원 기능이란 무엇입니까?
항등 함수는 인수와 동일한 값을 이미지로 갖는 함수입니다. 항등함수는 id라는 용어로 표현될 수 있습니다.
따라서 항등 함수의 수학적 표현은 다음과 같습니다.
![]()
예를 들어, x=1에 대한 항등함수 이미지는 1의 가치가 있고, x=2의 이미지는 2의 가치가 있으며, x=3의 이미지는 3의 가치가 있습니다.
![Rendered by QuickLaTeX.com \begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b85e48e3f36d1eb4271b265aaf35bef_l3.png)
항등 함수는 선형 함수의 예입니다. 다음 링크에서 이러한 유형의 함수에 대한 더 많은 예를 볼 수 있습니다.
➤ 참조: 선형 함수의 예
항등 함수의 그래픽 표현
항등함수의 그래프는 제1사분면과 제3사분면의 이등분선에 해당합니다.
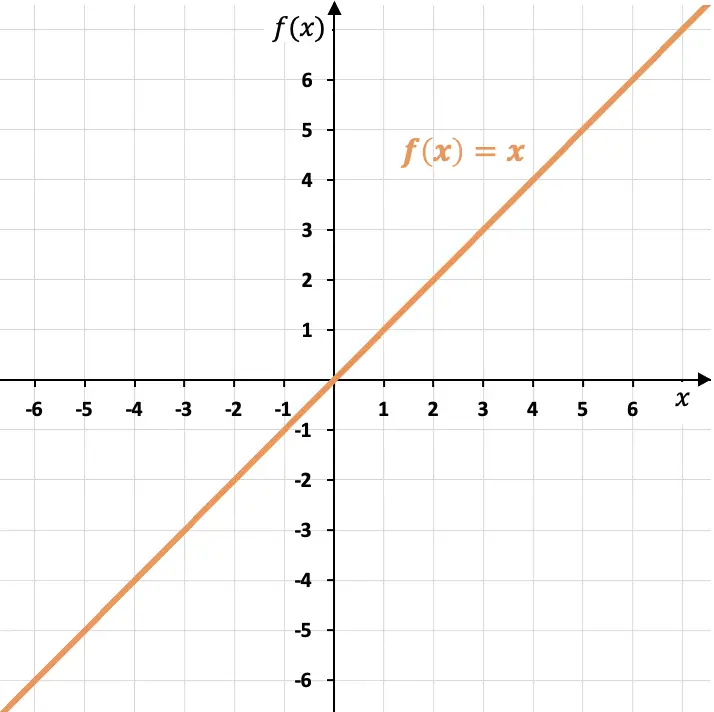
보시다시피, 항등 함수는 좌표의 원점(점(0,0))을 통과하고 단일(m=1)과 동일한 기울기를 갖습니다. 왜냐하면 변수의 한 단위가 증가하고 각 독립 값에 대해 증가하기 때문입니다. 변수 X. 또한 항등 함수는 X축과 45°의 각도를 형성합니다.
항등함수의 특징
항등 함수에는 다음과 같은 속성이 있습니다.
- 항등 함수의 정의역은 모두 실수입니다.
![]()
- 항등 함수의 범위(또는 범위)도 모두 실수로 구성됩니다.
![]()
- 항등함수는 연속적이고 전단사적인 함수입니다.
- 또한 항등함수는 홀수함수로 구성되는데, 이는 좌표원점을 기준으로 대칭함수임을 의미한다.
![]()
➤ 참조: 홀수 대칭 함수
- 항등함수는 전체 영역에 걸쳐 증가하며 기울기는 1입니다.
![]()
- x축(OX축)과 y축(Y축)이 같은 점, 즉 좌표 원점에서 교차합니다.
![]()
- 1차 다항식 함수로 분류할 수 있습니다.
- 항등함수는 함수 합성 의 중립 요소로 작용합니다. 따라서 항등 함수로 구성된 모든 함수는 함수 자체가 됩니다.
![]()
- 가치
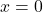
이 유형의 함수의 유일한 루트입니다.
- x가 플러스 무한대 또는 마이너스 무한대를 향할 때 항등 함수의 극한은 각각 플러스 무한대와 마이너스 무한대를 제공합니다.
![]()
![]()
- 따라서 항등 함수에는 점근선이 없습니다.
- 항등 함수의 미분은 값이 1인 상수 함수입니다.
![]()
- 항등 함수의 적분은 이차 함수입니다.
![]()
➤ 참조: 이차 함수 공식