▷ 숫자의 계승: 그것이 무엇인지, 어떻게 계산하는지 ✅

이 페이지에서는 숫자의 계승이 무엇인지, 그리고 계산 방법을 설명합니다. 또한, 몇 가지 예와 가장 많이 사용되는 계승 값이 포함된 표가 제시되어 있습니다. 또한 계산기를 사용하여 숫자의 계승을 계산하는 방법도 가르칩니다. 그리고 마지막으로 팩토리얼의 응용과 특성을 설명합니다.

숫자의 계승이란 무엇입니까?

수학에서 숫자의 계승은 1부터 해당 숫자까지의 모든 양의 정수의 곱과 같습니다. 또한 숫자의 계승은 숫자 뒤에 느낌표(!)로 표시됩니다.

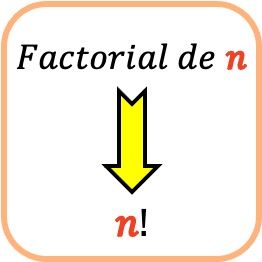
예를 들어, 계승 n 이라고도 하는 숫자 n 의 계승을 결정하려면 숫자 n 에 그 앞에 오는 모든 정수(1부터 시작)를 곱해야 합니다.

$n! = 1 \cdot 2 \cdot 3 \cdots (n-2) \cdot (n-1) \cdot n$

숫자의 계승을 계산하는 방법

숫자의 계승의 의미를 확인한 후에는 계승을 결정하는 방법을 예를 통해 살펴보겠습니다.

4의 계승을 계산합니다.

수학적 정의에서 보았듯이 숫자의 계승은 그보다 작거나 같은 모든 양의 정수를 곱하는 것과 같습니다. 따라서 4의 계승을 계산하려면 숫자 1, 2, 3, 4를 곱해야 합니다.

$4! = 1 \cdot 2 \cdot 3 \cdot 4 =24$

따라서 4의 계승은 24를 제공합니다.

숫자의 계승의 예

숫자의 계승 개념에 대한 이해를 마무리하기 위해 서로 다른 숫자의 여러 계승을 계산하는 예를 보여드리겠습니다.

3의 계승:

$3! = 1 \cdot 2 \cdot 3 =6$

5의 계승:

$5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5=120$

6의 계승:

$6! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6=720$

1의 계승:

$1! = 1$

논리적으로 숫자 1의 계승은 1을 곱하면 충분하므로 1과 같습니다.

0의 계승:

$0! = 1$

예, 알겠습니다. 놀랍게도 0의 계승은 0이 아니라 1입니다. 이론상으로는 0에 1을 곱해야 하기 때문에 이것이 조금 이상하게 보일 수 있습니다. 그러나 관례에서는 0! =1 제품 속성이 비어 있기 때문입니다. 더 알고 싶은 경우를 대비해 이 링크를 남깁니다. 이유를 아는 것이 실제로 관련성은 없지만 중요한 것은 0의 계승이 1과 같다는 것을 기억하는 것입니다.

숫자의 계승에 대한 결과 목록

아래에는 가장 많이 사용되는 숫자의 계승값이 표에 요약되어 있으므로 직접 계산할 필요가 없습니다.

수	숫자의 계승
0	1
1	1
2	2
삼	6
4	24
5	120
6	720
7	5,040
8	40,320
9	362,880
십	3,628,800
열하나	39,916,800
12	479,001,600
13	6,227,020,800
14	87 178 291 200
열 다섯	1,307,674,368,000
16	20,922,789,888,000
17	355,687,428,096,000
18	6,402,373,705,728,000
19	121,645,100,408,832,000
이십	2,432,902,008 176,640,000
오십	3,041,409,320 · ^10.64
100	9,332 621,544 · ^10,157
1,000	4,023,872,601 · ^10.2567
10,000	2,846,259,681 · ^10,35,659
100,000	2 824 229 408 · 10 ^{45 6573}
1,000,000	8,263,931,688 · 10 ^5,565,708

계산기를 사용한 숫자의 계승

이전 예에서 볼 수 있듯이 연속된 두 숫자의 계승 결과는 기하급수적으로 증가하므로 큰 숫자의 계승을 아는 것이 상당히 어렵습니다. 그래서 우리는 계산기를 사용하여 숫자의 계승을 찾는 방법을 보여 드리겠습니다.

공학용 계산기에는 x 기호가 있는 키가 있습니다! 아니면 엔! 이는 정수의 계승을 계산하는 데 사용됩니다. 따라서 팩토리얼의 가치를 결정하려면 계산기에서 다음 순서를 수행해야 합니다.

$n! \quad \color{red} \bm{\longrightarrow} \quad \color{black} n\rightarrow \boxed{x!} \rightarrow \boxed{=}$

일반적으로 CASIO 계산기에는 계승 키 x!가 있습니다. 아니면 엔! x ^-1 버튼 위에 있습니다.

예를 들어, 계산기를 사용하여 계승 문제를 풀어서 어떻게 계산하는지 알고 있는지 확인할 것입니다. 예를 들어, 9의 계승을 수행하겠습니다.

$9! \quad \color{red} \bm{\longrightarrow} \quad \color{black} 9\rightarrow \boxed{x!} \rightarrow \boxed{=} \rightarrow 362880$

9의 계승을 찾으려면 먼저 숫자 9를 입력한 다음 키를 눌러야 합니다.

$\boxed{x!}$

마지막으로 등호 버튼을 누르세요. 이 경우 계산기에는 362,880이라는 결과가 표시됩니다.

팩토리얼 번호의 적용

숫자의 계승 함수는 매우 간단하고 터무니없는 연산처럼 보일 수 있지만 고급 대수학에서는 꽤 많이 사용됩니다. 그런 다음 계승의 주요 용도를 살펴보겠습니다.

우선, 팩토리얼은 특정 연산 이상의 조합수를 계산하기 위한 필수 연산이다. 조합수가 무엇인지 모른다면, 이 링크에서 조합수가 무엇으로 구성되어 있는지, 어떻게 계산되는지 확인할 수 있습니다. 여기서 예, 해결된 연습문제 및 그 속성이 무엇인지 확인할 수 있습니다. 또한 실제 응용 프로그램이 많기 때문에 어떤 용도로 사용되는지 확인할 수 있습니다.

계승은 함수의 테일러 다항식을 결정하기 위해 수학에서도 사용됩니다.

마찬가지로 계승은 특정 조합 문제를 해결하는 데, 특히 조합과 순열을 계산하는 데 사용됩니다. 이러한 의미에서 계승은 조합론을 사용하여 확률을 계산하는 데에도 자주 사용됩니다.

n개 요소의 순열은 이러한 요소로 만들 수 있는 서로 다른 배열 각각에 해당합니다. 따라서 순열을 계산하려면 계승이 사용됩니다. 예를 들어, 어떤 문제에서 7개의 물체를 배열할 수 있는 가능성의 수를 구하려면 7의 계승을 계산해야 합니다.

이제 해결된 연습 문제를 살펴보겠습니다.

신발이 5켤레 있는데 어떻게 정리할 수 있나요?

이 연습에서 우리는 신발을 넣은 순서를 고려하여 5켤레의 신발을 결합할 수 있는 가능한 모든 방법을 찾아야 합니다. 따라서 문제를 해결하려면 5의 계승값을 계산하면 됩니다.

$5! = 1\cdot 2 \cdot 3\cdot 4\cdot 5 =120$

즉, 5켤레의 신발을 120가지 방법으로 배치할 수 있다는 것입니다.

팩토리얼 넘버의 속성

팩토리얼 번호에는 다음과 같은 특징이 있습니다.

n이 m보다 큰 두 개의 양의 정수 n 과 m 이면 분명히 n 의 계승 값은 m 의 계승 값보다 큽니다.

$n>m \quad \longrightarrow \quad n! > m!” title=”Rendered by QuickLaTeX.com” height=”15″ width=”183″ style=”vertical-align: -2px;”> <ul style=$

숫자의 계승은 요인 중 하나가 더 작은 숫자의 계승이 되도록 계승 분해될 수 있습니다.

$n>m \quad \longrightarrow \quad n!= n\cdot (n-1) \cdots (m+1)\cdot m!” title=”Rendered by QuickLaTeX.com” height=”19″ width=”361″ style=”vertical-align: -5px;”> 예를 들어, 6은 4보다 크므로 6의 계승에 대한 표현식은 다음과 같이 단순화될 수 있습니다. <p class=$ $6! = 6 \cdot 5 \cdot 4!$

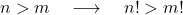
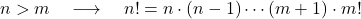
다음 대수식은 1의 계승을 제외한 모든 숫자의 계승에 유효합니다.

$\displaystyle n!< \left( \frac{n+1}{2} \right)^n$

음수 또는 소수의 계승

우리는 방금 양의 정수의 계승값을 구하는 방법을 살펴보았습니다. 그런데… 음수나 십진수의 계승값을 계산할 수 있을까요? 대답은 ‘예’입니다. 하지만 수학에 대한 고급 지식이 필요합니다.

음수와 십진수의 계승은 다음 적분으로 정의되는 오일러의 “감마 함수”라는 특수 함수를 사용하여 계산됩니다.

$\displaystyle \Gamma(z)=\int_0^\infty t^{z-1} e^{-t}\, \mathrm{d}t$

따라서 다음 방정식이 항상 참이므로 모든 유형의 계승은 감마 함수를 사용하여 풀 수 있습니다.

$n! = \Gamma(n+1)$

예를 들어 0.5의 계승값을 찾으려면 다음 값을 찾아야 합니다.

$\Gamma(1,5)$

왜냐하면:

$0,5! = \Gamma(0,5+1) =\Gamma(1,5)$

그리고 적분의 해는 0.5의 계승에 해당합니다.

분명히 감마 함수의 적분을 푸는 것은 쉽지 않으며 이 기사에서는 이를 가르치지 않을 것입니다. 왜냐하면 많은 수학적 개념을 미리 설명해야 하기 때문입니다. 하지만 우리는 음수나 십진수의 계승을 계산할 가능성이 있다는 것을 알려드리고 싶었습니다.

실제로 예를 들어 우리는 몇 가지 음의 계승값과 소수점 값을 계산했습니다.

$\underline{\bm{n}}$	$\underline{\bm{n!}}$
$\displaystyle \left(\frac{1}{2}\right)!$	$\displaystyle \frac{1}{2}\sqrt{\pi}$
$\displaystyle \left(-\frac{1}{2}\right)!$	$\displaystyle \sqrt{\pi}$
$\displaystyle \left(\frac{3}{2}\right)!$	$\displaystyle \frac{3}{4}\sqrt{\pi}$
$\displaystyle \left(\frac{5}{2}\right)!$	$\displaystyle \frac{15}{8}\sqrt{\pi}$