수평 점근선

이 기사에서 우리는 함수의 수평 점근선이 무엇인지, 그리고 어떻게 계산되는지 설명합니다. 또한 개념을 완전히 이해하기 위해 이러한 유형의 점근선에 대한 몇 가지 예를 찾을 수 있으며, 또한 수평 점근선의 해결 연습을 통해 연습할 수 있습니다.

수평 점근선이란 무엇입니까?

함수의 수평 점근선은 그래프가 교차하지 않고 무한정 접근하는 수평선입니다. 따라서 수평 점근선의 방정식은 y=k 입니다. 여기서 k 는 수평 점근선의 값입니다.

즉, x가 무한대에 접근할 때 함수의 극한이 k 와 같은 경우 k 는 수평 점근선입니다.

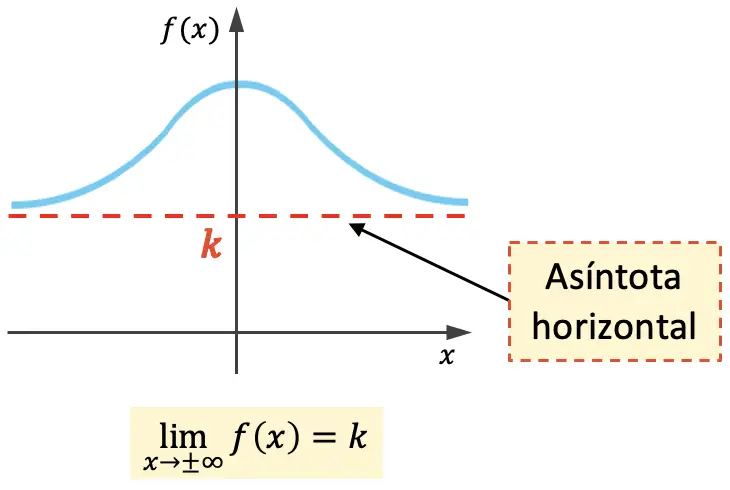
위 함수는 그래프 양쪽에 수평 점근선을 가지지만, 함수는 한쪽에만 수평 점근선을 가질 수 있습니다:

최소한 무한대까지의 극한이 실수를 제공하는 경우 함수는 왼쪽 수평 점근선을 갖습니다.
플러스 무한대에 대한 극한이 실수를 제공하는 경우 함수는 오른쪽에 수평 점근선을 갖습니다.

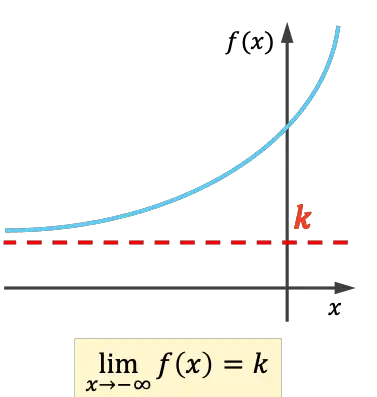
함수의 수평 점근선을 계산하는 방법

함수의 수평 점근선을 계산하려면 다음 단계를 따라야 합니다:

무한대(+무한대 및 -무한대)에 대한 함수의 극한을 계산합니다.
무한대에 대한 극한이 실수(k)를 제공하는 경우 선 y=k는 함수의 수평 점근선입니다.
어느 극한도 실수에 해당하지 않으면 함수에는 수평 점근선이 없습니다.

수평 점근선 예

따라서 이것이 어떻게 수행되는지에 대한 예를 볼 수 있습니다. 우리는 다음 유리 함수에서 모든 수평 점근선을 제거할 것입니다:

$f(x)=\cfrac{x+1}{x-1}$

수평 점근선을 결정하려면 함수의 음의 무한대와 양의 무한대에서의 극한을 계산해야 합니다.

$\displaystyle \lim_{x \to +\infty} \cfrac{x+1}{x-1} = \cfrac{+\infty}{+\infty}= \cfrac{1}{1} = \bm{1}$

$\displaystyle \lim_{x \to -\infty} \cfrac{x+1}{x-1} = \cfrac{-\infty}{-\infty}= \cfrac{1}{1} = \bm{1}$

➤ 참고: 무한 사이의 무한 불확정성을 해결하는 방법

무한대에서의 두 극한은 1을 제공하므로 y=1은 함수의 유일한 수평 점근선입니다.

아래는 그래픽으로 표현된 함수입니다. 보시다시피, 함수는 y=1(양의 무한대와 음의 무한대 모두)에 매우 가까워지지만 수평 점근선이기 때문에 절대 건드리지 않습니다.

참고: 일부 특별한 경우에 함수는 하나 이상의 점에서 수평 점근선과 교차하지만 일반적으로 함수 그래프는 점근선을 교차하지 않습니다.

반면에, 이 함수는 x=1에서 수직 점근선도 갖습니다. 그래프에서 볼 수 있듯이 x=1 선에 매우 가까워지지만 해당 값에는 도달하지 않습니다.

수평 점근선 문제 해결

연습 1

다음 분수 함수의 수평 점근선(있는 경우)을 구합니다.

$\displaystyle f(x)= \frac{4x+3}{2x-1}$

해결책 보기

유리 함수의 수평 점근선을 결정하려면 함수의 무한대에서의 극한을 계산해야 합니다.

$\displaystyle \lim_{x \to +\infty} \frac{4x+3}{2x-1} = \frac{4(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{4}{2} = \bm{2}$

$\displaystyle \lim_{x \to -\infty} \frac{4x+3}{2x-1} = \frac{4(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{4}{2} = \bm{2}$

이 경우, 불확정 형식의 결과는 분자와 분모가 동일한 차수이기 때문에 가장 높은 차수 x의 계수를 나눈 것입니다.

함수의 플러스 무한대와 마이너스 무한대에서의 극한은 2를 제공하므로 y=2는 수평 점근선이고 함수가 갖는 유일한 점근선입니다.

연습 2

근이 있는 다음 유리 함수의 수평 점근선을 모두 찾습니다.

$\displaystyle f(x)= \frac{3x}{\sqrt{x^2+2}}$

해결책 보기

함수의 수평 점근선을 찾기 위해 먼저 양의 무한대에서의 극한을 계산합니다:

$\displaystyle \lim_{x \to +\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{+\infty}{+\infty} = \frac{3}{\sqrt{1}} = \bm{3}$

그런 다음 함수의 극한을 음의 무한대로 해결합니다.

$\displaystyle \lim_{x \to -\infty}\frac{3x}{\sqrt{x^2+2}}= \frac{-\infty}{+\infty} = \frac{-3}{\sqrt{1}} = \bm{-3}$

➤ 무한대에 대한 극한이 어떻게 해결되었는지 의문이 든다면, 무한대 사이의 무한 불확정성을 해결하는 방법에 대한 위의 링크를 확인하는 것이 좋습니다.

이 경우 우리는 무한대에서 서로 다른 두 가지 극한 값을 얻었습니다. 따라서 함수에는 두 개의 수평 점근선이 있습니다. y=3은 오른쪽 함수의 수평 점근선이고, 반면에 y=-3은 왼쪽 함수의 수평 점근선입니다.

연습 3

다음 조각별로 정의된 함수의 수평 점근선을 계산합니다.

$\displaystyle f(x)=\left\{ \begin{array}{lcl}\displaystyle\frac{3x-1}{x^2}& \text{si} & x<4\\[4ex]\displaystyle\frac{x^3-2x+5}{2x^3-9} & \text{si} & x\geq 4 \end{array} \right.$

해결책 보기

함수의 수평 점근선을 계산하려면 공식은 없지만 플러스 및 마이너스 무한대에 대한 극한을 계산해야 합니다.

따라서 최소한 무한한 극한을 찾기 위해 첫 번째 섹션에서 정의한 함수를 사용합니다.

$\displaystyle \lim_{x \to -\infty}\frac{3x-1}{x^2}= \frac{-\infty}{+\infty}=\bm{0}$

따라서 선 y=0은 함수 왼쪽의 수평 점근선입니다.

이제 두 번째 섹션에 정의된 함수를 사용하여 플러스 무한대의 극한을 계산합니다.

$\displaystyle \lim_{x \to +\infty}\frac{x^3-2x+5}{2x^3-9}= \frac{+\infty}{+\infty}=\mathbf{\frac{1}{2}}$

따라서 y=1/2 선은 함수 오른쪽의 수평 점근선입니다.

수평 점근선이란 무엇입니까?

함수의 수평 점근선을 계산하는 방법

수평 점근선 예

수평 점근선 문제 해결

연습 1

연습 2

연습 3

댓글 달기 댓글 취소