선과 평면 사이의 각도

여기에서는 선과 평면 사이의 각도를 계산하는 방법을 확인할 수 있습니다. 또한 예를 볼 수 있을 뿐만 아니라 선과 면 사이의 각도를 단계별로 해결하는 연습을 통해 연습할 수도 있습니다.

선과 평면 사이의 각도는 얼마입니까?

선과 평면 사이의 각도는 선과 평면의 직교 투영 사이의 각도입니다.

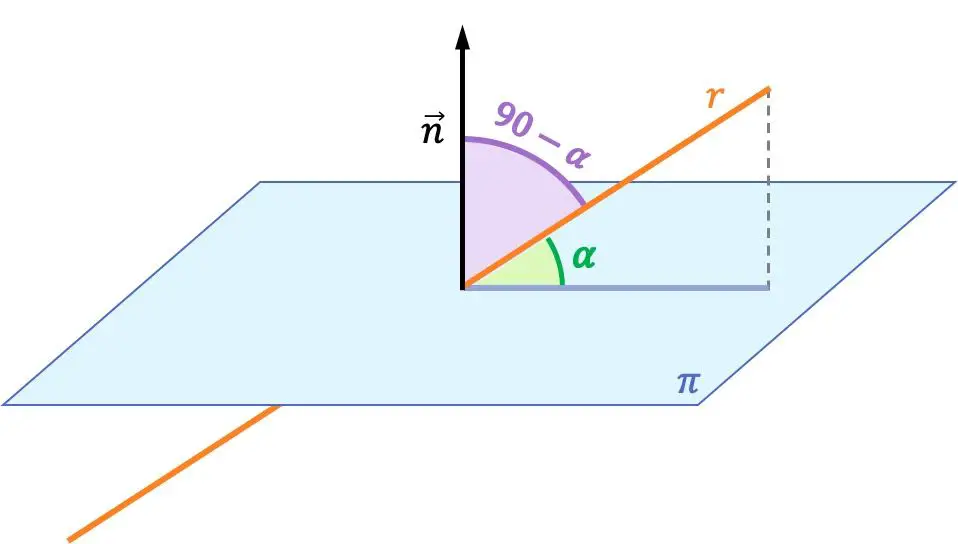
선과 평면 사이의 각도는 해당 선과 평면에 수직인 벡터 사이의 각도의 보수입니다. 따라서 선과 평면 사이의 각도는 선의 방향 벡터와 평면의 법선 벡터 사이의 각도로부터 계산됩니다.

선과 평면 사이의 각도 공식

평면과 선 사이의 각도 공식을 추론하려면 두 벡터 사이의 각도를 찾는 방법을 알아야 합니다. 링크된 페이지에는 설명은 물론 예제와 연습문제가 단계별로 풀려 있으니, 어떻게 해야 할지 기억나지 않는다면 한 번 살펴보는 것을 추천합니다.

따라서 선과 평면 사이의 각도는 해당 선의 방향 벡터 사이의 각도에 상보적이므로

$(\vv{\text{v}}_r)$

그리고 상기 평면에 대한 법선 벡터

$(\vv{n})$

, 두 벡터 사이의 각도 공식을 통해 선과 평면 사이의 각도는 다음 표현식과 동일하다고 추론합니다.

$\displaystyle \text{sen}(\alpha)=\cos(90-\alpha) =\cfrac{\lvert \vv{\text{v}}_r \cdot \vv{n} \rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

따라서 선과 평면 사이의 각도 공식은 다음과 같습니다 .

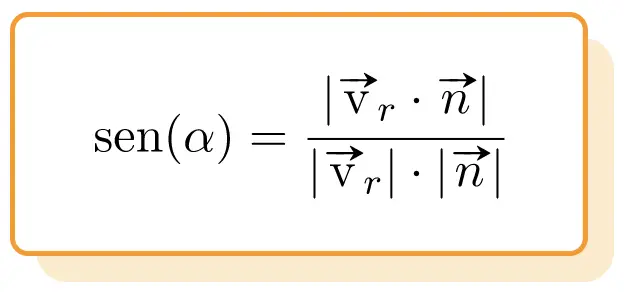
금:

$\vv{\text{v}}_r$

은 선의 직접 벡터입니다.
$\vv{n}$

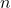
평면에 수직인 벡터입니다.

선과 평면 사이의 각도 계산 예

이러한 유형의 문제를 해결하는 방법을 볼 수 있도록 선과 평면 사이의 각도를 계산하는 예는 다음과 같습니다.

선이 이루는 각도를 계산하세요.
$r$

비행기와 함께

$\pi.$

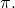
방정식은 다음과 같습니다.

$\displaystyle r: \ \begin{cases} x= 3-t \\[1.7ex] y = 2+4t \\[1.7ex] z=-3t \end{cases}\qquad\qquad \pi : \ x-y+4z+5=0$

선은 매개변수 방정식의 형태로 표현되므로 방향 벡터는 다음과 같습니다.

$\vv{\text{v}}_r = (-1,4,-3)$

반면, 평면은 암시적(또는 일반) 방정식의 형태로 정의되므로 법선 벡터는 다음과 같습니다.

$\vv{n} = (1,-1,4)$

따라서 선의 방향 벡터와 평면의 법선 벡터를 알고 나면 선과 평면 사이의 각도에 대한 공식을 적용합니다.

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

공식에서 벡터를 대체합니다.

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-1,4,-3) \cdot (1,-1,4)\rvert}{\sqrt{(-1)^2+4^2+(-3)^2} \cdot \sqrt{1^2+(-1)^2+4^2}}$

그리고 우리는 계산을 합니다:

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -1\cdot 1 +4 \cdot (-1) + (-3) \cdot 4\rvert}{\sqrt{26}\cdot \sqrt{18}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-17|}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{17}{\sqrt{468}}$

$\displaystyle \text{sen}(\alpha)= 0,79$

마지막으로 계산기를 사용하여 사인을 반전시키고 각도 값을 찾습니다.

$\alpha = \text{sen}^{-1} (0,79) = \bm{51,80º}$

따라서 선과 평면 사이의 각도는 약 51.80°입니다.

0°의 결과를 얻는다면 이는 선과 평면이 평행하거나 선이 평면에 포함되어 있음을 의미한다는 점을 고려해야 합니다. 그리고 각도가 90°이면 선과 평면이 수직임을 의미합니다.

선과 평면 사이의 각도 문제 해결

연습 1

선이 이루는 각도 구하기

$r$

비행기와 함께

$\pi.$

방정식은 다음과 같습니다.

$\displaystyle r: \ \cfrac{x-1}{2} = \cfrac{y+1}{-1} = \cfrac{z+3}{-3}$

$\displaystyle \pi : \ 3x+y+2z-1=0$

해결책 보기

선은 연속 방정식으로 표현되므로 방향 벡터는 다음과 같습니다.

$\vv{\text{v}}_r = (2,-1,-3)$

반면에 평면은 암시적(또는 일반) 방정식의 형태이므로 법선 벡터는 다음과 같습니다.

$\vv{n} = (3,1,2)$

따라서 선의 방향 벡터와 평면의 법선 벡터를 알고 나면 선과 평면 사이의 각도에 대한 공식을 사용합니다.

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(2,-1,-3) \cdot (3,1,2)\rvert}{\sqrt{2^2+(-1)^2+(-3)^2} \cdot \sqrt{3^2+1^2+2^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert 2\cdot 3 +(-1) \cdot 1 + (-3) \cdot 2\rvert}{\sqrt{14}\cdot \sqrt{14}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{|-1|}{14}$

$\displaystyle \text{sen}(\alpha) = \cfrac{1}{14}$

$\displaystyle \text{sen}(\alpha)= 0,07$

마지막으로 사인을 반전시켜 각도 값을 찾습니다.

$\alpha = \text{sen}^{-1} (0,07) = \bm{4,10º}$

따라서 선과 평면 사이의 각도는 4.10°입니다.

연습 2

선이 이루는 각도를 결정하세요.

$r$

비행기와 함께

$\pi.$

방정식은 다음과 같습니다.

$\displaystyle r: \ \begin{cases} 3x-y+4z+1=0 \\[2ex] x+2y-2z+6=0 \end{cases}$

$\displaystyle \pi : \ -4x+2y-5=0$

해결책 보기

선은 암시적(또는 일반) 방정식으로 표현되므로 선을 결정하는 2개 평면에 수직인 벡터의 벡터 곱을 계산하여 선의 방향 벡터를 찾아야 합니다.

$\displaystyle\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -1 & 4 \\[1.1ex] 1 &2&-2 \end{vmatrix} = -6\vv{i}+10\vv{j}+7\vv{k}$

$\vv{\text{v}}_r = (-6,10,7)$

반면에 평면에 수직인 벡터는 다음과 같습니다.

$\vv{n} = (-4,2,0)$

따라서 선의 방향 벡터와 평면의 법선 벡터를 알고 나면 선과 평면 사이의 각도에 대한 공식을 사용합니다.

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle\text{sen}(\alpha) =\cfrac{\lvert(-6,10,7) \cdot (-4,2,0)\rvert}{\sqrt{(-6)^2+10^2+7^2} \cdot \sqrt{(-4)^2+2^2+0^2}}$

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert -6\cdot (-4) +10 \cdot 2 + 7 \cdot 0\rvert}{\sqrt{185}\cdot \sqrt{20}}$

$\displaystyle \text{sen}(\alpha) = \cfrac{44}{\sqrt{3700}}$

$\displaystyle \text{sen}(\alpha)= 0,72$

마지막으로 사인을 반전시켜 각도 값을 찾습니다.

$\alpha = \text{sen}^{-1} (0,72) = \bm{46,33º}$

따라서 선과 평면 사이의 각도는 46.33°입니다.

연습 3

선과 평면 사이의 각도 공식을 사용하여 다음 값을 구합니다.

$k$

권리를 위해 꼭 필요한

$r$

그리고 비행기

$\pi$

평행해지세요.

$\displaystyle r: \ (x,y,z) = (2,0-1)+t(4,-1,3)$

$\displaystyle \pi : \ 4x+3y+kz+7=0$

해결책 보기

먼저 선은 벡터 방정식으로 표현되므로 방향 벡터는 다음과 같습니다.

$\vv{\text{v}}_r = (4,-1,3)$

반면에 평면은 일반 방정식의 형태이므로 법선 벡터는 다음과 같습니다.

$\vv{n} = (4,3,k)$

따라서 두 기하학적 요소가 평행하려면 두 요소 사이의 각도가 0이어야 합니다. 따라서 선과 평면 사이의 각도 공식은 다음과 같습니다.

$\displaystyle \text{sen}(\alpha) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle \text{sen}(0º) =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 =\cfrac{\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert}{\lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert}$

$\displaystyle 0 \cdot \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{n} \rvert =\lvert\vv{\text{v}}_r \cdot \vv{n}\rvert$

$\displaystyle 0 =\vv{\text{v}}_r \cdot \vv{n}$

따라서 선의 방향 벡터와 법선 벡터 사이의 내적은 0이어야 합니다. 그리고 이 방정식으로부터 우리는 미지의 값을 결정할 수 있습니다.

$k:$

$\displaystyle 0 =(4,-1,3) \cdot (4,3,k)$

$\displaystyle 0 =4\cdot 4 -1\cdot 3 +3 \cdot k$

$\displaystyle 0 =16 -3 +3 k$

$\displaystyle -3k =13$

$\displaystyle k =\cfrac{13}{-3}$

$\displaystyle \bm{k =-}\mathbf{\cfrac{13}{3}}$

마지막으로, 이 기사가 도움이 되었다면 아마도 두 평면 사이의 각도를 찾는 방법에도 관심이 있을 것입니다. 링크 페이지에서는 서로 다른 두 평면 사이의 각도를 계산하는 데 필요한 공식뿐만 아니라 매우 자세한 설명을 찾을 수 있으며, 또한 연습하고 이해할 수 있도록 단계별로 해결되는 예와 연습을 볼 수 있습니다. 어떻게 하면 완벽하게 이루어지는지.

선과 평면 사이의 각도는 얼마입니까?

선과 평면 사이의 각도 공식

선과 평면 사이의 각도 계산 예

선과 평면 사이의 각도 문제 해결

연습 1

연습 2

연습 3

댓글 달기 댓글 취소