이 페이지에서는 선과 원 사이에 존재하는 다양한 상대 위치에 대해 설명합니다. 또한 선과 원 사이의 상대적 위치를 찾는 방법을 볼 수 있습니다.
선과 원의 상대적인 위치는 무엇입니까?
분석 기하학에서 원에 대한 선의 상대 위치는 외부, 접선 또는 할선만 될 수 있습니다.
- 외부 : 선과 원의 중심 사이의 거리가 반경보다 큰 경우.
- 접선(Tangent) : 선과 원의 중심 사이의 거리가 반지름과 같은 경우.
- 시컨트(Secant) : 선과 원의 중심 사이의 거리가 반지름보다 작은 경우.
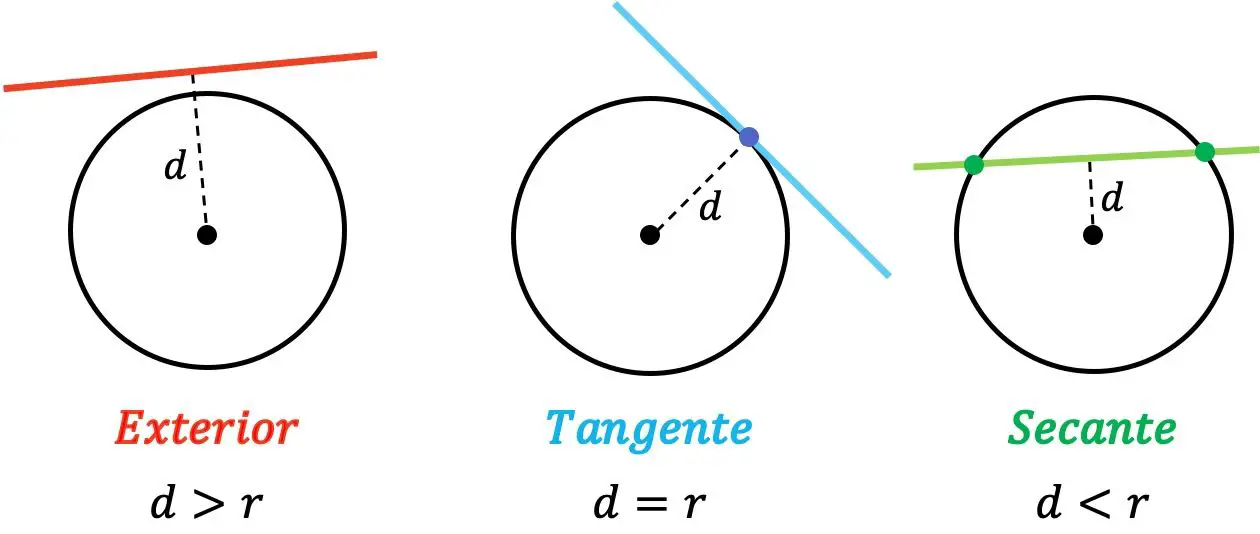
따라서 선이 원 외부에 있으면 어떤 지점에서도 교차하지 않습니다. 반면에 선이 원에 접할 때 두 선에는 공통점이 있습니다. 그리고 마지막으로, 선은 두 개의 서로 다른 점에서 교차할 때 원에 분할됩니다.
선과 원 사이의 상대적 위치를 결정하는 방법은 무엇입니까?
평면에서 원에 대한 선의 상대적 위치를 찾는 방법에는 두 가지가 있습니다. 하나는 선과 원 중심 사이의 거리를 계산하는 것이고, 다른 하나는 방정식의 복합 방정식을 푸는 것입니다. 선과 원의 방정식.
다음으로 각 방법이 정확히 무엇인지 살펴보겠습니다.
방법 1: 선과 원 중심 사이의 거리
선과 원의 상대위치 개념 설명에서 보았듯이, 선과 원의 중심 사이의 거리가 어떤 상대위치인지를 나타낸다.
따라서 이 방법은 선과 원 중심 사이의 거리를 찾는 것으로 구성됩니다. 분명히, 그것을 할 수 있으려면 점과 선 사이의 거리를 계산하는 방법을 알아야 합니다. 이 페이지에서는 그 방법을 볼 수 있을 뿐만 아니라 연습할 예제와 해결된 연습 문제도 볼 수 있습니다.
따라서 얻은 거리의 결과에 따라 다음과 같은 경우가 됩니다.
- 얻은 거리가 원의 반경보다 크면 선은 원 외부에 있게 됩니다.
- 얻은 거리가 원의 반지름과 같으면 선은 원에 접하게 됩니다.
- 얻은 거리가 원의 반지름보다 작으면 선은 원과 교차합니다.
방법 2: 연립방정식 풀기
원에 대한 선의 상대적 위치를 찾는 또 다른 방법은 선의 방정식과 원의 방정식으로 구성된 방정식 시스템을 사용하는 것입니다. 분명히, 이 방법을 적용하려면 원주 방정식이 무엇인지 , 선 방정식의 공식이 무엇인지 알아야 합니다.
방정식 시스템의 해 수에 따라 우리는 다음과 같은 경우에 직면하게 됩니다.
- 연립방정식 에 해가 없다는 것은 선과 원이 공통점을 갖지 않으므로 선이 원 밖에 있다는 뜻입니다.
- 연립 방정식의 해가 1개인 경우 이는 선과 원이 공통점을 갖고 있으므로 선이 원에 접한다 는 것을 의미합니다.
- 연립방정식 에 2개의 해가 있는 경우 이는 선과 원이 두 개의 공통 점을 갖고 있으므로 선이 원에 이등분 된다는 의미입니다.